Logistic mixed-effects regression

Martijn Wieling (University of Groningen)

This lecture

Introduction
- Gender processing in Dutch
- Eye-tracking to reveal gender processing
Design
Analysis: logistic mixed-effects regression
Conclusion

Gender processing in Dutch

Study’s goal: assess if Dutch people use grammatical gender to anticipate upcoming words
This study was conducted together with Hanneke Loerts and is published in the Journal of Psycholinguistic Research (Loerts, Wieling and Schmid, 2012)
What is grammatical gender?
- Gender is a property of a noun
- Nouns are divided into classes: masculine, feminine, neuter, …
- E.g., hond (‘dog’) = common (masculine/feminine), paard (‘horse’) = neuter
The gender of a noun can be determined from the forms of elements syntactically related to it

Gender in Dutch

Gender in Dutch: 70% common, 30% neuter
When a noun is diminutive it is always neuter (the Dutch often use diminutives!)
Gender is unpredictable from the root noun and hard to learn

Why use eye tracking?

Eye tracking reveals incremental processing of the listener during time course of speech signal
As people tend to look at what they hear (Cooper, 1974), lexical competition can be tested

Testing lexical competition using eye tracking

Cohort Model (Marslen-Wilson & Welsh, 1978): competition between words is based on word-initial activation

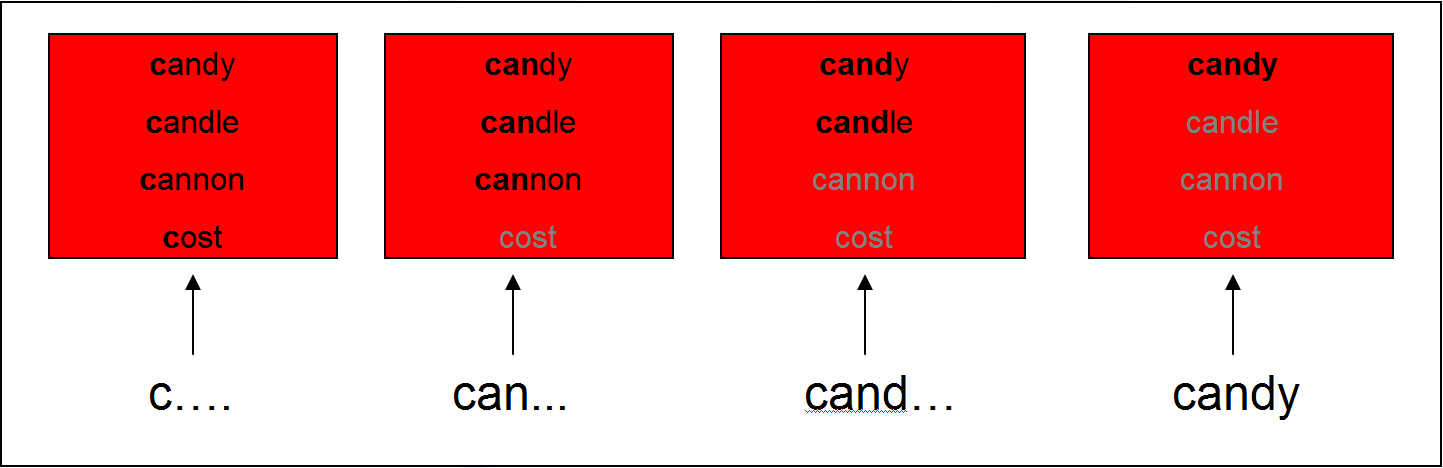
This can be tested using the visual world paradigm: following eye movements while participants receive auditory input to click on one of several objects on a screen

Support for the Cohort Model

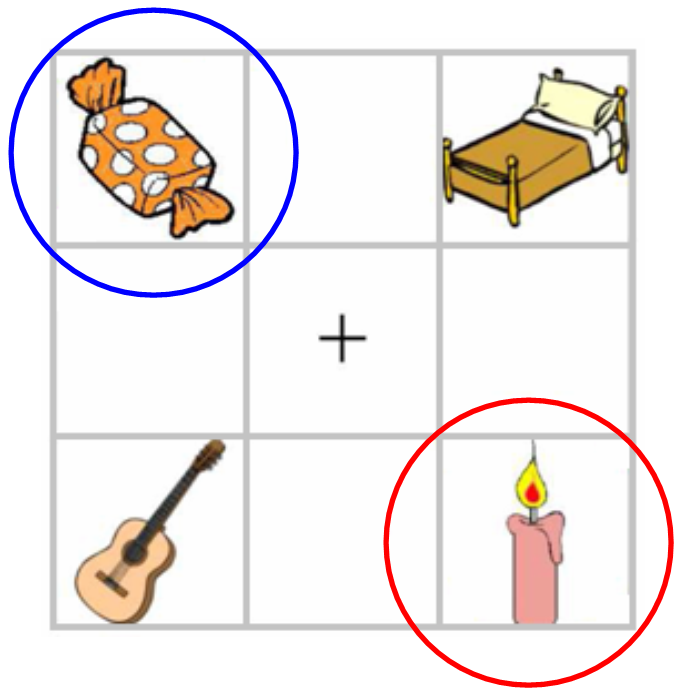
Subjects hear: “Pick up the candy” (Tanenhaus et al., 1995)
Fixations towards target (Candy) and competitor (Candle): support for the Cohort Model

Lexical competition based on syntactic gender

Other models of lexical processing state that lexical competition occurs based on all acoustic input (e.g., TRACE, Shortlist, NAM)
Does syntactic gender information restrict the possible set of lexical candidates?
- If you hear de, do you focus more on de hond (dog) than on het paard (horse)?
- Previous studies (e.g., Dahan et al., 2000 for French) have indicated gender information restricts the possible set of lexical candidates
We will investigate if this also holds for Dutch (other gender system) via the VWP
We analyze the data using (generalized) linear mixed-effects regression in R

Experimental design

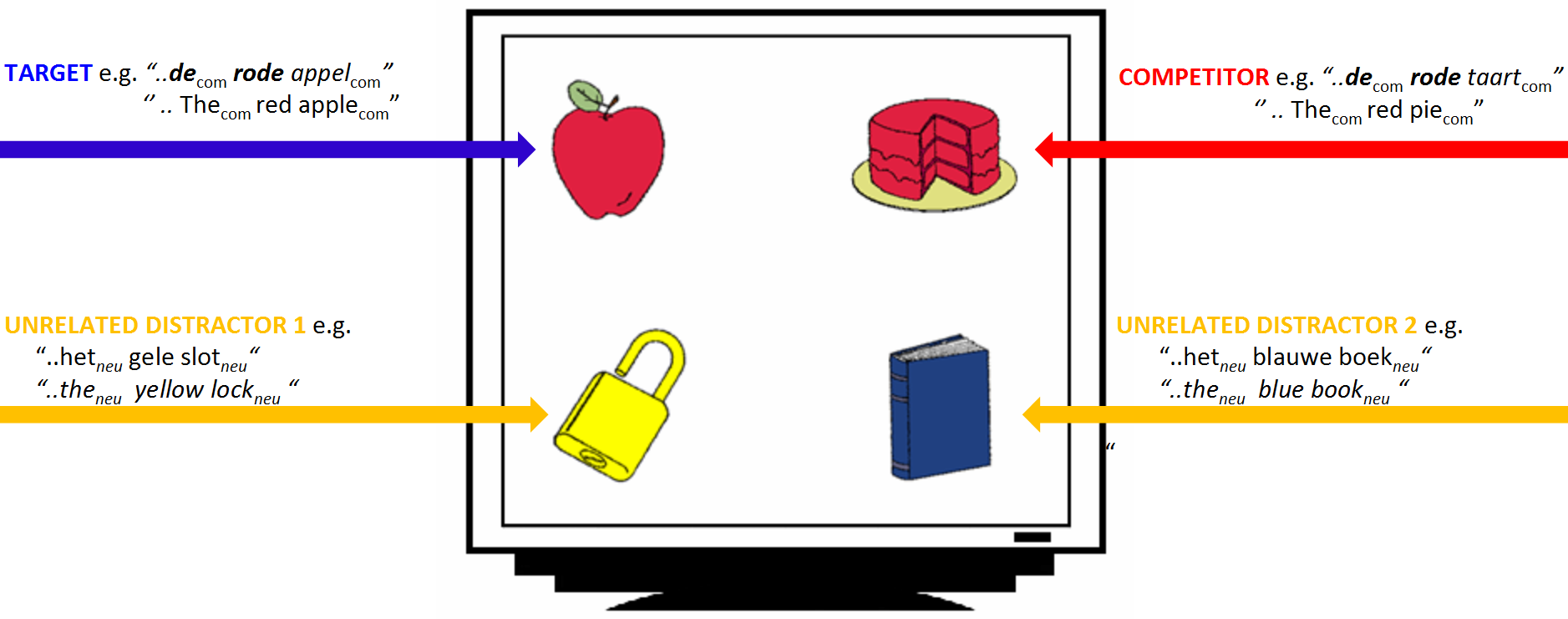
28 Dutch participants heard sentences like:
Klik op de rode appel (‘click on the red apple’)
Klik op het plaatje met een blauw boek (‘click on the image of a blue book’)
They were shown 4 nouns varying in color and gender
Eye movements were tracked with a Tobii eye-tracker (E-Prime extensions)

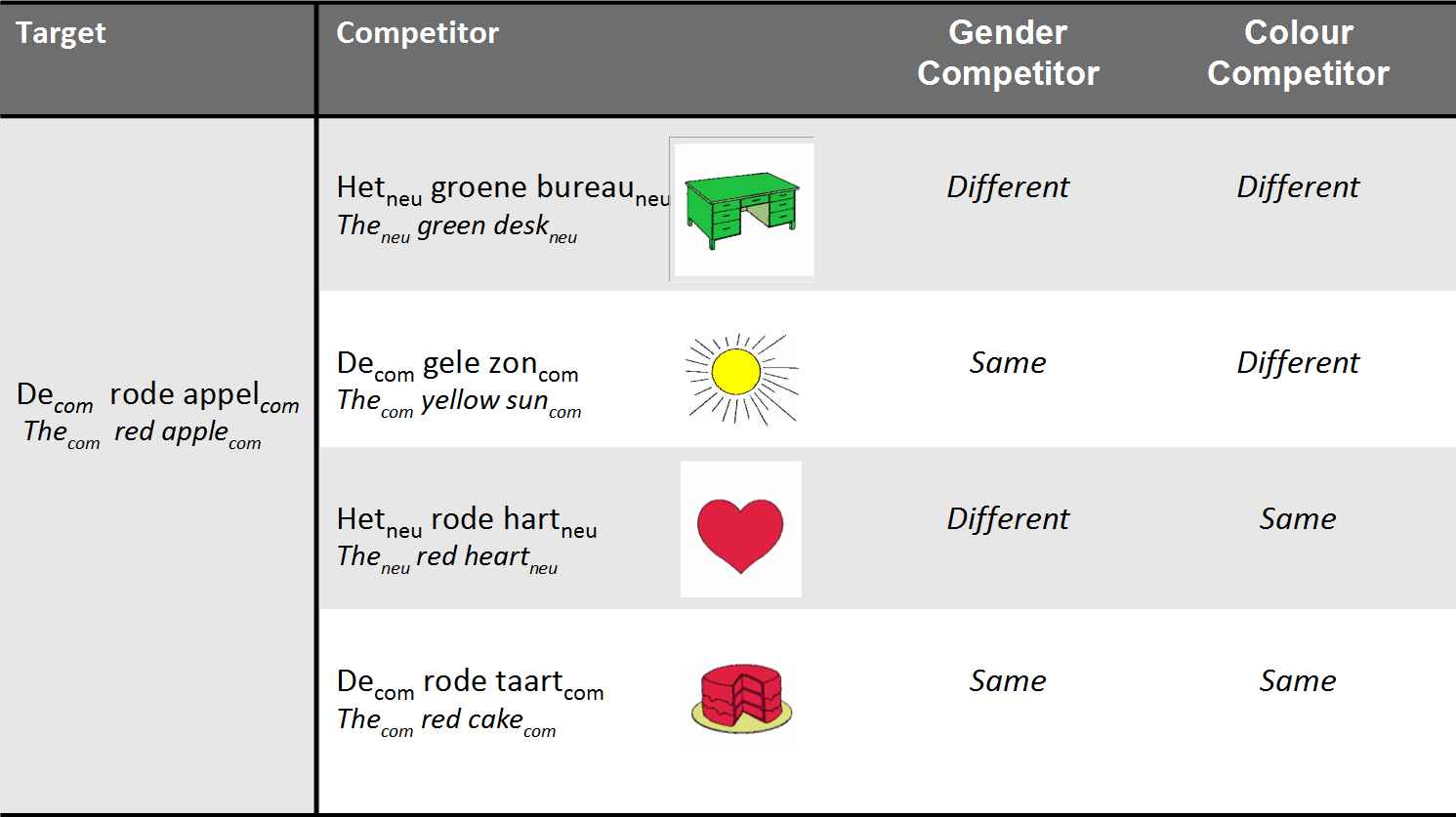
Experimental design: conditions

Subjects were shown 96 different screens
48 screens for indefinite sentences (“Klik op het plaatje met een rode appel.”)
48 screens for definite sentences (“Klik op de rode appel.”)

Visualizing fixation proportions: different color

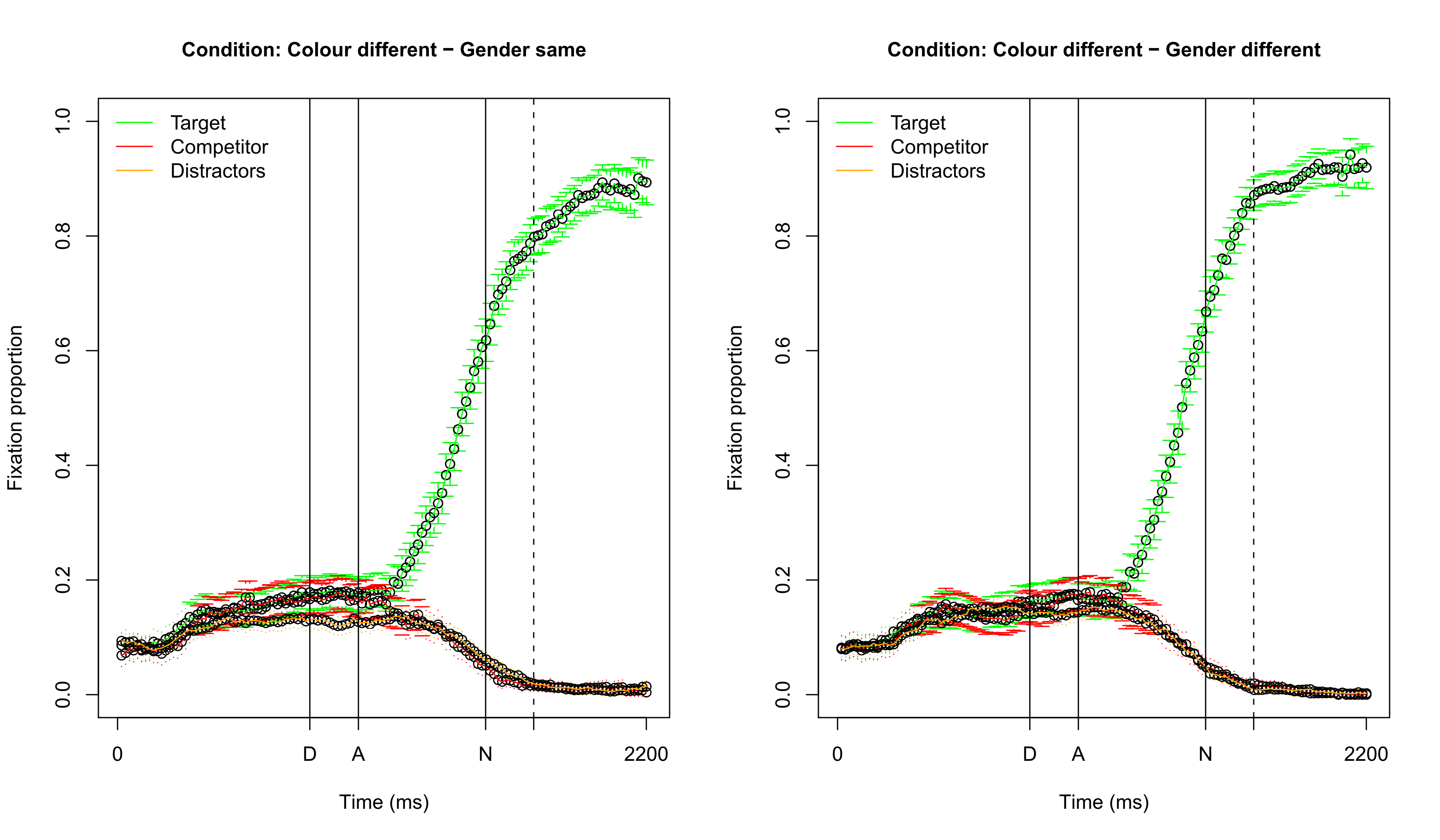
Visualizing fixation proportions: same color

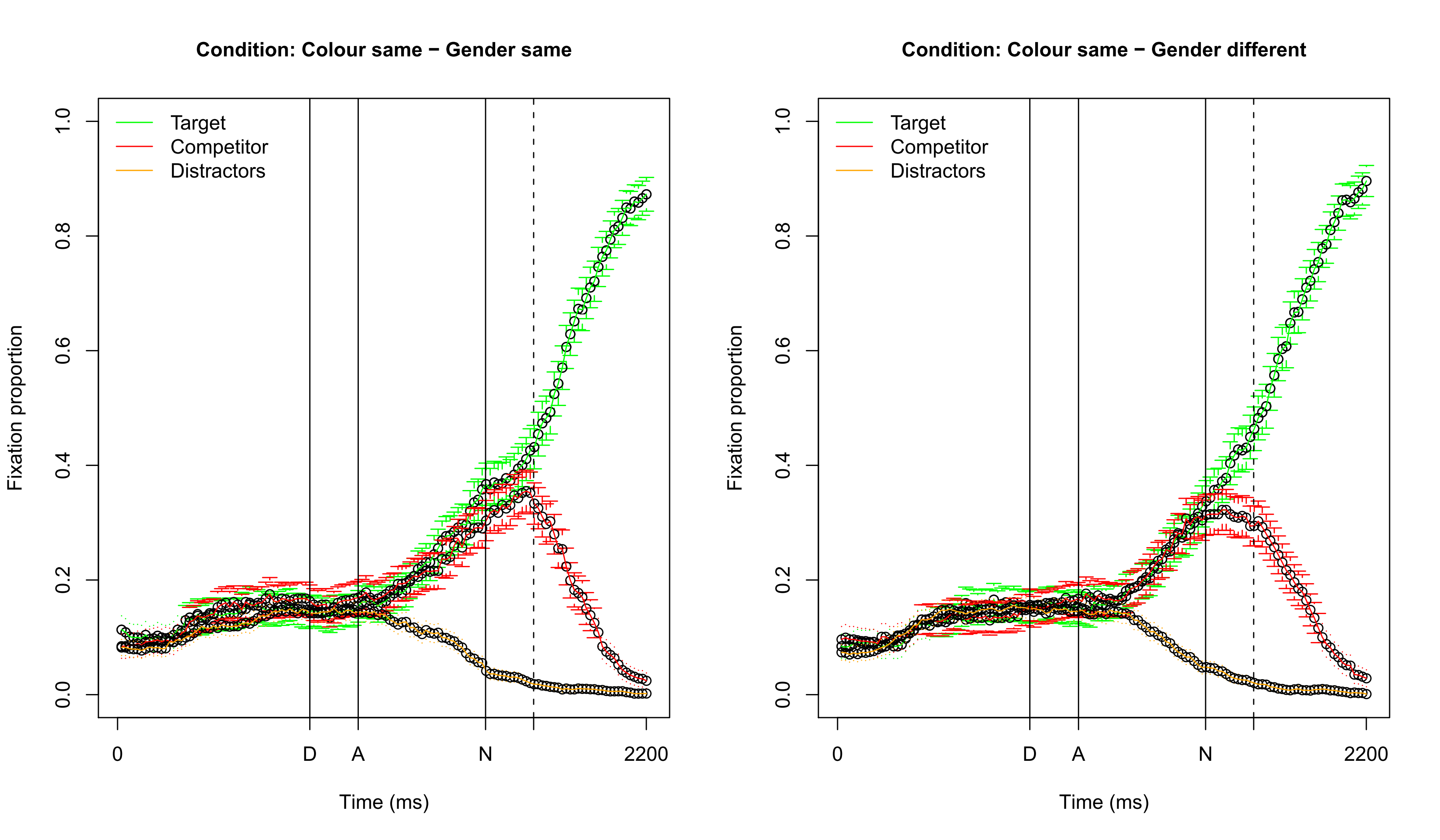
Which dependent variable? (1)

Difficulty 1: choosing the dependent variable
- Fixation difference between target and competitor
- Fixation proportion on target: requires transformation to empirical logit, to ensure the dependent variable is unbounded: \(\log( \frac{(y + 0.5)}{(N - y + 0.5)} )\)
- Logistic regression comparing fixations on target versus competitor
Difficulty 2: selecting a time span to average over
- Note that about 200 ms. is needed to plan and launch an eye movement
- It is possible (and better) to take every individual sampling point into account, but we will opt for the simpler approach here (in contrast to the GAM approach)

Question 1

Which dependent variable? (2)

Here we use logistic mixed-effects regression comparing fixations on the target versus the competitor
Averaged over the time span starting 200 ms. after the onset of the determiner and ending 200 ms. after the onset of the noun (about 800 ms.)
This ensures that gender information has been heard and processed, both for the definite and indefinite sentences

Generalized linear mixed-effects regression

A generalized linear (mixed-effects) regression model (GLM) is a generalization of linear (mixed-effects) regression model
- Response variables may have an error distribution different than the norm. dist.
- Linear model is related to response variable via link function
- Variance of measurements may depend on the predicted value
Examples of GLMs are Poisson regression, logistic regression, etc.

Logistic (mixed-effects) regression

Dependent variable is binary (1: success, 0: failure): modeled as probabilities
Transform to continuous variable via log odds link function: \(\log(\frac{p}{1-p}) = \textrm{logit}(p)\)
- In R: logit(p) (from library car)
Interpret coefficients w.r.t. success as logits (in R: plogis(x))

Logistic mixed-effects regression: assumptions

Independent observations within each level of the random-effect factor
Relation between logit-transformed DV and independent variables linear
No strong multicollinearity
No highly influential outliers (i.e. assessed using model criticism)
Important: No normality or homoscedasticity assumptions about the residuals

Some remarks about data preparation

Check pairwise correlations of your predictor variables
- If high: exclude variable / combine variables (residualization is not OK)
- See also: Chapter 6.2.2 of Baayen (2008)
Check distribution of numerical predictors
- If skewed, it may help to transform them
Center your numerical predictors when doing mixed-effects regression

Our study: independent variables (1)

Variable of interest:
- Competitor gender vs. target gender
Variables which are/could be important:
- Competitor vs. target color
- Gender of target (common or neuter)
- Definiteness of target

Our study: independent variables (2)

Participant-related variables:
- Sex (male/female), age, education level
- Trial number
Design control variables:
- Competitor position vs. target position (up-down or down-up)
- Color of target
- … (anything else you are not interested in, but potentially problematic)

Question 2

Dataset

head(eye)

  Subject   Item TargetDefinite TargetNeuter TargetColor TargetPlace CompColor
1    S300   boom              1            0       green           3     brown
2    S300  bloem              1            0         red           4     green
3    S300  anker              1            1      yellow           3    yellow
4    S300   auto              1            0       green           3     brown
5    S300   boek              1            1        blue           4      blue
6    S300 varken              1            1       brown           1     green
  CompPlace TrialID Age IsMale Edulevel SameColor SameGender TargetFocus CompFocus
1         2       1  52      0        1         0          1          43        41
2         2       2  52      0        1         0          0         100         0
3         2       3  52      0        1         1          1          73        27
4         2       4  52      0        1         0          0         100         0
5         3       5  52      0        1         1          0          12        21
6         3       6  52      0        1         0          0           0        51

Our first generalized mixed-effects regression model

(R version 4.5.0 (2025-04-11 ucrt), `lme4` version 1.1.37)

library(lme4)
model1 <- glmer( cbind(TargetFocus, CompFocus) ~ (1|Subject) + (1|Item), 
                 data=eye, family='binomial' ) # intercept-only model
summary(model1) # slides only show relevant part of the summary

Random effects:
 Groups  Name        Std.Dev.
 Item    (Intercept) 0.326   
 Subject (Intercept) 0.588   

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)    0.848      0.121    7.02 2.28e-12 ***

Interpreting logit coefficients I

fixef(model1) # show fixed effects

(Intercept) 
      0.848

plogis( fixef(model1)["(Intercept)"] )

(Intercept) 
        0.7

On average 70% chance to focus on target

By-item random intercepts

By-subject random intercepts

Is a by-item analysis necessary?

model0 <- glmer( cbind(TargetFocus, CompFocus) ~ (1|Subject), data=eye, family='binomial')
anova(model0,model1) # random intercept for item is necessary

Data: eye
Models:
model0: cbind(TargetFocus, CompFocus) ~ (1 | Subject)
model1: cbind(TargetFocus, CompFocus) ~ (1 | Subject) + (1 | Item)
       npar    AIC    BIC logLik -2*log(L) Chisq Df Pr(>Chisq)    
model0    2 128304 128315 -64150    128300                        
model1    3 125387 125404 -62690    125381  2919  1     <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Only fitting method available for glmer is ML (i.e. refit in anova unnecessary)

Adding a fixed-effect predictor

model2 <- glmer( cbind(TargetFocus, CompFocus) ~ SameColor + (1|Subject) + (1|Item), 
                 data=eye, family='binomial')
summary(model2)$coef # show only fixed effects

            Estimate Std. Error z value Pr(>|z|)    
(Intercept)     1.68     0.1209    13.9   <2e-16 ***
SameColor      -1.48     0.0118  -125.5   <2e-16 ***

We start with SameColor as this effect will be the most dominant
Significant negative estimate: less likely to focus on target
We need to test if the effect of SameColor varies per subject
- If there is much between-subject variation, this will influence signficance

Testing for a random slope

model3 <- glmer( cbind(TargetFocus, CompFocus) ~ SameColor + (1+SameColor|Subject) + (1|Item), data=eye, 
                 family='binomial') # always: (1 + factorial predictor | ranef)
anova(model2,model3)$P[2] # random slope necessary (p-value is so low that R shows 0)

[1] 0

summary(model3)

Random effects:
 Groups  Name        Std.Dev. Corr 
 Item    (Intercept) 0.359         
 Subject (Intercept) 1.251         
         SameColor   0.949    -0.95

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)     1.89      0.245    7.69 1.45e-14 ***
SameColor      -1.71      0.184   -9.29   <2e-16 ***

Investigating the gender effect (hypothesis test)

model4 <- glmer( cbind(TargetFocus, CompFocus) ~ SameColor + SameGender + (1+SameColor|Subject) + (1|Item), 
                 data=eye, family='binomial')
summary(model4)$coef

            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   1.8536     0.2463    7.53  5.2e-14 ***
SameColor    -1.7124     0.1847   -9.27   <2e-16 ***
SameGender    0.0742     0.0115    6.47 9.97e-11 ***

It seems the gender is effect is opposite to our expectations…
Perhaps there is an effect of common vs. neuter gender?

Visualizing fixation proportions: common (OK)

Visualizing fixation proportions: neuter (not OK)

Adding the contrast between common and neuter

(from now on: exploratory analysis)

model5 <- glmer( cbind(TargetFocus, CompFocus) ~ SameColor + SameGender + TargetNeuter + 
                   (1+SameColor|Subject) + (1|Item), data=eye, family='binomial')
summary(model5)$coef # contrast is not significant

             Estimate Std. Error z value Pr(>|z|)    
(Intercept)    1.9398     0.2509    7.73 1.07e-14 ***
SameColor     -1.7125     0.1845   -9.28   <2e-16 ***
SameGender     0.0742     0.0115    6.47 9.92e-11 ***
TargetNeuter  -0.1723     0.1015   -1.70    0.090

anova(model4,model5)$P[2] # noun type contrast by itself is not needed in a better model

[1] 0.0944

Testing the interaction

model6 <- glmer( cbind(TargetFocus, CompFocus) ~ SameColor + SameGender * TargetNeuter + 
                   (1+SameColor|Subject) + (1|Item), data=eye, family='binomial')
summary(model6)$coef

                        Estimate Std. Error z value Pr(>|z|)    
(Intercept)                2.067     0.2515    8.22 2.01e-16 ***
SameColor                 -1.716     0.1848   -9.29   <2e-16 ***
SameGender                -0.174     0.0164  -10.63   <2e-16 ***
TargetNeuter              -0.416     0.1026   -4.05 5.13e-05 ***
SameGender:TargetNeuter    0.487     0.0230   21.24   <2e-16 ***

anova(model4,model6)$P[2]

[1] 1.74e-99

There is clear support for an interaction between noun type and gender condition

Visualizing the interaction: interpretation

par(mfrow=c(1,2))
visreg(model6, "SameGender", by="TargetNeuter", overlay=T) # from library(visreg)
visreg(model6, "SameGender", by="TargetNeuter", overlay=T, trans=plogis)

Common noun pattern as expected, but neuter noun pattern inverted
- Unfortunately, we have no sensible explanation for this finding

Example of adding a multilevel factor to the model

eye$TargetColor <- relevel( eye$TargetColor, "brown" ) # set specific reference level
model7 <- glmer( cbind(TargetFocus, CompFocus) ~ SameColor + SameGender * TargetNeuter + 
                   TargetColor + (1+SameColor|Subject) + (1|Item), data=eye, family='binomial')
summary(model7)$coef # inclusion warranted (anova: p = 0.005; not shown)

                        Estimate Std. Error z value Pr(>|z|)    
(Intercept)                1.707     0.2669    6.40 1.58e-10 ***
SameColor                 -1.716     0.1847   -9.29   <2e-16 ***
SameGender                -0.174     0.0164  -10.63   <2e-16 ***
TargetNeuter              -0.415     0.0880   -4.72 2.33e-06 ***
TargetColorblue            0.275     0.1433    1.92    0.055    
TargetColorgreen           0.494     0.1434    3.44 0.000574 ***
TargetColorred             0.456     0.1433    3.18    0.001 ** 
TargetColoryellow          0.502     0.1433    3.50 0.000464 ***
SameGender:TargetNeuter    0.488     0.0230   21.24   <2e-16 ***

Comparing different factor levels

summary(glht(model7,linfct=mcp(TargetColor = "Tukey"))) # from library(multcomp)


     Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: glmer(formula = cbind(TargetFocus, CompFocus) ~ SameColor + SameGender * 
    TargetNeuter + TargetColor + (1 + SameColor | Subject) + 
    (1 | Item), data = eye, family = "binomial")

Linear Hypotheses:
                    Estimate Std. Error z value Pr(>|z|)   
blue - brown == 0    0.27510    0.14329    1.92   0.3063   
green - brown == 0   0.49377    0.14339    3.44   0.0052 **
red - brown == 0     0.45611    0.14328    3.18   0.0126 * 
yellow - brown == 0  0.50162    0.14329    3.50   0.0041 **
green - blue == 0    0.21867    0.13516    1.62   0.4855   
red - blue == 0      0.18101    0.13506    1.34   0.6657   
yellow - blue == 0   0.22653    0.13506    1.68   0.4478   
red - green == 0    -0.03766    0.13516   -0.28   0.9987   
yellow - green == 0  0.00786    0.13517    0.06   1.0000   
yellow - red == 0    0.04551    0.13506    0.34   0.9972   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Adjusted p values reported -- single-step method)

Simplifying the factor in a contrast

eye$TargetBrown <- (eye$TargetColor == "brown")*1
model8 <- glmer( cbind(TargetFocus, CompFocus) ~ SameColor + SameGender * TargetNeuter + TargetBrown + 
                   (1+SameColor|Subject) + (1|Item), data=eye, family='binomial')
summary(model8)$coef

                        Estimate Std. Error z value Pr(>|z|)    
(Intercept)                2.139     0.2502    8.55   <2e-16 ***
SameColor                 -1.716     0.1849   -9.29   <2e-16 ***
SameGender                -0.174     0.0164  -10.63   <2e-16 ***
TargetNeuter              -0.415     0.0913   -4.55 5.36e-06 ***
TargetBrown               -0.432     0.1215   -3.55 0.000382 ***
SameGender:TargetNeuter    0.488     0.0230   21.24   <2e-16 ***

anova(model8,model7)$P[2] # N.B. model7 is more complex: model with TargetBrown preferred

[1] 0.311

Interpreting logit coefficients II

# chance to focus on target when there is a color competitor and 
# a gender competitor, while the target is common and not brown
(logit <- fixef(model8)["(Intercept)"] + 1 * fixef(model8)["SameColor"] + 
         1 * fixef(model8)["SameGender"] + 0 * fixef(model8)["TargetNeuter"] + 
         0 * fixef(model8)["TargetBrown"] + 
         1 * 0 * fixef(model8)["SameGender:TargetNeuter"])

(Intercept) 
      0.248

plogis(logit) # intercept-only model was 0.7

(Intercept) 
      0.562

Distribution of residuals

qqnorm( resid( model8 ) )
qqline( resid( model8 ) )

Not normal, but also not required for logistic regression

Model criticism: effect of excluding outliers

eye2 <- eye[abs(scale(resid(model8))) < 2,] # 97% of original data included
model8b <- glmer( cbind(TargetFocus, CompFocus) ~ SameColor + SameGender * TargetNeuter + TargetBrown + 
                    (1+SameColor|Subject) + (1|Item), data=eye2, family='binomial')
summary(model8b)$coef

                        Estimate Std. Error z value Pr(>|z|)    
(Intercept)                2.582     0.3325    7.77 8.15e-15 ***
SameColor                 -1.803     0.2043   -8.82   <2e-16 ***
SameGender                -0.269     0.0174  -15.39   <2e-16 ***
TargetNeuter              -0.514     0.1181   -4.35 1.37e-05 ***
TargetBrown               -0.602     0.1576   -3.82 0.000133 ***
SameGender:TargetNeuter    0.701     0.0244   28.78   <2e-16 ***

Results remain largely the same: no undue influence of outliers!

Question 3

Many more things to do…

We still need to:
- See if the significant fixed effects remain significant when adding the (necessary) random slopes
- See (in this exploratory analysis phase) if there are other variables we should include (e.g., education level)
- See if there are other interactions which should be included
- Apply model criticism after these steps
In the associated lab session, these issues are discussed:
- A subset of the data is used (only same color)
- Simple R-functions are provided to generate all plots

Recap

We have learned how to create logistic mixed-effects regression models
We have learned how to interpret the results (in terms of logits)
However, we analyzed this data in a non-optimal way:
- It would be better to predict target focus for every timepoint (GAMs!)
Associated lab session:
- https://www.let.rug.nl/wieling/Statistics/Logistic-Mixed-Effects/lab

Evaluation

Questions?

Thank you for your attention!

https://www.martijnwieling.nl

m.b.wieling@rug.nl

Logistic mixed-effects regression

This lecture

Gender processing in Dutch

Gender in Dutch

Why use eye tracking?

Testing lexical competition using eye tracking

Support for the Cohort Model

Lexical competition based on syntactic gender

Experimental design

Experimental design: conditions

Visualizing fixation proportions: different color

Visualizing fixation proportions: same color

Which dependent variable? (1)

Question 1

Which dependent variable? (2)

Generalized linear mixed-effects regression

Logistic (mixed-effects) regression

Logistic mixed-effects regression: assumptions

Some remarks about data preparation

Our study: independent variables (1)

Our study: independent variables (2)

Question 2

Dataset

Our first generalized mixed-effects regression model

(R version 4.5.0 (2025-04-11 ucrt), lme4 version 1.1.37)

Interpreting logit coefficients I

By-item random intercepts

By-subject random intercepts

Is a by-item analysis necessary?

Adding a fixed-effect predictor

Testing for a random slope

Investigating the gender effect (hypothesis test)

Visualizing fixation proportions: common (OK)

Visualizing fixation proportions: neuter (not OK)

Adding the contrast between common and neuter

(from now on: exploratory analysis)

Testing the interaction

Visualizing the interaction: interpretation

Example of adding a multilevel factor to the model

Comparing different factor levels

Simplifying the factor in a contrast

Interpreting logit coefficients II

Distribution of residuals

Model criticism: effect of excluding outliers

Question 3

Many more things to do…

Recap

Evaluation

Questions?

(R version 4.5.0 (2025-04-11 ucrt), `lme4` version 1.1.37)