Mixed-effects regression

Martijn Wieling (University of Groningen)

This lecture

Introduction
Recap: multiple regression
Mixed-effects regression analysis: explanation
Case-study: Influence of alcohol on L1 & L2
Conclusion

Introduction

Consider the following situation (taken from Clark, 1973):
- Mr. A and Mrs. B study reading latencies of verbs and nouns
- Each randomly selects 20 words and tests 50 subjects
- Mr. A finds (using a sign test) verbs to have faster responses
- Mrs. B finds nouns to have faster responses
How is this possible?

The language-as-fixed-effect fallacy

The problem is that Mr. A and Mrs. B disregard the (huge) variability in the words
- Mr. A included a difficult noun, but Mrs. B included a difficult verb
- Their set of words does not constitute the complete population of nouns and verbs, therefore their results are limited to their words
This is known as the language-as-fixed-effect fallacy (LAFEF)
- Fixed-effect factors have repeatable and a small number of levels
- Word is a random-effect factor (a non-repeatable random sample from a larger population)

Why linguists are not always good statisticians

LAFEF occurs frequently in linguistic research until the 1970’s
- Many reported significant results are wrong (the method is anti-conservative)!
Clark (1973) combined a by-subject (\(F_1\)) analysis and by-item (\(F_2\)) analysis in measure min F’
- Results are significant and generalizable across subjects and items when min F’ is significant
- Unfortunately many researchers (>50%!) incorrectly interpreted this study and may report wrong results (Raaijmakers et al., 1999)
- E.g., they only use \(F_1\) and \(F_2\) and not min F’ or they use \(F_2\) while unneccesary (e.g., counterbalanced design)

Our problems solved…

Apparently, analyzing this type of data is difficult…
Fortunately, using mixed-effects regression models solves these problems!
- The method is easier than using the approach of Clark (1973)
- Results can be generalized across subjects and items
- Mixed-effects models are robust to missing data (Baayen, 2008, p. 266)
- We can easily test if it is necessary to treat item as a random effect
- No balanced design necessary (as in repeated-measures ANOVA)!
But first some words about regression…

Recap: multiple regression (1)

Multiple regression: predict one numerical variable on the basis of other independent variables (numerical or categorical)
We can write a regression formula as \(y = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \epsilon\)
- \(y\): (value of the) dependent variable
- \(x_i\): (value of the) predictor
- \(\beta_0\): intercept, value of \(y\) when all \(x_i = 0\)
- \(\beta_i\): slope, change in \(y\) when the value of \(x_i\) increases with 1
- \(\epsilon\): residuals, difference between observed values and predicted (fitted) values

Recap: multiple regression (2)

Factorial predictors are (automatically) represented by binary-valued predictors: \(x_i = 0\) (reference level) or \(x_i = 1\) (alternative level)
- Factor with \(n\) levels: \(n-1\) binary predictors
- Interpretation of factorial \(\beta_i\): change from reference to alternative level
Example of regression formula:
- Predict the reaction time of a subject on the basis of word frequency, word length, and subject age: RT = 200 - 5WF + 3WL + 10SA

Mixed-effects regression modeling: introduction

Mixed-effects regression distinguishes fixed effects and random-effect factors
Fixed effects:
- All numerical predictors
- Factorial predictors with a repeatable and small number of levels (e.g., Sex)
Random-effect factors:
- Only factorial predictors!
- Levels are a non-repeatable random sample from a larger population
- Generally a large number of levels (e.g., Subject, Item)

What are random-effects factors?

Random-effect factors are factors which are likely to introduce systematic variation (here: subject and item)
- Some subjects have a slow response (RT), while others are fast
  = Random Intercept for Subject (i.e. \(\beta_0\) varies per subject)
- Some items are easy to recognize, others hard
  = Random Intercept for Item (i.e. \(\beta_0\) varies per item)
- The effect of item frequency on RT might be higher for one subject than another: e.g., non-native participants might benefit more from frequent words than native participants
  = Random Slope for Item Frequency per Subject (i.e. \(\beta_{\textrm{WF}}\) varies per subject)
- The effect of subject age on RT might be different for one item than another: e.g., modern words might be recognized faster by younger participants
  = Random Slope for Subject Age per Item (i.e. \(\beta_{\textrm{SA}}\) varies per item)
Note that it is essential to test for random slopes!

Question 1

Random slopes are necessary!

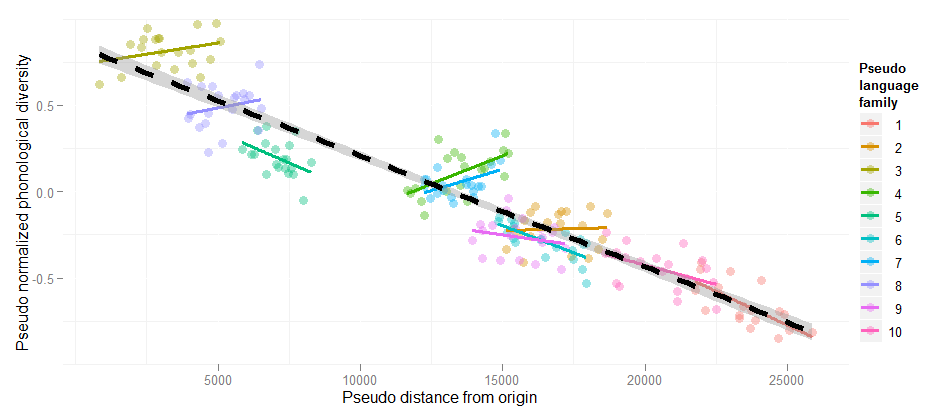
                                    Estimate  Std. Error  t value  Pr(>|t|)    
Linear regression     DistOrigin  -6.418e-05   1.808e-06   -35.49    <2e-16
+ Random intercepts   DistOrigin  -2.224e-05   6.863e-06   -3.240    <0.001
+ Random slopes       DistOrigin  -1.478e-05   1.519e-05   -0.973    n.s.

(This example is explained at the HLP/Jaeger lab blog)

Modeling the variance structure

Mixed-effects regression allow us to use random intercepts and slopes (i.e. adjustments to the population intercept and slopes) to include the variance structure in our data
- Parsimony: a single parameter (standard deviation) models this variation for every random slope or intercept (a normal distribution with mean 0 is assumed)
- The slope and intercept adjustments are Best Linear Unbiased Predictors
- Model comparison determines the inclusion of random intercepts and slopes
Mixed-effects regression is only required when each level of the random-effect factor has multiple observations (e.g., participants respond to multiple items)

Specific models for every observation

RT = 200 - 5WF + 3WL + 10SA (general model)
- The intercepts and slopes may vary (according to the estimated variation for each parameter) and this influences the word- and subject-specific values
RT = 400 - 5WF + 3WL - 2SA (word: scythe)
RT = 300 - 5WF + 3WL + 15SA (word: twitter)
RT = 300 - 7WF + 3WL + 10SA (subject: non-native)
RT = 150 - 5WF + 3WL + 10SA (subject: fast)
And it is not hard to use!
- lmer( RT ~ WF + WL + SA + (1+SA|Wrd) + (1+WF|Subj) )
- (lmer automatically discovers random-effects structure: nested/crossed)

Variability in intercept and slope

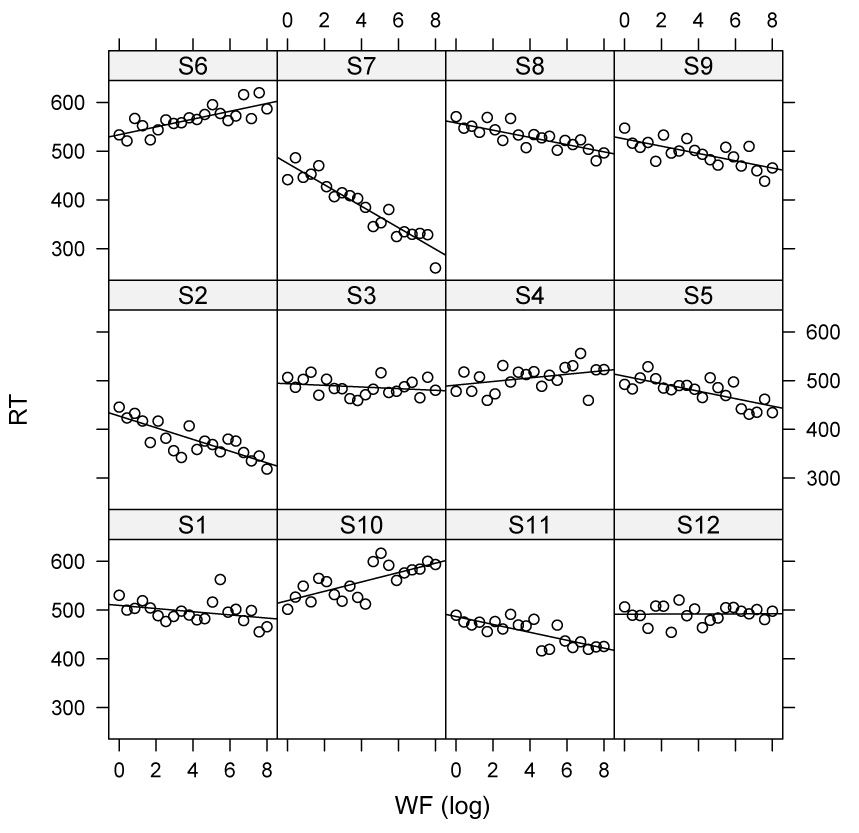
Random slopes and intercepts may be (cor)related

For example:

Subject	Intercept	WF slope
S1	525	-2
S2	400	-1
S3	500	-2
S4	550	-3
S5	450	-2
S6	600	-4
S7	300	0

BLUPs of `lmer` do not suffer from shrinkage

The BLUPS (i.e. adjustment to the model estimates per item/participant) are close to the real adjustments, as lmer takes into account regression towards the mean (fast subjects will be slower next time, and slow subjects will be faster) thereby avoiding overfitting and improving prediction - see Efron & Morris (1977)

Question 2

Center your variables (i.e. subtract the mean)!

Otherwise random slopes and intercepts may show a spurious correlation
Also helps the interpretation of interactions (see this lecture)

Mixed-effects regression assumptions

Independent observations within each level of the random-effect factor
Relation between dependent and independent variables linear
No strong multicollinearity
Residuals are not autocorrelated
Homoscedasticity of variance in residuals
Residuals are normally distributed
(Similar assumptions as for regression)

Question 3

Model criticism

Check the distribution of residuals
- If not normally distributed and/or heteroscedastic residuals then transform dependent variable or use generalized linear mixed-effects regression modeling
Check outlier characteristics and refit the model when large outliers are excluded to verify that your effects are not ‘carried’ by these outliers
- See regression lecture

Model selection I

“The data analyst knows more than the computer.” (Henderson & Velleman, 1981)
- Get to know your data!
There is no adequate automatic procedure to find the best model
Fitting the most complex random effects structure (Barr et al., 2013) is mostly not a good idea
- The model may not converge, or is uninterpretable (see Baayen et al., 2017)
- The power of your method is reduced (Matuschek et al., 2017)

Model selection II

My stepwise variable-selection procedure (for exploratory analysis):
- Include random intercepts
- Add other potential explanatory variables one-by-one
- Insignificant predictors are dropped
- Test predictors for inclusion which were excluded at an earlier stage
- Test possible interactions (don’t make it too complex)
- Try to break the model by including significant predictors as random slopes
- Only choose a more complex model if supported by model comparison

Model selection III

For a hypothesis-driven analysis, stepwise selection is problematic
- Confidence intervals too narrow: \(p\)-values too low (multiple comparisons)
- See, e.g., Burnham & Anderson (1998)
Solutions:
- Careful specification of potential a priori models lining up with the hypotheses (including optimal random-effects structure) and evaluating only these models
  - This may be followed by an exploratory procedure
- Validating a stepwise procedure via cross validation (e.g., bootstrap analysis)

Case study: influence of alcohol on L1 and L2

Reported in Wieling et al. (2019) and Offrede et al. (2020)
Assess influence of alcohol (BAC) on L1 (clarity) vs. L2 (nativelikeness) ratings
Prediction: higher BAC has negative effect on L1, but positive effect on L2 nativelikeness (based on Renner et al., 2018)
~80 recordings from native Dutch speakers included (all BACs < 0.8, no drugs)
Dutch ratings were given by >100 native (sober) Dutch speakers (at Lowlands)
English ratings were given by >100 native American English speakers (online)
Dependent variable is \(z\)-transformed rating (5-point Likert scale)
Numerical variables are centered (not \(z\)-transformed)

Dataset

load('lls.rda')
head(lls)

          SID   BAC Sex BirthYear L2cnt SelfEN LivedEN L2anxiety   Edu      LID Lang Rating
1 S0045188-17 0.392   F     -5.66 -1.04  0.463       Y     0.357 0.817 L0637009   NL  0.946
2 S0045188-17 0.392   F     -5.66 -1.04  0.463       Y     0.357 0.817     L196   EN  0.330
3 S0045188-17 0.392   F     -5.66 -1.04  0.463       Y     0.357 0.817      L86   EN -0.298
4 S0045188-17 0.392   F     -5.66 -1.04  0.463       Y     0.357 0.817 L0614758   NL  0.325
5 S0045188-17 0.392   F     -5.66 -1.04  0.463       Y     0.357 0.817     L220   EN -0.435
6 S0045188-17 0.392   F     -5.66 -1.04  0.463       Y     0.357 0.817     L225   EN -0.239

Fitting our first model

(fitted in R version 4.5.0 (2025-04-11 ucrt), `lme4` version 1.1.37)

library(lme4)
m <- lmer(Rating ~ BAC + (1|SID) + (1|LID), data=lls) # does not converge

boundary (singular) fit: see help('isSingular')

summary(m)$coef # show fixed effects

            Estimate Std. Error t value
(Intercept)    0.144     0.0638   2.252
BAC           -0.221     0.3262  -0.677

summary(m)$varcor # show random-effects part only: no variability per listener (due to z-scaling)

 Groups   Name        Std.Dev.
 LID      (Intercept) 0.000   
 SID      (Intercept) 0.560   
 Residual             0.738

Evaluating our hypothesis (1)

(note: random intercept for LID excluded)

m1 <- lmer(Rating ~ Lang * BAC + (1|SID), data=lls)

This model represents our hypothesis test (but likely without the correct random-effects structure)

Results (likely overestimating significance)

summary(m1, cor=F) # suppress estimated correlation of regression coefficient; Note: |t| > 2 => p < .05 (N > 100)

Linear mixed model fit by REML ['lmerMod']
Formula: Rating ~ Lang * BAC + (1 | SID)
   Data: lls

REML criterion at convergence: 5853

Scaled residuals: 
   Min     1Q Median     3Q    Max 
-3.668 -0.647  0.032  0.707  3.187 

Random effects:
 Groups   Name        Variance Std.Dev.
 SID      (Intercept) 0.305    0.552   
 Residual             0.533    0.730   
Number of obs: 2541, groups:  SID, 82

Fixed effects:
            Estimate Std. Error t value
(Intercept)   0.0883     0.0635    1.39
LangNL        0.2430     0.0358    6.78
BAC          -0.0592     0.3255   -0.18
LangNL:BAC   -0.7286     0.1938   -3.76

Visualization helps interpretation

library(visreg)
visreg(m1,'BAC', by='Lang',overlay=T, xlab='BAC (centered)', ylab='Rating')

Interpretation: a higher BAC has a negative effect on L1, but not L2

Is the added interaction an improvement?

m0 <- lmer(Rating ~ Lang + (1|SID), data=lls) # comparison: best simpler model (BAC n.s.)
anova(m0, m1) # interaction necessary

Data: lls
Models:
m0: Rating ~ Lang + (1 | SID)
m1: Rating ~ Lang * BAC + (1 | SID)
   npar  AIC  BIC logLik -2*log(L) Chisq Df Pr(>Chisq)    
m0    4 5866 5889  -2929      5858                        
m1    6 5855 5890  -2921      5843  14.7  2    0.00063 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Evaluating our hypothesis (2): adding a random slope

m2 <- lmer(Rating ~ Lang * BAC + (1 + Lang|SID), data=lls)
anova(m1, m2, refit=FALSE) # random slope necessary? (REML model comparison)

Data: lls
Models:
m1: Rating ~ Lang * BAC + (1 | SID)
m2: Rating ~ Lang * BAC + (1 + Lang | SID)
   npar  AIC  BIC logLik -2*log(L) Chisq Df Pr(>Chisq)    
m1    6 5865 5900  -2927      5853                        
m2    8 5626 5672  -2805      5610   244  2     <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

This model represents the appropriate hypothesis test as it includes the adequate random-effects structure

Intermezzo: ML or REML model comparison?

Restricted Maximum Likelihood (REML; default lmer fitting method) is appropriate when comparing 2 models differing exclusively in the random-effects structure
- The REML score depends on which fixed effects are in the model, so REML values are not comparable if the fixed effects change
- As REML is considered to give better estimates for the random effects, it is recommended to fit your final model (for reporting and inference) using REML
ML is appropriate when comparing models differing only in the fixed effects
- anova automatically refits the models with ML, unless refit=F is specified
Never compare 2 models differing in both fixed and random effects
Only compare models which differ minimally (e.g., only in 1 random slope)

Results of hypothesis test

summary(m2, cor=F)$coef # show only fixed effects of model with random slope

            Estimate Std. Error t value
(Intercept)   0.0988     0.0747   1.322
LangNL        0.2544     0.0815   3.121
BAC           0.0994     0.3925   0.253
LangNL:BAC   -0.9875     0.4265  -2.316

Note the higher |\(t\)|-values in the model without the random slope:

summary(m1, cor=F)$coef # results of model without random slope

            Estimate Std. Error t value
(Intercept)   0.0883     0.0635   1.391
LangNL        0.2430     0.0358   6.785
BAC          -0.0592     0.3255  -0.182
LangNL:BAC   -0.7286     0.1938  -3.759

Random effects: correlation parameter

summary(m2, cor=F)$varcor # show only random effects of model with random slope

 Groups   Name        Std.Dev. Corr 
 SID      (Intercept) 0.653         
          LangNL      0.653    -0.83
 Residual             0.683

Note the absence of the random slope in the random-intercept-only model:

summary(m1, cor=F)$varcor # results of model without random slope

 Groups   Name        Std.Dev.
 SID      (Intercept) 0.552   
 Residual             0.730

A note about random-effect correlation parameters

In the previous model a correlation is assumed between random intercept and slope: (1+X|RF)
- Any terms before the | are assumed to be correlated and a correlation parameter is calculated for each pair
To exclude the correlation parameter, a simpler model can be specified as follows: (1|RF) + (0+X|RF) (alternatively: (1+X||RF))
- Model comparison (with refit=FALSE) is used to determine the best model when only random effects differ
Factorial predictors (such as Lang) should always be grouped with the intercept: (1+Lang|SID), but not: (1|SID) + (0 + Lang|SID)

Interpretation of correlation parameter

plot( coef(m2)$SID[,"(Intercept)"],  coef(m2)$SID[,"LangNL"], xlab='By-subject random intercept', 
      ylab='By-subject random slope for language contrast')

Interpretation: speakers with higher ratings for English (intercept), have lower ratings for Dutch and vice versa (however: categorical variables are not centered)

Visualizing the results of the hypothesis test

visreg(m2,'BAC',by='Lang',overlay=T, xlab='BAC (centered)', ylab='Rating')

Interpretation as before: a higher BAC has a negative effect on L1, but not on L2

Alternative summary

m2b <- lmer(Rating ~ Lang : BAC + Lang + (1 + Lang|SID), data=lls) # instead of Lang * BAC
summary(m2b)$coef # effect of BAC per language separately

            Estimate Std. Error t value
(Intercept)   0.0988     0.0747   1.322
LangNL        0.2544     0.0815   3.121
LangEN:BAC    0.0994     0.3925   0.253
LangNL:BAC   -0.8882     0.2684  -3.309

summary(m2)$coef # original model: effect of BAC for NL vs EN

            Estimate Std. Error t value
(Intercept)   0.0988     0.0747   1.322
LangNL        0.2544     0.0815   3.121
BAC           0.0994     0.3925   0.253
LangNL:BAC   -0.9875     0.4265  -2.316

Exploratory analysis

Hypothesis seems partially supported
But this may be caused by other variables:
- L2 anxiety
- L2 self rating
- (Other control variables)
It may also be caused by the presence of atypical outliers
Next step: exploratory analysis

Effect of speaker’s sex?

m3 <- lmer(Rating ~ Lang * BAC + Sex + (1 + Lang|SID), data=lls)
summary(m3)$coef

            Estimate Std. Error t value
(Intercept)   0.1347     0.0870   1.549
LangNL        0.2532     0.0815   3.107
BAC           0.1325     0.3987   0.332
SexM         -0.0815     0.0973  -0.838
LangNL:BAC   -0.9801     0.4265  -2.298

anova(m2,m3)$P[2] # p-value from anova: Sex not necessary (nor in interaction; not shown)

[1] 0.404

Effect of speaker’s year of birth?

m3 <- lmer(Rating ~ Lang * BAC + BirthYear + (1 + Lang|SID), data=lls)
summary(m3)$coef

            Estimate Std. Error t value
(Intercept)  0.09969    0.07472   1.334
LangNL       0.25462    0.08171   3.116
BAC          0.08313    0.39269   0.212
BirthYear    0.00603    0.00495   1.217
LangNL:BAC  -0.99645    0.42764  -2.330

anova(m2,m3)$P[2] # BirthYear not necessary (nor in interaction with language; not shown)

[1] 0.217

Effect of speaker’s education?

m3 <- lmer(Rating ~ Lang * BAC + Edu + (1 + Lang|SID), data=lls)
summary(m3)$coef

            Estimate Std. Error t value
(Intercept)    0.102     0.0709   1.443
LangNL         0.255     0.0817   3.115
BAC            0.200     0.3734   0.536
Edu            0.112     0.0341   3.288
LangNL:BAC    -1.034     0.4266  -2.424

anova(m2,m3)$P[2] # Education necessary (but not in interaction with language; not shown)

[1] 0.00139

Effect of living in an English-speaking country?

m4 <- lmer(Rating ~ Lang * BAC + Edu + LivedEN + (1 + Lang|SID), data=lls)
summary(m4)$coef

            Estimate Std. Error t value
(Intercept)   0.0831     0.0732   1.134
LangNL        0.2526     0.0817   3.091
BAC           0.2027     0.3708   0.546
Edu           0.1126     0.0342   3.290
LivedENY      0.1116     0.1147   0.973
LangNL:BAC   -1.0368     0.4264  -2.432

anova(m3,m4)$P[2] # LivedEN not necessary (also not in interaction with language; not shown)

[1] 0.327

Effect of self-rated English proficiency?

m4 <- lmer(Rating ~ Lang * BAC + Edu + SelfEN + (1 + Lang|SID), data=lls)
summary(m4)$coef

            Estimate Std. Error t value
(Intercept)   0.1077     0.0644   1.671
LangNL        0.2491     0.0824   3.021
BAC           0.1675     0.3401   0.493
Edu           0.0758     0.0343   2.211
SelfEN        0.1299     0.0370   3.507
LangNL:BAC   -1.0967     0.4283  -2.561

anova(m3,m4)$P[2] # SelfEN necessary

[1] 0.00135

Self-rated English proficiency: interaction?

m5 <- lmer(Rating ~ Lang * BAC + Edu + SelfEN * Lang + (1 + Lang|SID), data=lls)
summary(m5)$coef

              Estimate Std. Error t value
(Intercept)     0.1087     0.0612   1.775
LangNL          0.2474     0.0753   3.285
BAC             0.0665     0.3236   0.206
Edu             0.0741     0.0344   2.157
SelfEN          0.2874     0.0541   5.309
LangNL:BAC     -0.9385     0.3933  -2.386
LangNL:SelfEN  -0.2519     0.0630  -3.996

anova(m4,m5)$P[2] # interaction necessary

[1] 0.000103

Visual interpretation of interaction

visreg(m5,'SelfEN',by='Lang',overlay=T, xlab='EN self rating (centered)', ylab='Rating')

Interpretation: a higher self-rated English proficiency is only predictive for the English ratings, not the Dutch ratings (unsurprisingly)

Effect of L2 count?

m6 <- lmer(Rating ~ Lang * BAC + Edu + SelfEN * Lang + L2cnt + (1 + Lang|SID), data=lls)
summary(m6)$coef

              Estimate Std. Error t value
(Intercept)     0.1080     0.0599   1.802
LangNL          0.2500     0.0755   3.314
BAC             0.1092     0.3172   0.344
Edu             0.0635     0.0339   1.875
SelfEN          0.2787     0.0531   5.246
L2cnt           0.1012     0.0467   2.168
LangNL:BAC     -0.9356     0.3937  -2.377
LangNL:SelfEN  -0.2499     0.0632  -3.956

anova(m5,m6)$P[2] # L2cnt necessary

[1] 0.028

Note that the variable Edu now does not have an absolute \(t\)-value > 2 anymore, but we retain it as it is close to significance (\(p \approx 0.06\) based on anova)

For both English and Dutch, or only English?

m7 <- lmer(Rating ~ Lang * BAC + Edu + SelfEN * Lang + L2cnt * Lang + (1 + Lang|SID), data=lls)
summary(m7)$coef

              Estimate Std. Error t value
(Intercept)     0.1076     0.0601   1.792
LangNL          0.2501     0.0758   3.300
BAC             0.1237     0.3183   0.389
Edu             0.0630     0.0338   1.863
SelfEN          0.2746     0.0536   5.127
L2cnt           0.1340     0.0677   1.979
LangNL:BAC     -0.9640     0.3972  -2.427
LangNL:SelfEN  -0.2432     0.0642  -3.785
LangNL:L2cnt   -0.0576     0.0861  -0.668

anova(m6,m7)$P[2] # no interaction necessary: L2cnt affects both languages similarly

[1] 0.49

Effect of L2 anxiety?

m7 <- lmer(Rating ~ Lang * BAC + Edu + SelfEN * Lang + L2cnt + L2anxiety + (1 + Lang|SID), data=lls)
summary(m7)$coef

              Estimate Std. Error t value
(Intercept)     0.1098     0.0580   1.892
LangNL          0.2453     0.0755   3.251
BAC             0.1042     0.3072   0.339
Edu             0.0606     0.0327   1.854
SelfEN          0.2026     0.0599   3.384
L2cnt           0.1202     0.0456   2.638
L2anxiety      -0.2277     0.0918  -2.481
LangNL:BAC     -0.9463     0.3931  -2.407
LangNL:SelfEN  -0.2526     0.0632  -3.998

anova(m6,m7)$P[2] # L2anxiety necessary

[1] 0.0118

For both English and Dutch, or only English?

m8 <- lmer(Rating ~ Lang * BAC + Edu + SelfEN * Lang + L2cnt + L2anxiety * Lang  + (1 + Lang|SID), data=lls)
summary(m8)$coef

                 Estimate Std. Error t value
(Intercept)        0.1103     0.0581   1.900
LangNL             0.2462     0.0756   3.259
BAC                0.0949     0.3075   0.309
Edu                0.0607     0.0327   1.857
SelfEN             0.1721     0.0680   2.531
L2cnt              0.1206     0.0456   2.644
L2anxiety         -0.3202     0.1340  -2.389
LangNL:BAC        -0.9293     0.3940  -2.359
LangNL:SelfEN     -0.1973     0.0861  -2.292
LangNL:L2anxiety   0.1653     0.1747   0.946

anova(m7,m8)$P[2] # no interaction necessary: L2anxiety affects both languages similarly

[1] 0.337

Best model?

Since SID is the only random-effect factor, and the characteristics are unique per SID, there are no additional random slopes to test
All fixed-effects were tested (not all n.s. interactions were shown)
Conclusion: m7 is the best model!

Testing assumptions: multicollinearity

library(car)
vif(m7) # Should be lower < 5 (for centered numerical variables): OK

       Lang         BAC         Edu      SelfEN       L2cnt   L2anxiety    Lang:BAC 
       1.00        2.32        1.19        3.40        1.08        1.94        2.30 
Lang:SelfEN 
       2.34

Testing assumptions: autocorrelation

acf(resid(m7)) # no autocorrelation

Testing assumptions: normality

qqnorm(resid(m7)) # OK
qqline(resid(m7))

Testing assumptions: heteroscedasticity

plot(fitted(m7),resid(m7)) # some heteroscedasticity

Model criticism: countering outlier influence

lls2 <- lls[ abs(scale(resid(m7))) < 2.5 , ] # trimmed model: 98.5% of original data 
m7.2 <- lmer(Rating ~ Lang * BAC + Edu + SelfEN * Lang + L2cnt + L2anxiety + (1 + Lang|SID), data = lls2)
summary(m7.2)$coef

              Estimate Std. Error t value
(Intercept)     0.1161     0.0594   1.955
LangNL          0.2493     0.0758   3.289
BAC             0.1342     0.3145   0.427
Edu             0.0627     0.0332   1.887
SelfEN          0.2055     0.0612   3.360
L2cnt           0.1245     0.0463   2.687
L2anxiety      -0.2451     0.0933  -2.626
LangNL:BAC     -0.9850     0.3948  -2.495
LangNL:SelfEN  -0.2708     0.0636  -4.260

The BAC interaction with language remains the same: significantly more negative effect of BAC on ratings for Dutch compared to English

Question 4

Checking the residuals of the trimmed model

par(mfrow=c(1,2))
qqnorm(resid(m7.2)) # reasonably OK
qqline(resid(m7.2))
plot(fitted(m7.2),resid(m7.2)) # better

Bootstrap sampling shows similar results

library(boot)
(bsm7.2 <- confint(m7.2, method="boot", nsim = 1000, level = 0.95))

                 2.5 %  97.5 %
.sig01         0.42482  0.6031
.sig02        -0.88736 -0.6747
.sig03         0.49042  0.7369
.sigma         0.62306  0.6593
(Intercept)    0.00145  0.2273
LangNL         0.10500  0.4073
BAC           -0.48284  0.7246
Edu            0.00206  0.1296
SelfEN         0.07526  0.3238
L2cnt          0.03867  0.2142
L2anxiety     -0.43556 -0.0652
LangNL:BAC    -1.73253 -0.2097
LangNL:SelfEN -0.40298 -0.1429

Note that the 95% CI of the variable Edu does not contain 0 and therefore indicates it is a significant predictor

Recap

We have learned:
- How to interpret mixed-effects regression results
- How to use lmer to conduct mixed-effects regression
- How to include random intercepts and random slopes in lmer and why these are essential when you have multiple responses per subject or item
Associated lab session:
- https://www.let.rug.nl/wieling/Statistics/Mixed-Effects/lab
  - Lab session contains additional information: how to do multiple comparisons, and using other optimizers (countering convergence problems)

Evaluation

Questions?

Thank you for your attention!

https://www.martijnwieling.nl

m.b.wieling@rug.nl

Mixed-effects regression

This lecture

Introduction

The language-as-fixed-effect fallacy

Why linguists are not always good statisticians

Our problems solved…

Recap: multiple regression (1)

Recap: multiple regression (2)

Mixed-effects regression modeling: introduction

What are random-effects factors?

Question 1

Random slopes are necessary!

Modeling the variance structure

Specific models for every observation

Variability in intercept and slope

Random slopes and intercepts may be (cor)related

BLUPs of lmer do not suffer from shrinkage

Question 2

Center your variables (i.e. subtract the mean)!

Mixed-effects regression assumptions

Question 3

Model criticism

Model selection I

Model selection II

Model selection III

Case study: influence of alcohol on L1 and L2

Case study: influence of alcohol on L1 and L2

Dataset

Fitting our first model

(fitted in R version 4.5.0 (2025-04-11 ucrt), lme4 version 1.1.37)

Evaluating our hypothesis (1)

(note: random intercept for LID excluded)

Results (likely overestimating significance)

Visualization helps interpretation

Is the added interaction an improvement?

Evaluating our hypothesis (2): adding a random slope

Intermezzo: ML or REML model comparison?

Results of hypothesis test

Random effects: correlation parameter

A note about random-effect correlation parameters

Interpretation of correlation parameter

Visualizing the results of the hypothesis test

Alternative summary

Exploratory analysis

Effect of speaker’s sex?

Effect of speaker’s year of birth?

Effect of speaker’s education?

Effect of living in an English-speaking country?

Effect of self-rated English proficiency?

Self-rated English proficiency: interaction?

Visual interpretation of interaction

Effect of L2 count?

For both English and Dutch, or only English?

Effect of L2 anxiety?

For both English and Dutch, or only English?

Best model?

Testing assumptions: multicollinearity

Testing assumptions: autocorrelation

Testing assumptions: normality

Testing assumptions: heteroscedasticity

Model criticism: countering outlier influence

Question 4

Checking the residuals of the trimmed model

Bootstrap sampling shows similar results

Recap

Evaluation

Questions?

BLUPs of `lmer` do not suffer from shrinkage

(fitted in R version 4.5.0 (2025-04-11 ucrt), `lme4` version 1.1.37)