Statistiek I

Multiple regression and Cronbach’s alpha

Martijn Wieling

Question 1: last lecture

Last lecture

Simple linear regression with a nominal variable
Multiple linear regression with multiple independent variables
Introduction to multiple linear regression with an interaction

This lecture

Part I: Multiple regression with an interaction (continued)
Part II: Cronbach’s alpha to assess the reliability of questionnaires
Part III: Recap of all lectures (time permitting)

Part I: Dataset for multiple regression

English L2 phonetically transcribed pronunciation data from Speech Accent Archive
Goal: identify potential determinants of L2 speakers’ English pronunciation quality
Nativelikeness measured by comparing pronunciations to American English speakers
Here: data from 325 L2 non-Indo-European speakers of English
We assess the effect of age and length of residence in an English-speaking country
- Age: first as nominal variable (young vs. old), later as numerical variable
Note that we don’t specify hypotheses here, as we conduct an exploratory analysis
- We aim to identify potentially “interesting” variables, which may serve to inform future hypotheses and data collection efforts
For simplicity, we (wrongly) ignore variability linked to native language and country
- Mixed-effects regression is required for this: covered in Statistiek II

Investigating the influence of length of residence

m <- lm(NL ~ LR, data=saa) # LR: length of residence (longer = more nativelike)
summary(m)


Call:
lm(formula = NL ~ LR, data = saa)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.9902 -0.6875  0.0454  0.6867  2.2630 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.15505    0.06455   -2.40    0.017 *  
LR           0.02041    0.00466    4.38  1.6e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.973 on 323 degrees of freedom
Multiple R-squared:  0.0561,    Adjusted R-squared:  0.0531 
F-statistic: 19.2 on 1 and 323 DF,  p-value: 1.61e-05

Question 2

Adding a second variable in a multiple regression model

m2 <- lm(NL ~ LR + AgeGroup, data=saa) 
summary(m2)


Call:
lm(formula = NL ~ LR + AgeGroup, data = saa)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.0168 -0.6580  0.0846  0.6557  2.2357 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.12920    0.06498   -1.99    0.048 *  
LR           0.02770    0.00554    5.00  9.3e-07 ***
AgeGroupOld -0.37194    0.15523   -2.40    0.017 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.966 on 322 degrees of freedom
Multiple R-squared:  0.0726,    Adjusted R-squared:  0.0668 
F-statistic: 12.6 on 2 and 322 DF,  p-value: 5.38e-06

Model comparison: additional predictor necessary?

anova(m, m2)

Analysis of Variance Table

Model 1: NL ~ LR
Model 2: NL ~ LR + AgeGroup
  Res.Df RSS Df Sum of Sq    F Pr(>F)  
1    323 306                           
2    322 300  1      5.36 5.74  0.017 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The additional model complexity is supported by the improved fit to the data

Which variable is most important?

saa$LR.z <- (saa$LR - mean(saa$LR)) / sd(saa$LR)
summary(m2 <- lm(NL ~ LR.z + AgeGroup, data=saa)) # LR has larger effect (0.32 per SD; AG: 0.37 in total)


Call:
lm(formula = NL ~ LR.z + AgeGroup, data = saa)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.0168 -0.6580  0.0846  0.6557  2.2357 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.0813     0.0634    1.28    0.201    
LR.z          0.3214     0.0642    5.00  9.3e-07 ***
AgeGroupOld  -0.3719     0.1552   -2.40    0.017 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.966 on 322 degrees of freedom
Multiple R-squared:  0.0726,    Adjusted R-squared:  0.0668 
F-statistic: 12.6 on 2 and 322 DF,  p-value: 5.38e-06

Interpretation of intercept in the regression model

summary(m2)$coef # only show coefficients

            Estimate Std. Error t value Pr(>|t|)
(Intercept)    0.081      0.063     1.3  2.0e-01
LR.z           0.321      0.064     5.0  9.3e-07
AgeGroupOld   -0.372      0.155    -2.4  1.7e-02

Young people (AgeGroup == 'Young') with an avg. length of residence (LR.z == 0) have a predicted nativelikeness of 0.081

Interpreting the regression model logically

summary(m2)$coef # only show coefficients

            Estimate Std. Error t value Pr(>|t|)
(Intercept)    0.081      0.063     1.3  2.0e-01
LR.z           0.321      0.064     5.0  9.3e-07
AgeGroupOld   -0.372      0.155    -2.4  1.7e-02

Summary shows \(\beta_\textrm{LR.z}\) = 0.32
- For every increase of LR of 1 SD, the nativelikeness score increases by 0.32
Summary shows \(\beta_\textrm{AgeGroupOld}\) = -0.37
- Older speakers have a nativelikeness score that is 0.37 lower than younger speakers
Fitted (predicted) value of the model can be determined using regression formula
- \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 \implies\) NL = 0.08 + 0.32 * LR.z + -0.37 * AgeGroupOld
- AgeGroupOld equals 1 for the Old group and 0 for the Young group

Interpreting the regression model numerically

summary(m2)$coef

            Estimate Std. Error t value Pr(>|t|)
(Intercept)    0.081      0.063     1.3  2.0e-01
LR.z           0.321      0.064     5.0  9.3e-07
AgeGroupOld   -0.372      0.155    -2.4  1.7e-02

\(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 \implies\) NL = 0.08 + 0.32 * LR.z + -0.37 * AgeGroupOld
For LR.z of 0 and AgeGroup Young: 0.08 + 0.32 \(\times\) 0 + -0.37 \(\times\) 0 = 0.08 (= Intercept)
For LR.z of 0.5 and AgeGroup Old: 0.08 + 0.32 \(\times\) 0.5 + -0.37 \(\times\) 1 = -0.13
Note that the effects are independent and do not influence each other!

Question 3

Interpreting the regression model visually

library(visreg)
par(mfrow=c(1,3))
visreg(m2,'LR.z')
visreg(m2,'AgeGroup')
visreg(m2, 'LR.z', by='AgeGroup', overlay=TRUE) # shows independence of effects

Interaction between nominal and numerical variable

summary(m3 <- lm(NL ~ LR.z * AgeGroup, data=saa)) # LR * AG == LR + AG + LR:AG (== AG * LR)


Call:
lm(formula = NL ~ LR.z * AgeGroup, data = saa)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.9464 -0.6658  0.0731  0.6751  2.3044 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)        0.1386     0.0684    2.03    0.044 *  
LR.z               0.5190     0.1114    4.66  4.7e-06 ***
AgeGroupOld       -0.3289     0.1556   -2.11    0.035 *  
LR.z:AgeGroupOld  -0.2943     0.1360   -2.16    0.031 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.961 on 321 degrees of freedom
Multiple R-squared:  0.0859,    Adjusted R-squared:  0.0774 
F-statistic: 10.1 on 3 and 321 DF,  p-value: 2.37e-06

Interaction necessary to include?

anova(m2, m3)

Analysis of Variance Table

Model 1: NL ~ LR.z + AgeGroup
Model 2: NL ~ LR.z * AgeGroup
  Res.Df RSS Df Sum of Sq    F Pr(>F)  
1    322 300                           
2    321 296  1      4.32 4.68  0.031 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Recall regression formula for interaction from last lecture

Regression formula \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_{1,2} x_1 x_2 + \epsilon\)
- \(y\): dependent variable (= predicted or fitted values), \(x_i\): independent variables, \(\epsilon\): resid.
  - \(\beta_0\): intercept (value of \(y\) when all \(x_i's\) are \(0\))
  - \(\beta_1\): influence (slope) of \(x_1\) on \(y\) when \(x_2\) equals 0
  - \(\beta_2\): influence (slope) of \(x_2\) on \(y\) when \(x_1\) equals 0
  - \(\beta_{1,2}\): interaction effect (slope) of \(x_1\) and \(x_2\)

Interpreting the interaction numerically

summary(m3)$coef

                 Estimate Std. Error t value Pr(>|t|)
(Intercept)          0.14      0.068     2.0  4.4e-02
LR.z                 0.52      0.111     4.7  4.7e-06
AgeGroupOld         -0.33      0.156    -2.1  3.5e-02
LR.z:AgeGroupOld    -0.29      0.136    -2.2  3.1e-02

Regression formula \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_{1,2} x_1 x_2 \implies\)
NL = 0.14 + 0.52 * LR.z + -0.33 * AGOld + -0.29 * LR.z * AGOld
- For LR.z of 0 and AgeGroup Young: 0.14 + 0.52\(\times\)0 + -0.33\(\times\)0 + -0.29\(\times\)0\(\times\)0 = 0.14
- For LR.z of 0 and AgeGroup Old: 0.14 + 0.52\(\times\)0 + -0.33\(\times\)1 + -0.29\(\times\)0\(\times\)1 = -0.19
- For LR.z of 0.5 and AgeGroup Old: 0.14 + 0.52\(\times\)0.5 + -0.33\(\times\)1 +-0.29\(\times\)0.5\(\times\)1 = -0.075

Question 4

Interpreting the interaction logically

summary(m3)$coef

                 Estimate Std. Error t value Pr(>|t|)
(Intercept)          0.14      0.068     2.0  4.4e-02
LR.z                 0.52      0.111     4.7  4.7e-06
AgeGroupOld         -0.33      0.156    -2.1  3.5e-02
LR.z:AgeGroupOld    -0.29      0.136    -2.2  3.1e-02

For the Young AgeGroup, each unit increase of LR increases NL by 0.52
For the Old AgeGroup, each unit increase of LR increases NL by 0.52 + -0.29 = 0.23
The LR slope is shifted downwards by 0.23 for the Old Agegroup
Summary: the effect of LR is less beneficial for older people
- Learning a language through immersion is more effective when young than old

Interpreting the interaction visually

                 Estimate Std. Error t value Pr(>|t|)
(Intercept)          0.14      0.068     2.0  4.4e-02
LR.z                 0.52      0.111     4.7  4.7e-06
AgeGroupOld         -0.33      0.156    -2.1  3.5e-02
LR.z:AgeGroupOld    -0.29      0.136    -2.2  3.1e-02

visreg(m3, "LR.z", by="AgeGroup")

Interaction between two nominal variables

m4 <- lm(NL ~ AgeGroup * Sex, data=saa) # We drop LR for simplicity (normally you would include it)
summary(m4) # no significant predictors


Call:
lm(formula = NL ~ AgeGroup * Sex, data = saa)

Residuals:
   Min     1Q Median     3Q    Max 
-3.147 -0.648  0.042  0.696  2.142 

Coefficients:
                    Estimate Std. Error t value Pr(>|t|)
(Intercept)          -0.0303     0.0930   -0.33     0.74
AgeGroupOld           0.2448     0.2052    1.19     0.23
SexMale               0.0337     0.1262    0.27     0.79
AgeGroupOld:SexMale  -0.3308     0.2718   -1.22     0.22

Residual standard error: 1 on 321 degrees of freedom
Multiple R-squared:  0.00546,   Adjusted R-squared:  -0.00384 
F-statistic: 0.587 on 3 and 321 DF,  p-value: 0.624

Is this model an improvement over the simpler model?

Question 5

Which model for comparison?

summary(m0d <- lm(NL ~ AgeGroup + Sex, data=saa))$coef # AgeGroup and Sex: both not significant

            Estimate Std. Error t value Pr(>|t|)
(Intercept)  0.00844     0.0875  0.0965    0.923
AgeGroupOld  0.05616     0.1347  0.4171    0.677
SexMale     -0.03760     0.1119 -0.3362    0.737

summary(m0b <- lm(NL ~ AgeGroup, data=saa))$coef # only AgeGroup: not significant

            Estimate Std. Error t value Pr(>|t|)
(Intercept)  -0.0120     0.0628  -0.191    0.849
AgeGroupOld   0.0549     0.1344   0.408    0.683

summary(m0c <- lm(NL ~ Sex, data=saa))$coef # only Sex: not significant

            Estimate Std. Error t value Pr(>|t|)
(Intercept)   0.0200     0.0829   0.241    0.810
SexMale      -0.0363     0.1117  -0.325    0.745

None of the simpler models have a significant predictor, so which one to use?

Note about model comparison for an interaction

Note that a model with an interaction term (A:B) should be compared to the best model without that term
- This is the model including A + B, if both terms are significant
- This is the model only including A, if A is significant and B is not
- This is the model only including B, if B is significant and A is not
- This is the model without A and B, if neither are significant
It is important to get this comparison right, as an interaction might provide an improvement over including A + B (if both are not significant), but may not be an improvement over the model without A and B.
- In that case one should stick with the model without A, B, or their interaction

Model comparison

m0a <- lm(NL ~ 1, data=saa) # model without AgeGroup and Sex for comparison
anova(m0a, m4) # interaction is not supported

Analysis of Variance Table

Model 1: NL ~ 1
Model 2: NL ~ AgeGroup * Sex
  Res.Df RSS Df Sum of Sq    F Pr(>F)
1    324 324                         
2    321 322  3      1.77 0.59   0.62

In line with our guess, the interaction between AgeGroup and Sex is not supported
AgeGroup is only significant if we also take into account the effect of LR
- As mentioned: in a multiple regression model the interpretation of the effect of a variable always entails that one controls for all other variables in the model

Visualization (of non-significant interaction)

                    Estimate Std. Error t value Pr(>|t|)
(Intercept)           -0.030      0.093   -0.33     0.74
AgeGroupOld            0.245      0.205    1.19     0.23
SexMale                0.034      0.126    0.27     0.79
AgeGroupOld:SexMale   -0.331      0.272   -1.22     0.22

visreg(m4,"Sex",by="AgeGroup")

Interaction between two numerical variables

saa$Age.z <- (saa$Age - mean(saa$Age)) / sd(saa$Age) 
summary(m5 <- lm(NL ~ LR.z * Age.z, data=saa)) # Instead of AgeGroup we use numerical Age


Call:
lm(formula = NL ~ LR.z * Age.z, data = saa)

Residuals:
   Min     1Q Median     3Q    Max 
-3.004 -0.670  0.116  0.670  2.237 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.0714     0.0623    1.15   0.2520    
LR.z          0.4763     0.0923    5.16  4.3e-07 ***
Age.z        -0.1752     0.0654   -2.68   0.0078 ** 
LR.z:Age.z   -0.1242     0.0561   -2.21   0.0277 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.959 on 321 degrees of freedom
Multiple R-squared:  0.0882,    Adjusted R-squared:  0.0796 
F-statistic: 10.3 on 3 and 321 DF,  p-value: 1.62e-06

Model comparison

summary(m5a <- lm(NL ~ LR.z + Age.z, data=saa))$coef # both significant

             Estimate Std. Error   t value Pr(>|t|)
(Intercept) -1.63e-16     0.0535 -3.05e-15 1.00e+00
LR.z         3.32e-01     0.0657  5.06e+00 7.11e-07
Age.z       -1.65e-01     0.0657 -2.52e+00 1.23e-02

anova(m5a, m5)

Analysis of Variance Table

Model 1: NL ~ LR.z + Age.z
Model 2: NL ~ LR.z * Age.z
  Res.Df RSS Df Sum of Sq    F Pr(>F)  
1    322 300                           
2    321 295  1       4.5 4.89  0.028 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interaction is significant

Question 6

Numerical variable better than nominal variable?

anova(m3, m5)

Analysis of Variance Table

Model 1: NL ~ LR.z * AgeGroup
Model 2: NL ~ LR.z * Age.z
  Res.Df RSS Df Sum of Sq F Pr(>F)
1    321 296                      
2    321 295  0     0.724

Both models are equally complex (same nr. of parameters), but m5 provides a better fit (RSS lower)
- Take note: it’s not a good idea to “simplify” numerical variables by converting to nominal variables!

Visual interpretation of the interaction (1)

visreg(m5, "LR.z", by="Age.z", overlay=TRUE)

Visual interpretation of the interaction (2)

visreg2d(m5, "LR.z", "Age.z")

library(rgl)
visreg2d(m5,"LR.z","Age.z",plot.type="rgl")

For comparison: the model without interaction

visreg(m5, "LR.z", by="Age.z", overlay=T)

visreg(m5a, "LR.z", by="Age.z", overlay=T)

Assumptions satisfied? (1/2)

library(car)

vif(m5) # determining VIF in a model with an interaction is a problem

there are higher-order terms (interactions) in this model
consider setting type = 'predictor'; see ?vif

      LR.z      Age.z LR.z:Age.z 
      3.00       1.51       2.39

vif(m5a) # therefore assess VIF in model without the interaction: OK!

 LR.z Age.z 
  1.5   1.5

Assumptions satisfied? (2/2)

par(mfrow=c(1,4))
qqnorm(resid(m5))
qqline(resid(m5)) # OK
plot(fitted(m), resid(m)) # NOT OK
plot(saa$LR.z, resid(m)) # NOT OK
plot(saa$Age.z, resid(m)) # NOT OK

Potential solutions of not satisfying the assumptions

Use an appropriate model
- Here we did not take into account variability associated with native language
- Mixed-effects regression is necessary for that
Make sure all important variables are included in the model
Transform the dependent variable (e.g., log-transformation)
Use a generalized linear regression model (which has fewer assumptions)
These potential solutions are not covered during this course (but in Statistiek II)

Part II: Questionnaires

Questionnaires are an easy way to obtain much data
But: how to ask the right question?
For example: How do students feel about statistics?
- What type of statistics?
- What kind of feelings?
For this reason, researchers ask several questions all aimed at acquiring similar information (i.e. questions are combined in a so-called scale)

Reliability and validity

Validity: are you measuring what you intend to measure?
- This can be checked by consulting experts, comparing to similar measures, etc.
Reliability: is your measure consistent?
- I.e. are results repeatable when obtained given the same conditions?
- This can be statistically assessed using Cronbach’s \(\alpha\)
Reliability \(\neq\) validity!

Question 7

Reliability and validity

Reliability: Cronbach’s \(\alpha\) (1)

Underlying idea:
- If we split the questions, how well do two halves of the questionnaire agree?
- And if there are many questions, how well would they agree if we looked at all possible ways of splitting?
More information: https://www.ijme.net/archive/2/cronbachs-alpha.pdf

Reliability: Cronbach’s \(\alpha\) (2)

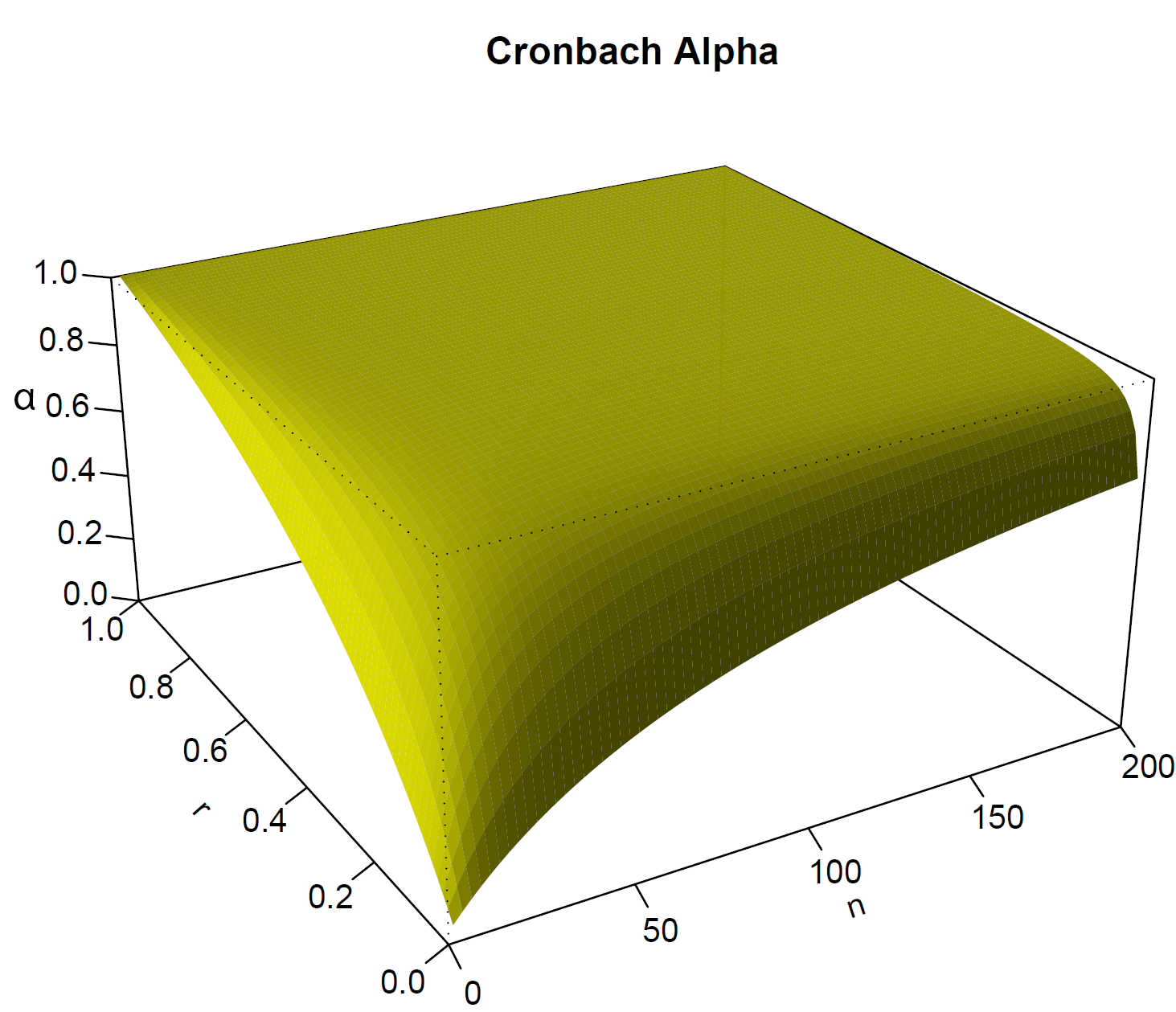
Cronbach’s \(\alpha\) depends on:
- The average correlation \(r\) of all variables (i.e. questions) involved
- The number of questions
Removing a problematic question may increase Cronbach’s \(\alpha\)
Cronbach’s \(\alpha\): > 0.7 is acceptable, 0.8 is good, 0.9 is very good
- With Cronbach’s \(\alpha\) > 0.7: mean of items can be used as summary of the scale

Cronbach’s \(\alpha\) depends on \(n\) and \(r\)

Questionnaire: your feelings toward statistics

Questions (in English): https://www.let.rug.nl/wieling/Statistiek-I/Final36scoring.pdf

load('sats.rda') 
head(sats) # scores 1-7: negative - positive (some inverted)

  Q3 Q4 Q14 Q15 Q18 Q19 Q28
1  7  2   6   2   2   6   1
2  4  4   3   4   4   4   4
3  3  3   6   6   5   2   6
4  5  4   6   4   3   6   2
5  4  5   6   4   4   2   5
6  4  2   6   2   3   5   2

Note that I have included one question which is part of a different scale
- We will try to identify this question later

Cronbach’s \(\alpha\) in R (1)

library(psych)
result <- alpha(sats) # normally you would simply use the command: alpha(sats)

Some items ( Q3 Q19 ) were negatively correlated with the first principal component and 
probably should be reversed.  
To do this, run the function again with the 'check.keys=TRUE' option

summary(result) # but only the output of summary fits on the slide


Reliability analysis   
 raw_alpha std.alpha G6(smc) average_r  S/N   ase mean   sd median_r
      0.41      0.37    0.63     0.078 0.59 0.039  4.2 0.69    0.042

Reliability is very low, but we ignored some questions having an inverted scale

Taking into account inverted questions

The instructions of the questionnaire show that questions 4, 15, 18 and 28 should be inverted (1 \(\rightarrow\) 7, 2 \(\rightarrow\) 6, 3 \(\rightarrow\) 5, 4 \(\rightarrow\) 4, etc.)

result <- alpha(sats, keys=c("Q4","Q15","Q18","Q28")) # keys: scales inverted
summary(result) # much better reliability


Reliability analysis   
 raw_alpha std.alpha G6(smc) average_r S/N   ase mean   sd median_r
      0.79      0.75    0.81       0.3   3 0.013  4.3 0.98     0.36

Can we improve reliability by dropping an item?

result$alpha.drop # note that the command alpha(sats) outputs this by default

     raw_alpha std.alpha G6(smc) average_r  S/N alpha se var.r med.r
Q3        0.74      0.69    0.73      0.27 2.18     0.02  0.10  0.36
Q4-       0.74      0.70    0.76      0.28 2.29     0.02  0.09  0.37
Q14       0.84      0.84    0.85      0.46 5.10     0.01  0.02  0.38
Q15-      0.77      0.73    0.80      0.31 2.67     0.01  0.12  0.37
Q18-      0.73      0.69    0.75      0.27 2.18     0.02  0.09  0.35
Q19       0.75      0.69    0.73      0.27 2.21     0.02  0.10  0.35
Q28-      0.71      0.67    0.73      0.26 2.06     0.02  0.08  0.35

Dropping Q14 would yield a higher Cronbach’s \(\alpha\)

Reliability without Q14

sats2 <- sats[,-3] # drop third column (Q14)
result2 <- alpha(sats2,keys=c("Q4","Q15","Q18","Q28")) # keys: scales inverted
summary(result2)


Reliability analysis   
 raw_alpha std.alpha G6(smc) average_r S/N   ase mean  sd median_r
      0.84      0.84    0.85      0.46 5.1 0.011    4 1.2     0.38

Question 8

Part III: Recap

In the following, an overview of the contents of the previous lectures is provided

What have we covered in the past lectures? (1)

Lecture 1: statistics and R
- Why use statistics?
- How to use R:
  - Variables, functions, importing data, viewing data, modifying data, visualization, and statistics
Lecture 2: descriptive statistics
- Four variable types
- Measures of central tendency and spread
- Standardized scores (\(z\)-scores)
- Distribution of a variable: normal distribution

What have we covered in the past lectures? (2)

Lecture 3: sampling
- Sample vs. population
  - Standard deviation for comparing individual to population
  - Standard error for comparing sample to population
- Definition of \(p\)-value (probability of data given hypothesis / probability of type-I error)
- Statistical significance (\(p\)-value vs. \(\alpha\)-value)
- Reasoning about population: confidence interval
- Reasoning about population: hypothesis tests (\(H_0\) vs. \(H_a\))
  - One-sided vs. two-sided hypothesis
- Comparing sample to population using standardized test: \(z\)-test
- Error types

What have we covered in the past lectures? (3)

Lecture 4: introduction to linear regression
- Correlation as descriptive statistic
- Simple linear regression with a single numerical predictor
  - Dependent (DV) vs. independent variable (IV)
  - Fitted values vs. residuals
  - Assumptions: residuals normally distributed and homoscedastic, linear relationship between IV and DV
  - Interpreting and visualizing output
- Effect size
- Reporting results

What have we covered in the past lectures? (4)

Lecture 5: (multiple) linear regression
- Simple linear regression with a single nominal predictor
- Multiple linear regression
  - Adding multiple independent variables
  - Additional assumption: no collinearity between IVs
  - Model comparison
  - Determining importance of independent variables
  - Interactions between two variables (introduction)

Recap

In this lecture, we’ve covered
- Interactions in multiple regression:
  - Interaction between a nominal and a numerical independent variable
  - Interaction between two nominal independent variables
  - Interaction between two numerical independent variables
- Cronbach’s alpha
Next lecture: Practice exam!

Please evaluate this lecture!

Exam question

Questions?

Thank you for your attention!

https://www.martijnwieling.nl

m.b.wieling@rug.nl