Self-similar structures

The intriguing pattern on this picture is a floor mosaic found  in the cathedral of Anagni (Italy). The cathedral and the floor were constructed in the year 1104 (information provided by Nicoletta Sala). It is a spectacular early example of what is known in mathematics as an iterative function system, a function that can be recursively iterated (repeated) to create fractal-like structures. The most important property of these functions is that they create self-similar structures, i.e., structures with parts that have the same form as the entire structure.  On the picture, you see that the biggest triangles contain the next biggest triangles, surrounded by three triangles of the same kind, containing the next biggest triangle, etc. This process can be infinitely repeated. 

If you find such structures and ideas complicated, just consider the following picture, which makes it all clear (with thanks to BU's math department):

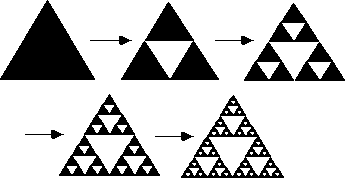
This picture shows how the triangle patterns, so-called Sierpinski triangles, are generated. There are even web sites with Java applets, which allow you to interactively generate these patterns.  Waclaw Sierpinski (1882-1969) was a prolific Polish mathematician specialized in number theory, who created and studied several self-similar patterns and the functions generating them. The triangles named after him are the most famous example. Fascinating as they are, Sierpinski triangles received much attention during the last few decades, thanks to the world-wide attention for fractals, as developed by Benoit Mandelbrot (1924-) and others. As I will show, the structure of our language falls in the general class of recursive, self-similar patterns, to which Sierpinski's triangles and Mandelbrot's fractals belong, too.

What I always find amazing is that profound mathematical patterns of this kind were often intuitively grasped in the decorative arts. Thus, medieval muslim artists intuitively discovered all 17 possible symmetry classes that are possible according to modern group algebra. Similarly, the unknown artist who designed the floor mosaics of the Anagni cathedral in 1104, intuitively realized the pattern reinvented and theoretically elucidated by Waclaw Sierpinski 800 years later!

It is becoming increasingly clear that self-similar structure is a design feature in the arts of almost all people, from Indian Hindu shrines to the hair styles and village designs of Africa (as shown by Ron Eglash in his book African Fractals: Modern Computing and Indigenous Design). All of this indicates that mathematical intuition is a universal property of the human mind, as explored in an exciting new field called ethnomathematics (see, for instance, Marcia Ascher, Ethnomathematics: A Multicultural View of Mathematical Ideas).

The mother of all self-similar structures is the pattern of human language. Natural languages have been described with recursive functions at least since the 1950s. However, initial applications of such ideas to many different languages led to a rather diverse and messy picture. Recent advances in theoretical linguistics indicate that the basic pattern is universal and extremely simple. As in the case of fractals, you can best appreciate the beauty and simplicity of the structure of language by visualizing it. Consider the structure of the simple phrase drinks for after dinner in English:

Clearly, the patterns of natural language are self-similar and iterative, like Sierpinski triangles and fractals. You see three main boxes, each consisting of exactly two parts, a blue part and a beige part. Linguists call this two-part structure binary branching. In each of the main boxes, the blue part is called the head and the beige part the complement. There is nothing mysterious about these notions. Examples of heads are just the word classes you used to learn in elementary school: nouns (like drinks), prepositions (like for and after), verbs (like see) and adjectives (like nice).

These words become a head as soon as they are put into a box (a phrase), where they can (potentially) be combined with other phrases (boxes in boxes). Thus, words listed in a dictionary are not heads. They only become a head in the context of phrases, the boxes you see above.

As you can observe in the structure, the blue heads are always on the left in English and the complements (boxes potentially containing more boxes) are always on the right. Linguists call that right branching.  Superficially,  you often find the opposite in  languages, ranging from Dutch to Japanese. Languages with such right-headed boxes would be left branching:

However, we have been able to show that in many cases such structures are only right-headed in appearance. The key, as I will show, is that certain boxes can be moved around in sentences according to fixed rules, which creates the illusion of the existence of a right-headed pattern (the second pattern above). We therefore hypothesize that all languages are left-headed with right-branching, like the first pattern above and that the second pattern is impossible. This hypothesis is more and more confirmed by recent research and reasoning. It is one of the most promising linguistic ideas around. 

All of this illustrates a fundamental property of linguistic building blocks, namely their left-right asymmetry. In the examples given, the heads are in a sense more prominent because the following complements depend on them. If you have the head, you can often predict what kind of complement follows. Head-complement structure is only one example of the fundamental left-right asymmetry. There are also cases, to be discussed later, in which the blue part is not a head but a "boxed" structure, like the complements. In all cases, however, the part on the right (beige) is dependent on the part on the left (blue). Both the blue part and the beige part can show the further recursion demonstrated with the boxes above:

Speaking in terms of these colored boxes, then, the structures of all languages are hypothesized to be made of the same building blocks: exactly one blue box (a head or a phrase), with exactly one dependent beige box (a head or a phrase) to its right. The word "etc." stands for the recursion: the asymmetric blue-beige pattern can infinitely be repeated in the positions taken by this word. The structure of natural language, in other words, consists of potentially infinite iterations of the same self-similar asymmetric pattern: one blue element followed by exactly one beige element.

Natural language could have "chosen" innumerable alternative box patterns to arrange its words in. However, nature seems to have given us exactly one possible pattern of box arrangement. If that's the case, you might ask, how do we then account for the apparent variation found in natural language? One of the major attractions of linguistics is that we seem to be able to reduce a multitude of seemingly different box patterns to the simple pattern given here.

Apart from its fundamental left-right asymmetry (blue-beige), the patterns as shown are also symmetrical: linearly speaking, we see a sequence of the same patterns along the left-right axis (as illustrated at the bottom of this page). This is called translation symmetry and it is combined with dilation symmetry: decrease of size of patterns of the same type, as in the Russian dolls. We see the same combination of translation symmetry and dilation in the fractal-like Sierpinski triangles, indicating that the structure of natural language is a specific but regular member of the broader family of recursive, self-similar structures.