Bertin's Classifier
Background
Jacques Bertin was the director of the cartographic laboratory at the
École à Pratique des Hautes Études who
specialized in the display of geographic information. He wrote
several of the classic texts on this topic, including in particular
Semiologie Graphique: Les Diagrammes, Les Reseaux, Les Cartes
(Mouton: Paris, 1967), one of the first systematic examinations of
the art and science of map-making.
Classification
But Bertin was not content with map-making, nor statistical graphics,
and not even with the static graphic representation of information.
In a further classic, La Graphique et le traitement graphique de
l'information (Flammarion: Paris, 1977) he advocated the use of
graphics in data exploration.
An example
On p.33 he introduces the problem of classifying communities of
varying sizes in France. He begins by noting nine properties together
with their realization (or lack thereof) in sixteen villages and towns
in France.

The properties he noted were the following:
- College presence in the town or village of a high school
- Cooperative Agriculture, presence of an agricultural cooperative
- Gare, presence of a train station
- École Classe Unique single-room elementary school
- Veterinaire veterinary
- Pas de Medecin lack of a local doctor
- Pas d'Adduction d'Eau lack of running water
- Gendarmerie presence of a police station
- Remembrement whether the town or village has been
Although he doesn't provide information about the sixteen communities
(in the columns A - P in the graphic), it is safe to say that it
is difficult to recognize a pattern in them. He sets himself the task
of classifying these communities along "natural" lines.
The Classifier
The mechanical classifier has only two basic operations, but both of
them are logically complex. The first operation "shuffles" rows,
aiming for an ordering in which similar rows are adjacent. The second
operation shuffles like columns, again with an aim toward a result in
which similar columns are next to each other. We first examine the
effect of reshuffling the rows.
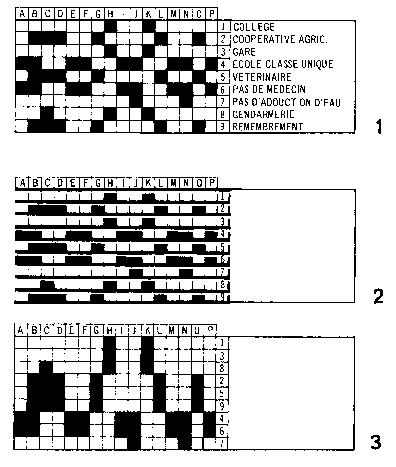
Notice what's happened here: the rows -- which, after all, occur in
arbitrary order, are simply reordered. In (3) the original row
numbers are retained so that you can examine the effect of the
reordering more exactly. In the first three rows of (3), one can see,
for example, that the properties 'high school', 'train station' and
'police station' seem to hold together of an individual community.
That is, they're either all present or none of them is in any given
community. With the exception of community C, which has only a
police statioin, it turns out that only H and K have any of these
facilities (in this data set), and they both have all of them. We can
summarize: the first step has identified similar properties.
Next, the same procedure is applied to the columns. They
likewise occur in arbitrary order, corresponding to the communities
in the original data set, which we might view in any order.
Reshuffling the columns, therefore, has the effect of grouping similar
communities -- completing the classification task which is the
purpose of the exercise.
Interpreting the Results
Even if the classification is complete, the result needs to be
examined to see if it is interpretable. In other words, we need to
check whether the results correspond to a useful classification.
Bertin does this in a final step, which merely labels the groups
which his classifier has identified.

A Software Realization
Peter Kleiweg has implemented a web version of the
classifier, including Bertin's example, but also the opportunity
to define one's own data sets.
Questions for Reflection
- In the final result, we can identify the groups in the
rows as well as in the columns. What in the process
is responsible for this?
- The classification is not perfect. Community C has
only one of the three "urban" properties, while A and B
both have two of the three rural properties and all of the
intermediate ones. Finally, most of the villages show only
two of the three the rural properties. Does this suggest
that the classifier isn't working properly, or do you
suppose that some rough edges are inherent in the task
of natural classification?
- Some properties are represented negatively, e.g., 'pas de
medecin' and pas d'adduction d'eau'. Using positive
versions of these properties instead of the negative ones would
seem to provide the same information, but how well would the
process work? Suggest ways in which the classifier could be
made more robust, i.e., less dependent on the form in
which information is provided.
- Bertin's choice of properties in this example was "fortunate"
-- they were all relevant to defining interesting classes.
Suppose he had included properties such as "has a street called
'Main Street' (Rue de Ville)", "has more women then men
inhabitants", or "is west of Paris" or other properties that
turn out to be less useful. What would these do to the
results? And what adjustments might be made to the classifier
to allow it to function even when irrelevant properties
are part of the input?
- All of Bertin's properties in this example are binary,
i.e., they either hold or do not hold of a given individual
(community). But other properites seem to be graded,
e.g., proximity to highway system, amount of traffic, number of
factories, etc. Speculate on what might be done to accommodate
someone who wished to see graded properties play a role in
classification.
- Kleiweg's software realization of Bertin's classifier has
no access to the visual presentation that Bertin uses.
Instead it counts fields with the same values in the rows
(or in the columns), and it later presents it's results
visually. Is it fair then to call this a visual technique?
- Bertin suggests his classifier is no longer useful when data
matrices (such as that in (1), which serves as input to the
process) becomes larger than 120 X 120 (p.31). Kleiweg's
software implementation also has a limited size. The software
might be optimized to deal with larger structures, but there is
probably a limit to what we can "see in a glance". Does this
suggest that graphic communication must be limited to
communicating only relatively simple information?
Return to
Graphic Communications Home page.




