The paper discusses the problem of determinising finite-state
automata containing large numbers of
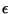
-moves. Experiments
with finite-state approximations of natural language grammars often
give rise to very large automata with a very large number of
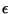
-moves. The paper identifies and compares a number of
subset construction algorithms which treat
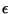
-moves.
Experiments have been performed which indicate that the algorithms
differ considerably in practice, both with respect to the size of
the resulting deterministic automaton, and with respect to practical
efficiency. Furthermore, the experiments suggest that the average
number of
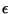
-moves per state can be used to predict which
algorithm is likely to be the fastest for a given input automaton.