Het formalisme $\cal {R}$($\cal {L}$)

In hoofdstuk 2 wordt een formalisme gedefinieerd dat in verschillende opzichten representatief is voor de formalismen die binnen de computationele taalkunde gebruikt worden. Het formalisme, $\cal {R}$($\cal {L}$), is gebaseerd op `constraints'. De constraints die gebruikt worden zijn de `path equations' (pad vergelijkingen) bekend van PATR II. Echter in het formalisme wordt niet voorgeschreven dat zinsdelen worden opgebouwd door middel van concatenatie, maar wordt de mogelijkheid opengehouden dat andere methoden gebruikt worden om zinsdelen samen te voegen. Het formalisme is dus te zien als een variant van puur Prolog, waarbij feature-strukturen de plaats van eerste orde termen overnemen. Bovendien wordt het formalisme gedefinieerd binnen het algemene kader van [32], waardoor het mogelijk is om krachtigere constraints aan het formalisme toe te voegen zonder dat bepaalde eigenschappen van het systeem verloren gaan, zolang de juiste `constraint-solving' technieken hiervoor beschikbaar zijn.

Het resulterende formalisme wordt in de dissertatie zowel gebruikt om grammatica's in te definiëren, als om `meta-interpreters' in te definiëren. Een grammatica in $\cal {R}$($\cal {L}$) is een `definite clause' specificatie van de relatie sign/1. Een simpel voorbeeld van een regel uit zo'n grammatica is de volgende clause:

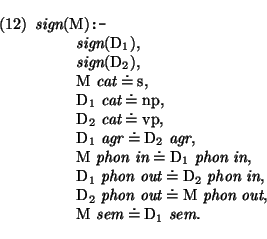
Zo'n regel wordt in de matrix notatie als volgt weergegeven:

De procedurele semantiek van $\cal {R}$($\cal {L}$) is vergelijkbaar met Prologs zoekmethode. Dat wil dus zeggen dat een refutatie van een `goal' plaats vindt volgens de `top-down' methode. De `computation rule' die wordt gebruikt selecteert steeds het meest linkse atoom. Daarnaast wordt de zoekruimte doorzocht met een `depth-first backtrack' strategie. Andere zoekprocedures worden later gedefinieerd in $\cal {R}$($\cal {L}$) als meta-interpretators.

Indien $\cal {R}$($\cal {L}$) gebruikt wordt om grammatica's in te definiëren dan wordt het p-parseer probleem als volgt gedefinieerd. Stel, de invoer voor het parseren is een feature structuur waarvan de fonologische structuur $\phi$ is als de waarde van het attribuut phon. De antwoorden op het phon-parseerprobleem zijn dan al die signs uit de grammatica die niet in tegenspraak zijn met de invoer, en bovendien ook $\phi$ als waarde voor hun phon attribuut hebben. Op dezelfde manier worden de antwoorden op het sem-parseerprobleem gedefinieerd als die signs uit de grammatica die compatibel zijn met de invoer, en dezelfde waarde hebben voor het sem attribuut.

In hoofdstuk 2 wordt aangetoond dat in zijn algemeenheid het p-parseer probleem voor $\cal {R}$($\cal {L}$) grammatica's onoplosbaar is, omdat het mogelijk is een onbeslisbaar probleem (Post's Correspondence Problem) te coderen als een $\cal {R}$($\cal {L}$) grammatica. Hieruit volgt dan ook onmiddellijk dat $\cal {R}$($\cal {L}$) grammatica's in zijn algemeenheid niet omkeerbaar zijn.

In de praktijk is het echter zo dat de grammatica's die door computationeel taalkundigen geschreven worden wel degelijk omkeerbaar zijn. Om deze reden is het dus een belangrijke taak bewijsprocedures te construeren die het p-parseer probleem oplossen voor de grammatica's die in de praktijk gebruikt blijken te worden. Deze taak beslaat het belangrijkste deel van deze dissertatie (de hoofdstukken 3 en 4). In deze hoofdstukken worden genereer- en parseertechnieken ontwikkeld die ruimer toepasbaar zijn dan sommige andere methoden. Bovendien worden deze technieken gemotiveerd vanuit een taalkundig oogpunt omdat bepaalde `head-driven' en lexicalistische eigenschappen van moderne grammatica's uitgebuit worden, in de hoop dat dit zal leiden tot een grotere efficientie.