Top-down generators and left recursion


next up previous
Next: Shieber's chart-based generator Up: Problems with early Previous: Problems with early

Top-down generators and left recursion

To illustrate the principal problem for top-down generators I will define a very simple top-down generator in . Assume that grammars are defined as clauses of the form 

Node ---> Nodes

where is a term of the form ; is a -list of such nodes. 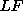represents the logical form; is a difference-list represention of the string and can be any term representing syntactic information. As an example consider the following grammar. png

  

node(s/LF,P0-PN) --->                  % s rule
    [ node(Np,P0-P1), 
      node(vp(Np,[])/LF,P1-PN) ].

node(vp(Subj,T)/LF,P0-PN) --->         % vp complementation
    [ node(vp(Subj,[Obj|T])/LF,P0-P1), 
      node(Obj,P1-PN) ].

node(np/LF,P0-PN) --->                 % np rule
    [ node(det/LF,P0-P1),
      node(n/LF,P1-PN) ].

node(np/john,[john|X]-X) ---> 
    [].                                % john
node(np/mary,[mary|X]-X) ---> 
    [].                                % mary
node(n/boy,[boy|X]-X) ---> 
    [].                                % boy
node(n/girl,[girl|X]-X) --->    
    [].                                % girl
node(det/_,[the|X]-X) ---> 
    [].                                % the

node(vp(np/Np,[])/sleep(Np),           % to sleep
    [sleeps|X]-X) ---> [].

node(vp(np/Np,[np/Np2])/               % to kiss
    kisses(Np,Np2),[kisses|X]-X) ---> [].

node(vp(np/Np,[np/Np2,p/up])/          % to call up
    call_up(Np,Np2),[calls|X]-X) ---> [].

node(p/up,[up|X]-X) ---> [].           % up

A suitable parser for this simple grammar will instantiate 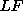in the call

to . Note that in this grammar a lot of `interesting' feature percolations are defined in the lexical entries. Now consider the `naive' top-down generation algorithm:

  

generate(LF,String) :- 
    gen(node(_/LF,String-[]).

gen(Node) :- 
    ( Node ---> Nodes ), 
    gen_ds(Nodes).

gen_ds([]).
gen_ds([Node|Nodes]) :- 
    gen(Node), 
    gen_ds(Nodes).

The algorithm simply matches a node with the mother node of some rule and recursively generates the daughters of this rule. Because of the left to right search strategy of this algorithm will not terminate if we give it the semantics , because when it applies rule , it will try to generate a node with an unknown logical form and an unknown syntactic category. The algorithm thus will apply rule for this node, and will go into an infinite loop because each time it chooses rule for the first daughter of rule .

Therefore, the order in which nonterminals are expanded is very important, as was noticed in [31][7]. If in the foregoing example the generator first tries to generate the second daughter, then the first daughter can be generated without problems afterwards. In the approach of Dymetman and Isabelle the order of generation is defined by the rule-writer by annotating rules. In the approach of Wedekind this ordering is achieved automatically by essentially a version of the goal-freezing technique [6]. Put simply, the generator only generates a node if its logical form is instantiated; otherwise the generator will try to generate other nodes first.

A specific version of the first approach is an approach where one of the daughters has a privileged status. This daughter, that we might call the `head' of the rule will always be generated first. The notion `head' may be defined by the rule writer or by some other method. I will simply asssume that for all rules the first daughter of the list of daughters represents the head png. For example, the 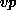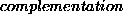rule will now look as follows: 

node(vp(Subj,T)/LF,P0-PN) --->        % vp complementation
    [ node(vp(Subj,[Obj|T])/LF,P0-P1), node(Obj,P1-PN) ].

Now without any modification to the original definition of this change will imply that heads are generated first.

The resulting simple top-down generation algorithm is equivalent to the approaches of [7] and [31] with respect to one major problem: the left-recursion problem.

Suppose this generator tries to generate a sentence for the logical form . As required the generator will first try to generate a verb phrase after the selection of rule , assuming that the second daughter is appropriately chosen as the head. However, to generate this verb phrase the generator will try to apply the 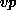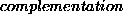rule. For this rule to apply it will try to apply the same rule for its first daughter. Each time the same rule can be applied (predicting longer and longer lists of complements), resulting in non termination, because of left recursion.

Now the question is whether this problem is a linguistically relevant problem. According to Klaus Netter (personal communication) the foregoing type of rules can not be written in LFG and therefore Wedekind's generator has been used without any problems for LFG-grammars. 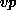I want to argue that at least for linguistic theories such as UCG, other versions of unification based categorial grammars and some versions of HPSG left-recursive rules such as the 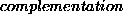rule occur very frequently. Moreover in [23][30] we have argued at length that the problem can not be solved by an ad-hoc restriction on the length of this list of complements. Several Germanic languages require rules where this list of complements can grow during a derivation (in case of cross-serial dependencies) without a linguistically motivated upper bound. The conclusion of this section therefore is that top-down generators have problems with some linguistically motivated left recursive analyses png.


next up previous
Next: Shieber's chart-based generator Up: Problems with early Previous: Problems with early


Gertjan van Noord
Fri Nov 25 13:07:08 MET 1994