---
title : Crash course in R
subtitle :
author : Martijn Wieling
job : Computational Linguistics Research Group
framework : io2012 # {io2012, html5slides, shower, dzslides, ...}
theme : neon
highlighter : highlight.js # {highlight.js, prettify, highlight}
hitheme : tomorrow #
widgets : [mathjax] # {mathjax, quiz, bootstrap}
ext_widgets: {rCharts: [libraries/nvd3]}
mode : selfcontained # {standalone, draft}
knit : slidify::knit2slides
biglogo : rug.png
logo : rug.png
---
## This lecture
* RStudio and R
* R as calculator
* Variables
* Functions and help
* Importing data in R in a dataframe
* Accessing rows and columns
* Adding columns to the data
* Data exploration
* Numerical measures
* Visual exploration
* Data analysis: statistical tests
---
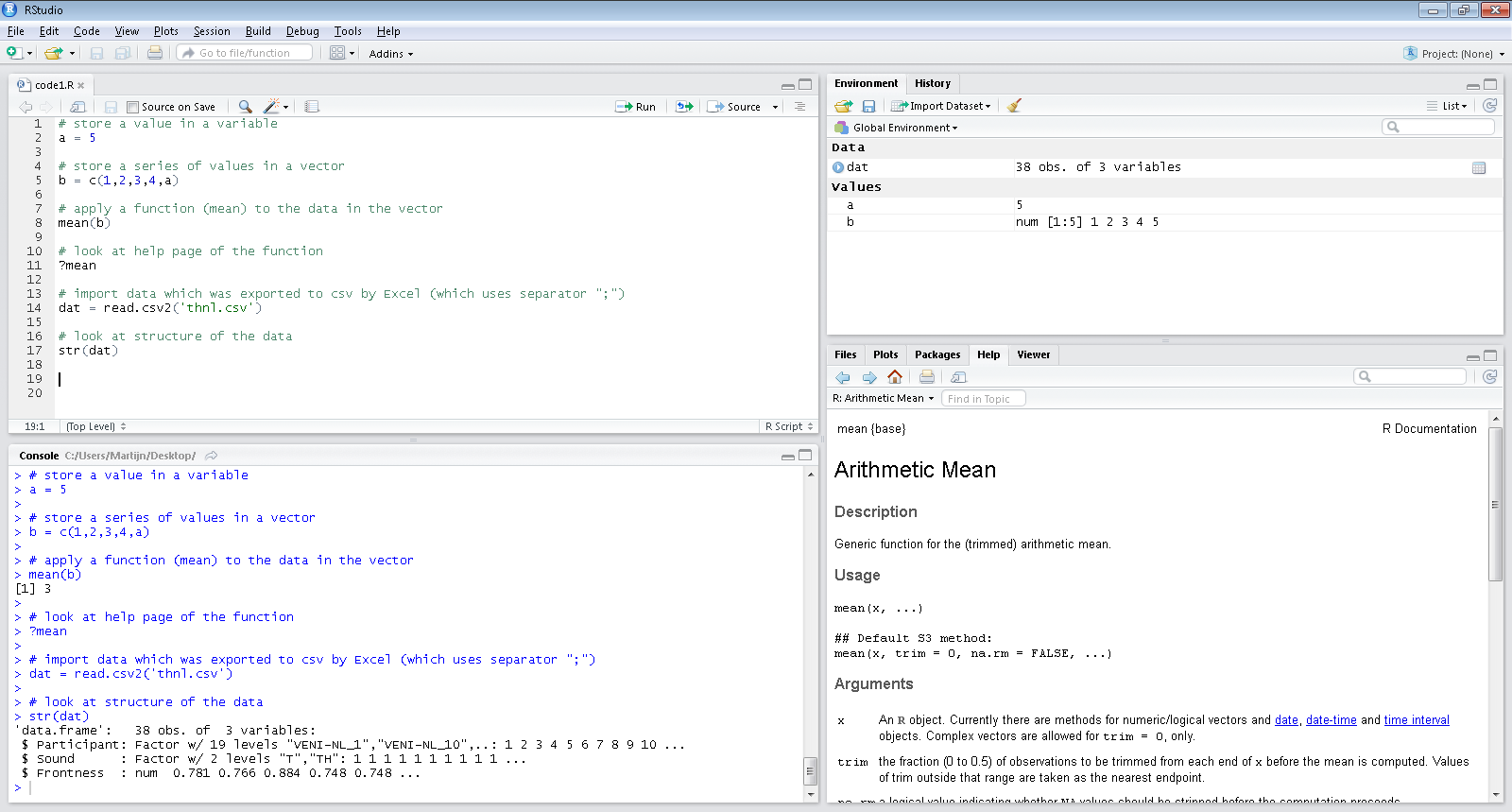
## Our tool: RStudio (frontend to R)
---
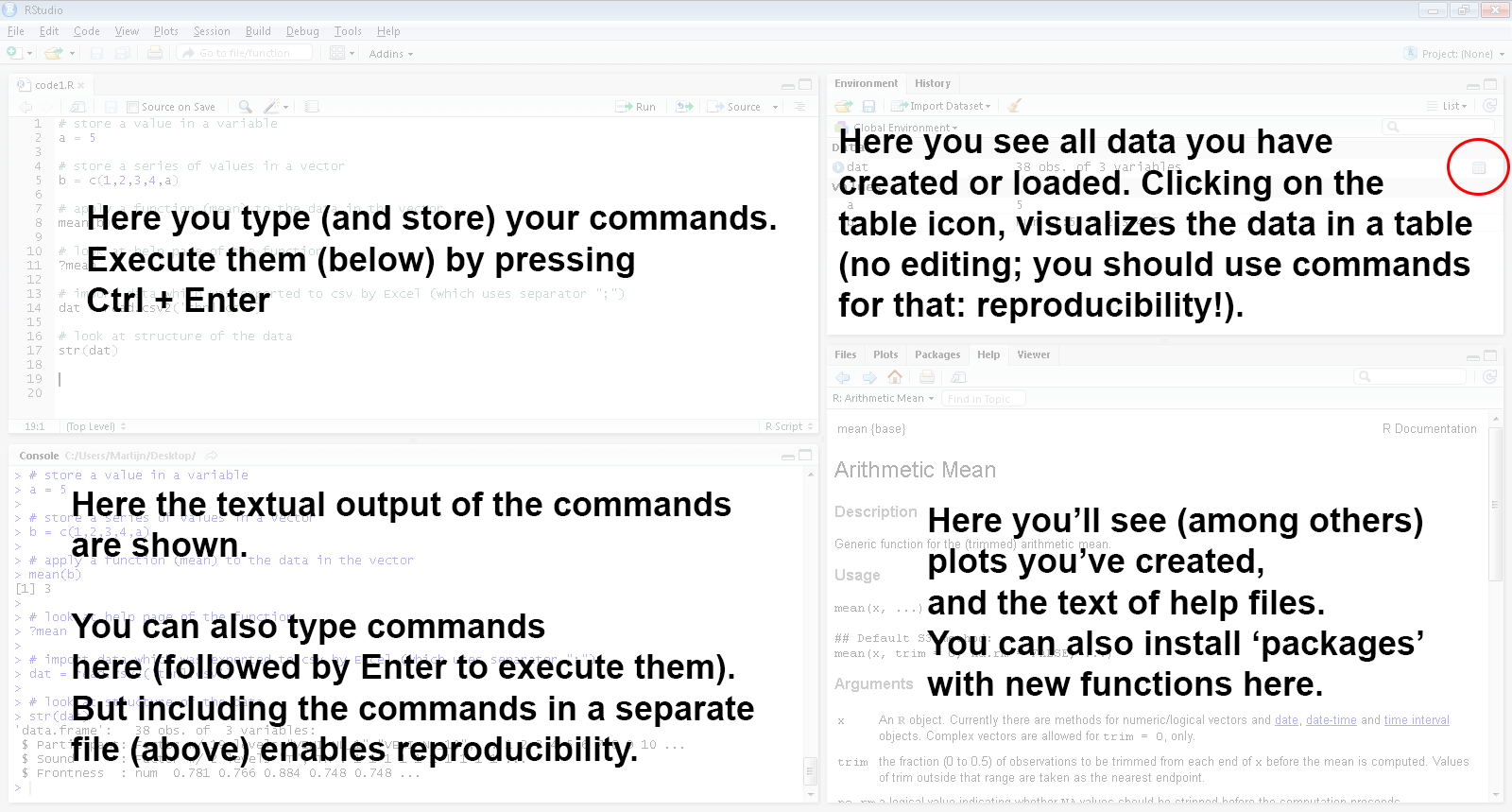
## RStudio: quick overview
---
## Basic functionality: R as calculator
```r
# Addition (this is a comment: preceded by '#')
5 + 5
```
```
# [1] 10
```
```r
# Multiplication
5 * 3
```
```
# [1] 15
```
```r
# Division
5/3
```
```
# [1] 1.6667
```
---
## Basic functionality: using variables
```r
a <- 5 # store a single value; instead of '<-' you can also use '='
a # display the value
```
```
# [1] 5
```
```r
b <- c(2, 4, 6, 7, 8) # store a series of values in a vector
b
```
```
# [1] 2 4 6 7 8
```
```r
b[4] <- a # assign value 5 (stored in 'a') to the 4th element of vector b
b[1] <- NA # assign NA (missing) to the first element of vector b
b <- b * 10 # multiply all values in vector b with 10
b
```
```
# [1] NA 40 60 50 80
```
---
## Question 1
---
## Basic functionality: using functions
```r
mn <- mean(b) # calculating the mean and storing in variable mn
mn
```
```
# [1] NA
```
```r
# mn is NA (missing) as one of the values is missing
mean(b, na.rm = TRUE) # we can use the function parameter na.rm to ignore NAs
```
```
# [1] 57.5
```
```r
# But which parameters does a function have: use help!
help(mean) # alternatively: ?mean
```
---
## Basic functionality: a help file
---
## Question 2
---
## Try it yourself!
* There are many resources for R which you can easily find online
* Here we use "swirl" an online platform for creating and using interactive R courses
* Start RStudio, install and start swirl:
```r
install.packages("swirl", repos = "http://cran.rstudio.com/")
library(swirl)
swirl()
```
* Follow the prompts and install the course *R programming: The basics of programming in R*
* Choose that course to start with and finish *Lesson 1* of that course
---
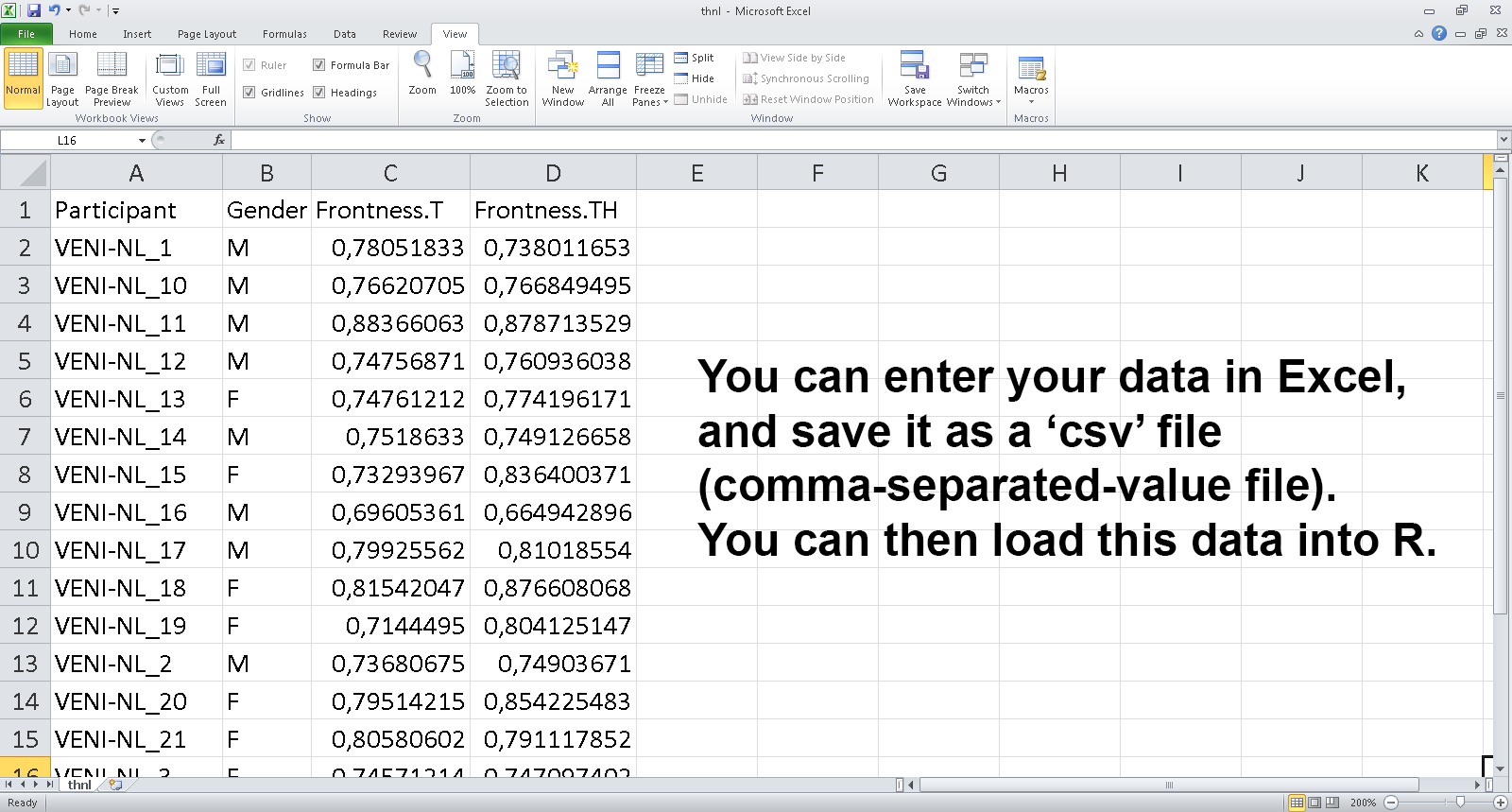
## Getting data into R: exporting a data set
---
## Getting data into R: importing a data set
```r
# first set directory to where file is located, e.g., using function setwd()
dat <- read.csv2("thnl.csv") # read.csv2 reads Excel csv file from work dir
str(dat) # shows structure of the data frame dat (note: wide format)
```
```
# 'data.frame': 19 obs. of 4 variables:
# $ Participant : Factor w/ 19 levels "VENI-NL_1","VENI-NL_10",..: 1 2 3 4 5 6 7 8 9 10 ...
# $ Gender : Factor w/ 2 levels "F","M": 2 2 2 2 2 2 1 2 2 1 ...
# $ Frontness.T : num 0.781 0.766 0.884 0.748 0.748 ...
# $ Frontness.TH: num 0.738 0.767 0.879 0.761 0.774 ...
```
```r
dim(dat) # number of rows and columns of data set
```
```
# [1] 19 4
```
---
## Investigating imported data set: using head
```r
head(dat) # show first few rows of dat
```
```
# Participant Gender Frontness.T Frontness.TH
# 1 VENI-NL_1 M 0.78052 0.73801
# 2 VENI-NL_10 M 0.76621 0.76685
# 3 VENI-NL_11 M 0.88366 0.87871
# 4 VENI-NL_12 M 0.74757 0.76094
# 5 VENI-NL_13 M 0.74761 0.77420
# 6 VENI-NL_14 M 0.75186 0.74913
```
---
## Question 3
---
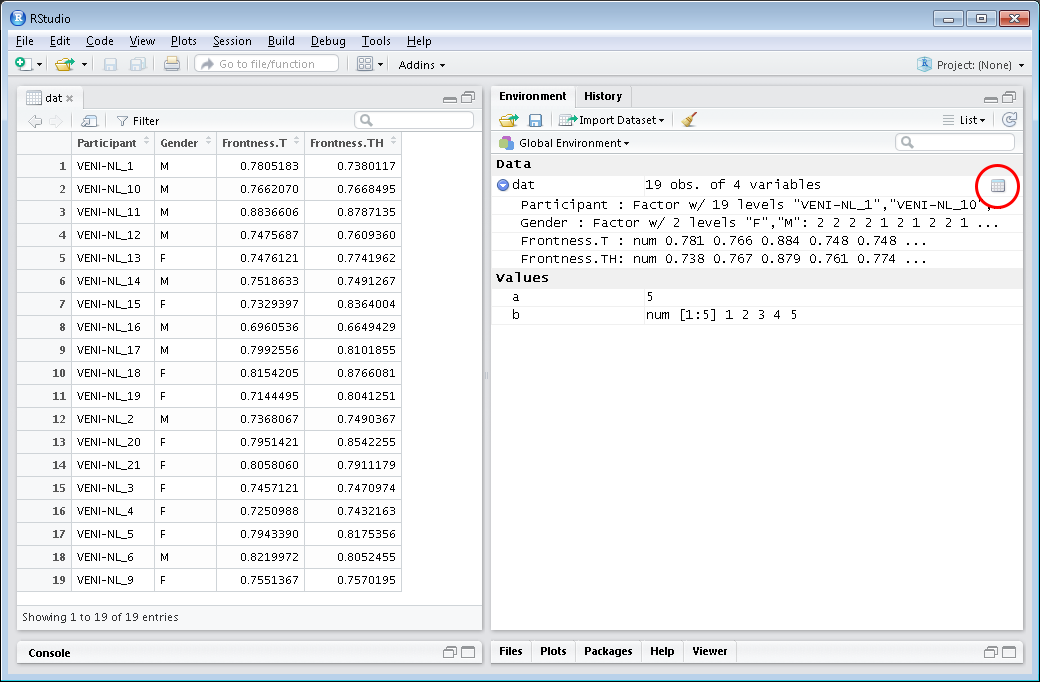
## Investigating imported data set: using RStudio viewer
---
## Subsetting the data: indices and names
```r
dat[1, ] # values in first row
```
```
# Participant Gender Frontness.T Frontness.TH
# 1 VENI-NL_1 M 0.78052 0.73801
```
```r
dat[1:2, c(2, 3)] # values of first two rows for second and third column
```
```
# Gender Frontness.T
# 1 M 0.78052
# 2 M 0.76621
```
```r
dat[c(1, 2, 3), "Participant"] # values of first three rows for column 'Participant'
```
```
# [1] VENI-NL_1 VENI-NL_10 VENI-NL_11
# 19 Levels: VENI-NL_1 VENI-NL_10 VENI-NL_11 VENI-NL_12 VENI-NL_13 VENI-NL_14 ... VENI-NL_9
```
```r
tmp <- dat[5:8, c(1, 3)] # store columns 1 and 3 for rows 5 to 8 in tmp
```
---
## Question 4
---
## Subsetting the data: conditional indexing
```r
tmp <- dat[dat$Gender == "M", ] # only observations for male participants
head(tmp, n = 2) # show first two rows
```
```
# Participant Gender Frontness.T Frontness.TH
# 1 VENI-NL_1 M 0.78052 0.73801
# 2 VENI-NL_10 M 0.76621 0.76685
```
```r
# more advanced subsetting: include rows for which frontness for the T sound is
# higher than 0.74 AND participant is either 1 or 2 N.B. use '|' instead of '&'
# for logical OR
dat[dat$Frontness.T > 0.74 & dat$Participant %in% c("VENI-NL_1", "VENI-NL_2"), ]
```
```
# Participant Gender Frontness.T Frontness.TH
# 1 VENI-NL_1 M 0.78052 0.73801
```
---
## Question 5
---
## Supplementing the data: adding columns
```r
# new column Diff containing difference between TH and T positions
dat$Diff <- dat$Frontness.TH - dat$Frontness.T
# new column DiffClass, initially all observations set to TH0
dat$DiffClass <- "TH0"
# observations with Diff larger than 0.02 are categorized as TH1, negative as TH-
dat[dat$Diff > 0.02, ]$DiffClass <- "TH1"
dat[dat$Diff < 0, ]$DiffClass <- "TH-"
dat$DiffClass <- factor(dat$DiffClass) # convert string variable to factor
head(dat, 2)
```
```
# Participant Gender Frontness.T Frontness.TH Diff DiffClass
# 1 VENI-NL_1 M 0.78052 0.73801 -0.04250668 TH-
# 2 VENI-NL_10 M 0.76621 0.76685 0.00064245 TH0
```
---
## Question 6
---
## Try it yourself!
* Run swirl() in RStudio and finish the following lessons of the *R Programming* course:
* *Lesson 6*: Subsetting vectors
* *Lesson 12*: Looking at data
---
## Numerical variables: central tendency and spread
```r
mean(dat$Diff) # mean
```
```
# [1] 0.016263
```
```r
median(dat$Diff) # median
```
```
# [1] 0.01093
```
```r
min(dat$Diff) # minimum value
```
```
# [1] -0.042507
```
```r
max(dat$Diff) # maximum value
```
```
# [1] 0.10346
```
---
## Numerical variables: measures of spread
```r
sd(dat$Diff) # standard deviation
```
```
# [1] 0.038213
```
```r
var(dat$Diff) # variance
```
```
# [1] 0.0014603
```
```r
quantile(dat$Diff) # quantiles
```
```
# 0% 25% 50% 75% 100%
# -0.0425067 -0.0038419 0.0109299 0.0248903 0.1034607
```
---
## Categorical variables: frequency tables
```r
table(dat$Gender)
```
```
#
# F M
# 9 10
```
```r
table(dat$DiffClass)
```
```
#
# TH- TH0 TH1
# 6 7 6
```
---
## Question 7
---
## Exploring relationships between pairs of variables
```r
# correlation: two numerical variables
cor(dat$Frontness.T, dat$Frontness.TH)
```
```
# [1] 0.71054
```
```r
# crosstable: two categorical variables
table(dat$Gender, dat$DiffClass)
```
```
#
# TH- TH0 TH1
# F 1 3 5
# M 5 4 1
```
```r
# means per category: numerical and categorical variable
c(mean(dat[dat$Gender == "M", ]$Diff), mean(dat[dat$Gender == "F", ]$Diff))
```
```
# [1] -0.0034299 0.0381446
```
---
## Question 8
---
## Data exploration with visualization
* Many basic visualization options are available in R
* boxplot() for a boxplot
* hist() for a histogram
* qqnorm() and qqline() for a quantile-quantile plot
* plot() for many types of plots (scatter, line, etc.)
* barplot() for a barplot (plotting frequencies)
---
## Exploring numerical variables: box plot
```r
par(mfrow = c(1, 2)) # set graphics option: 2 graphs side-by-side
boxplot(dat$Diff, main = "Difference") # boxplot of difference values
boxplot(dat[, c("Frontness.T", "Frontness.TH")]) # frontness per group
```
 ---
## Exploring numerical variables: histogram
```r
hist(dat$Diff, main = "Difference histogram")
```
---
## Exploring numerical variables: histogram
```r
hist(dat$Diff, main = "Difference histogram")
```
 ---
## Exploring numerical variables: Q-Q plot
```r
qqnorm(dat$Diff) # plot actual values vs. theoretical quantiles
qqline(dat$Diff) # plot reference line of normal distribution
```
---
## Exploring numerical variables: Q-Q plot
```r
qqnorm(dat$Diff) # plot actual values vs. theoretical quantiles
qqline(dat$Diff) # plot reference line of normal distribution
```
 ---
## Exploring numerical relations: scatter plot
```r
plot(dat$Frontness.T, dat$Frontness.TH, col = "blue")
```
---
## Exploring numerical relations: scatter plot
```r
plot(dat$Frontness.T, dat$Frontness.TH, col = "blue")
```
 ---
## Visualizing categorical variables (frequencies): bar plot
```r
counts <- table(dat$Gender) # frequency table for gender
barplot(counts, ylim = c(0, 15))
```
---
## Visualizing categorical variables (frequencies): bar plot
```r
counts <- table(dat$Gender) # frequency table for gender
barplot(counts, ylim = c(0, 15))
```
 ---
## Exploring categorical relations: segmented bar plot
```r
counts <- table(dat$Gender, dat$DiffClass)
barplot(counts, col = c("pink", "lightblue"), legend = rownames(counts), ylim = c(0,
10))
```
---
## Exploring categorical relations: segmented bar plot
```r
counts <- table(dat$Gender, dat$DiffClass)
barplot(counts, col = c("pink", "lightblue"), legend = rownames(counts), ylim = c(0,
10))
```
 ---
## Question 9
---
## Try it yourself!
* Run
---
## Question 9
---
## Try it yourself!
* Run swirl() in RStudio and finish the following lesson of the *R Programming* course:
* *Lesson 15*: Base graphics
---
## Basic statistical functionality in R
* Most basic statistical functions are available in R
* t.test() for a $t$-test (single sample, paired, independent)
* wilcox.test() for non-parametric alternatives to the $t$-test
* chisq.test() for the chi-square test
* aov() for one-way ANOVA
* lm() for regression
* Note: in all subsequent analyses, I'm assuming that the assumptions for the tests are met (i.e. normal distribution and/or homogeneous variances)
---
## Assumptions of statistical tests: normality (1)
* For investigating normality, a Q-Q plot should be used
```r
qqnorm(dat$Diff) # plot actual values vs. theoretical quantiles
qqline(dat$Diff) # plot reference line of normal distribution
```
 ---
## Assumptions of statistical tests: normality (2)
* Alternatively, one can use the Shapiro-Wilk test of normality
* But note that the test is sensitive to sample size
```r
shapiro.test(dat$Diff)
```
```
#
# Shapiro-Wilk normality test
#
# data: dat$Diff
# W = 0.92, p-value = 0.11
```
---
## Assumptions of statistical tests: homoscedasticity (1)
* Testing homoscedasticity using Bartlett Test (requires normality)
* Levene's test is more robust to departures of normality, but is not present in the default installation of
---
## Assumptions of statistical tests: normality (2)
* Alternatively, one can use the Shapiro-Wilk test of normality
* But note that the test is sensitive to sample size
```r
shapiro.test(dat$Diff)
```
```
#
# Shapiro-Wilk normality test
#
# data: dat$Diff
# W = 0.92, p-value = 0.11
```
---
## Assumptions of statistical tests: homoscedasticity (1)
* Testing homoscedasticity using Bartlett Test (requires normality)
* Levene's test is more robust to departures of normality, but is not present in the default installation of R
* It is available in the add-on package car, which contains other useful functions and will be discussed later
```r
bartlett.test(list(dat[dat$Gender == "M", ]$Diff, dat[dat$Gender == "F", ]$Diff))
```
```
#
# Bartlett test of homogeneity of variances
#
# data: list(dat[dat$Gender == "M", ]$Diff, dat[dat$Gender == "F", ]$Diff)
# Bartlett's K-squared = 3.42, df = 1, p-value = 0.064
```
```r
# simpler way to write this: bartlett.test( Diff ~ Gender, data=dat )
```
---
## Assumptions of statistical tests: homoscedasticity (2)
* Testing homoscedasticity using the Fligner-Killeen median test (robust to departures from normality)
```r
fligner.test(Diff ~ Gender, data = dat)
```
```
#
# Fligner-Killeen test of homogeneity of variances
#
# data: Diff by Gender
# Fligner-Killeen:med chi-squared = 2.79, df = 1, p-value = 0.095
```
---
## Group mean vs. value: single sample $t$-test (1)
```r
# start with visualization
boxplot(dat$Diff)
abline(h = 0, col = "red")
```
 ---
## Group mean vs. value: single sample $t$-test (2)
```r
t.test(dat$Diff) # 2-tailed test is default
```
```
#
# One Sample t-test
#
# data: dat$Diff
# t = 1.86, df = 18, p-value = 0.08
# alternative hypothesis: true mean is not equal to 0
# 95 percent confidence interval:
# -0.002155 0.034682
# sample estimates:
# mean of x
# 0.016263
```
```r
t.test(dat$Diff, alternative = "greater")$p.value # 1-tailed p-value
```
```
# [1] 0.040018
```
---
## Try it yourself!
* Install the *Mathematical Biostatistics Boot Camp* swirl course:
```r
library(swirl)
install_from_swirl("Mathematical_Biostatistics_Boot_Camp")
```
* Run
---
## Group mean vs. value: single sample $t$-test (2)
```r
t.test(dat$Diff) # 2-tailed test is default
```
```
#
# One Sample t-test
#
# data: dat$Diff
# t = 1.86, df = 18, p-value = 0.08
# alternative hypothesis: true mean is not equal to 0
# 95 percent confidence interval:
# -0.002155 0.034682
# sample estimates:
# mean of x
# 0.016263
```
```r
t.test(dat$Diff, alternative = "greater")$p.value # 1-tailed p-value
```
```
# [1] 0.040018
```
---
## Try it yourself!
* Install the *Mathematical Biostatistics Boot Camp* swirl course:
```r
library(swirl)
install_from_swirl("Mathematical_Biostatistics_Boot_Camp")
```
* Run swirl() in RStudio and finish the following lesson of the *Mathematical Biostatistics Boot Camp* course:
* *Lesson 1*: One sample t-test
---
## Comparing paired data: paired samples $t$-test (1)
```r
# start with visualization
boxplot(dat[, c("Frontness.T", "Frontness.TH")])
```
 ---
## Comparing paired data: paired samples $t$-test (2)
```r
t.test(dat$Frontness.T, dat$Frontness.TH, paired = TRUE)
```
```
#
# Paired t-test
#
# data: dat$Frontness.T and dat$Frontness.TH
# t = -1.86, df = 18, p-value = 0.08
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -0.034682 0.002155
# sample estimates:
# mean of the differences
# -0.016263
```
```r
t.test(dat$Frontness.T, dat$Frontness.TH, paired = T, alt = "greater")$p.value # wrong tail!
```
```
# [1] 0.95998
```
---
## Comparing two groups: indep. samples $t$-test (1)
```r
# start with visualization
boxplot(Diff ~ Gender, data = dat)
```
---
## Comparing paired data: paired samples $t$-test (2)
```r
t.test(dat$Frontness.T, dat$Frontness.TH, paired = TRUE)
```
```
#
# Paired t-test
#
# data: dat$Frontness.T and dat$Frontness.TH
# t = -1.86, df = 18, p-value = 0.08
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -0.034682 0.002155
# sample estimates:
# mean of the differences
# -0.016263
```
```r
t.test(dat$Frontness.T, dat$Frontness.TH, paired = T, alt = "greater")$p.value # wrong tail!
```
```
# [1] 0.95998
```
---
## Comparing two groups: indep. samples $t$-test (1)
```r
# start with visualization
boxplot(Diff ~ Gender, data = dat)
```
 ---
## Comparing two groups: indep. samples $t$-test (2)
```r
t.test(dat[dat$Gender == "M", ]$Diff, dat[dat$Gender == "F", ]$Diff) # default: unequal var.
```
```
#
# Welch Two Sample t-test
#
# data: dat[dat$Gender == "M", ]$Diff and dat[dat$Gender == "F", ]$Diff
# t = -2.68, df = 11.6, p-value = 0.02
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -0.0754351 -0.0077139
# sample estimates:
# mean of x mean of y
# -0.0034299 0.0381446
```
```r
t.test(dat[dat$Gender == "M", ]$Diff, dat[dat$Gender == "F", ]$Diff, var.equal = TRUE)$p.value
```
```
# [1] 0.013018
```
---
## Question 10 (final)
---
## Non-parametric alternatives
* Should be used when assumptions of $t$-test violated
* Values or differences normally distributed with $n < 15$
* No large skew or outliers with $n < 40$
* Non-parametric fallbacks
* One sample $t$-test and paired $t$-test: Wilcoxon signed rank
* Independent samples $t$-test: Mann-Whitney U test (= Wilcoxon rank sum test)
* In both cases:
---
## Comparing two groups: indep. samples $t$-test (2)
```r
t.test(dat[dat$Gender == "M", ]$Diff, dat[dat$Gender == "F", ]$Diff) # default: unequal var.
```
```
#
# Welch Two Sample t-test
#
# data: dat[dat$Gender == "M", ]$Diff and dat[dat$Gender == "F", ]$Diff
# t = -2.68, df = 11.6, p-value = 0.02
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
# -0.0754351 -0.0077139
# sample estimates:
# mean of x mean of y
# -0.0034299 0.0381446
```
```r
t.test(dat[dat$Gender == "M", ]$Diff, dat[dat$Gender == "F", ]$Diff, var.equal = TRUE)$p.value
```
```
# [1] 0.013018
```
---
## Question 10 (final)
---
## Non-parametric alternatives
* Should be used when assumptions of $t$-test violated
* Values or differences normally distributed with $n < 15$
* No large skew or outliers with $n < 40$
* Non-parametric fallbacks
* One sample $t$-test and paired $t$-test: Wilcoxon signed rank
* Independent samples $t$-test: Mann-Whitney U test (= Wilcoxon rank sum test)
* In both cases: wilcox.test
---
## Group mean vs. value: Wilcoxon signed rank (1)
```r
# start with visualization
qqnorm(dat$Diff)
qqline(dat$Diff)
```
 ---
## Group mean vs. value: Wilcoxon signed rank (2)
```r
wilcox.test(dat$Diff) # 2-tailed test is default
```
```
#
# Wilcoxon signed rank test
#
# data: dat$Diff
# V = 133, p-value = 0.13
# alternative hypothesis: true location is not equal to 0
```
```r
wilcox.test(dat$Diff, alternative = "greater")$p.value # 1-tailed p-value
```
```
# [1] 0.066811
```
---
## Comparing paired data: Wilcoxon signed rank
```r
wilcox.test(dat$Frontness.T, dat$Frontness.TH, paired = TRUE)
```
```
#
# Wilcoxon signed rank test
#
# data: dat$Frontness.T and dat$Frontness.TH
# V = 57, p-value = 0.13
# alternative hypothesis: true location shift is not equal to 0
```
```r
wilcox.test(dat$Frontness.T, dat$Frontness.TH, paired = T, alternative = "less")$p.value
```
```
# [1] 0.066811
```
---
## Comparing two groups: Mann-Whitney U test (1)
```r
par(mfrow = c(1, 2)) # start with visualization
qqnorm(dat[dat$Gender == "M", ]$Diff, main = "M")
qqline(dat[dat$Gender == "M", ]$Diff)
qqnorm(dat[dat$Gender == "F", ]$Diff, main = "F")
qqline(dat[dat$Gender == "F", ]$Diff)
```
---
## Group mean vs. value: Wilcoxon signed rank (2)
```r
wilcox.test(dat$Diff) # 2-tailed test is default
```
```
#
# Wilcoxon signed rank test
#
# data: dat$Diff
# V = 133, p-value = 0.13
# alternative hypothesis: true location is not equal to 0
```
```r
wilcox.test(dat$Diff, alternative = "greater")$p.value # 1-tailed p-value
```
```
# [1] 0.066811
```
---
## Comparing paired data: Wilcoxon signed rank
```r
wilcox.test(dat$Frontness.T, dat$Frontness.TH, paired = TRUE)
```
```
#
# Wilcoxon signed rank test
#
# data: dat$Frontness.T and dat$Frontness.TH
# V = 57, p-value = 0.13
# alternative hypothesis: true location shift is not equal to 0
```
```r
wilcox.test(dat$Frontness.T, dat$Frontness.TH, paired = T, alternative = "less")$p.value
```
```
# [1] 0.066811
```
---
## Comparing two groups: Mann-Whitney U test (1)
```r
par(mfrow = c(1, 2)) # start with visualization
qqnorm(dat[dat$Gender == "M", ]$Diff, main = "M")
qqline(dat[dat$Gender == "M", ]$Diff)
qqnorm(dat[dat$Gender == "F", ]$Diff, main = "F")
qqline(dat[dat$Gender == "F", ]$Diff)
```
 ---
## Comparing two groups: Mann-Whitney U test (2)
```r
wilcox.test(dat[dat$Gender == "F", ]$Diff, dat[dat$Gender == "M", ]$Diff)
```
```
#
# Wilcoxon rank sum test
#
# data: dat[dat$Gender == "F", ]$Diff and dat[dat$Gender == "M", ]$Diff
# W = 73, p-value = 0.022
# alternative hypothesis: true location shift is not equal to 0
```
---
## Dependency between two cat. variables: $\chi^2$ test (1)
```r
chisq.test(table(dat$Gender, dat$DiffClass)) # warning due to low expected values
```
```
# Warning in chisq.test(table(dat$Gender, dat$DiffClass)): Chi-squared approximation may be incorrect
```
```
#
# Pearson's Chi-squared test
#
# data: table(dat$Gender, dat$DiffClass)
# X-squared = 5.44, df = 2, p-value = 0.066
```
```r
table(dat$Gender, dat$DiffClass)
```
```
#
# TH- TH0 TH1
# F 1 3 5
# M 5 4 1
```
---
## Dependency between two cat. variables: $\chi^2$ test (2)
```r
chisq.test(table(dat$Gender, dat$DiffClass), simulate.p.value = TRUE)
```
```
#
# Pearson's Chi-squared test with simulated p-value (based on 2000 replicates)
#
# data: table(dat$Gender, dat$DiffClass)
# X-squared = 5.44, df = NA, p-value = 0.086
```
---
## Differences between 3+ groups: one-way ANOVA (1)
```r
# start with visualization
boxplot(Diff ~ DiffClass, data = dat)
```
---
## Comparing two groups: Mann-Whitney U test (2)
```r
wilcox.test(dat[dat$Gender == "F", ]$Diff, dat[dat$Gender == "M", ]$Diff)
```
```
#
# Wilcoxon rank sum test
#
# data: dat[dat$Gender == "F", ]$Diff and dat[dat$Gender == "M", ]$Diff
# W = 73, p-value = 0.022
# alternative hypothesis: true location shift is not equal to 0
```
---
## Dependency between two cat. variables: $\chi^2$ test (1)
```r
chisq.test(table(dat$Gender, dat$DiffClass)) # warning due to low expected values
```
```
# Warning in chisq.test(table(dat$Gender, dat$DiffClass)): Chi-squared approximation may be incorrect
```
```
#
# Pearson's Chi-squared test
#
# data: table(dat$Gender, dat$DiffClass)
# X-squared = 5.44, df = 2, p-value = 0.066
```
```r
table(dat$Gender, dat$DiffClass)
```
```
#
# TH- TH0 TH1
# F 1 3 5
# M 5 4 1
```
---
## Dependency between two cat. variables: $\chi^2$ test (2)
```r
chisq.test(table(dat$Gender, dat$DiffClass), simulate.p.value = TRUE)
```
```
#
# Pearson's Chi-squared test with simulated p-value (based on 2000 replicates)
#
# data: table(dat$Gender, dat$DiffClass)
# X-squared = 5.44, df = NA, p-value = 0.086
```
---
## Differences between 3+ groups: one-way ANOVA (1)
```r
# start with visualization
boxplot(Diff ~ DiffClass, data = dat)
```
 ---
## Differences between 3+ groups: one-way ANOVA (2)
```r
result <- aov(Diff ~ DiffClass, data = dat)
# non-parametric alternative: kruskal.test(Diff ~ DiffClass, dat=dat)
summary(result) # is the ANOVA significant?
```
```
# Df Sum Sq Mean Sq F value Pr(>F)
# DiffClass 2 0.01957 0.00978 23.3 1.8e-05 ***
# Residuals 16 0.00672 0.00042
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
---
## ANOVA post-hoc test
```r
TukeyHSD(result) # post-hoc tests
```
```
# Tukey multiple comparisons of means
# 95% family-wise confidence level
#
# Fit: aov(formula = Diff ~ DiffClass, data = dat)
#
# $DiffClass
# diff lwr upr p adj
# TH0-TH- 0.027155 -0.0022602 0.056571 0.07281
# TH1-TH- 0.079321 0.0487957 0.109847 0.00001
# TH1-TH0 0.052166 0.0227509 0.081582 0.00086
```
--- .smallcode
## Relating numerical variables: linear regression
```r
result <- lm(Frontness.T ~ Frontness.TH, data = dat)
summary(result) # predictor significant
```
```
#
# Call:
# lm(formula = Frontness.T ~ Frontness.TH, data = dat)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.06674 -0.01274 -0.00056 0.01169 0.05867
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.299 0.113 2.65 0.01692 *
# Frontness.TH 0.598 0.144 4.16 0.00065 ***
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# Residual standard error: 0.0325 on 17 degrees of freedom
# Multiple R-squared: 0.505, Adjusted R-squared: 0.476
# F-statistic: 17.3 on 1 and 17 DF, p-value: 0.000651
```
---
## Linear regression: residuals normally distributed?
```r
modelResiduals <- resid(result)
qqnorm(modelResiduals)
qqline(modelResiduals) # not really
```
---
## Differences between 3+ groups: one-way ANOVA (2)
```r
result <- aov(Diff ~ DiffClass, data = dat)
# non-parametric alternative: kruskal.test(Diff ~ DiffClass, dat=dat)
summary(result) # is the ANOVA significant?
```
```
# Df Sum Sq Mean Sq F value Pr(>F)
# DiffClass 2 0.01957 0.00978 23.3 1.8e-05 ***
# Residuals 16 0.00672 0.00042
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
---
## ANOVA post-hoc test
```r
TukeyHSD(result) # post-hoc tests
```
```
# Tukey multiple comparisons of means
# 95% family-wise confidence level
#
# Fit: aov(formula = Diff ~ DiffClass, data = dat)
#
# $DiffClass
# diff lwr upr p adj
# TH0-TH- 0.027155 -0.0022602 0.056571 0.07281
# TH1-TH- 0.079321 0.0487957 0.109847 0.00001
# TH1-TH0 0.052166 0.0227509 0.081582 0.00086
```
--- .smallcode
## Relating numerical variables: linear regression
```r
result <- lm(Frontness.T ~ Frontness.TH, data = dat)
summary(result) # predictor significant
```
```
#
# Call:
# lm(formula = Frontness.T ~ Frontness.TH, data = dat)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.06674 -0.01274 -0.00056 0.01169 0.05867
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.299 0.113 2.65 0.01692 *
# Frontness.TH 0.598 0.144 4.16 0.00065 ***
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# Residual standard error: 0.0325 on 17 degrees of freedom
# Multiple R-squared: 0.505, Adjusted R-squared: 0.476
# F-statistic: 17.3 on 1 and 17 DF, p-value: 0.000651
```
---
## Linear regression: residuals normally distributed?
```r
modelResiduals <- resid(result)
qqnorm(modelResiduals)
qqline(modelResiduals) # not really
```
 --- .smallcode
## Relating num. and cat. variables: linear regression
```r
result <- lm(Diff ~ DiffClass + Frontness.TH + Gender, data = dat)
summary(result) # not all predictors significant
```
```
#
# Call:
# lm(formula = Diff ~ DiffClass + Frontness.TH + Gender, data = dat)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.03746 -0.00878 -0.00120 0.00813 0.04020
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -0.11795 0.08439 -1.40 0.18398
# DiffClassTH0 0.02612 0.01165 2.24 0.04165 *
# DiffClassTH1 0.06575 0.01473 4.46 0.00053 ***
# Frontness.TH 0.13805 0.10710 1.29 0.21828
# GenderM -0.00876 0.01102 -0.80 0.43971
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# Residual standard error: 0.0202 on 14 degrees of freedom
# Multiple R-squared: 0.783, Adjusted R-squared: 0.722
# F-statistic: 12.7 on 4 and 14 DF, p-value: 0.000145
```
--- .smallcode
## Linear regression: choosing the best model
```r
m0 <- lm(Diff ~ 1, data = dat)
m1 <- lm(Diff ~ DiffClass, data = dat)
m2 <- lm(Diff ~ DiffClass + Frontness.TH, data = dat)
m3 <- lm(Diff ~ DiffClass + Frontness.TH + Gender, data = dat)
anova(m0, m1, m2, m3) # model comparison: m1 best model
```
```
# Analysis of Variance Table
#
# Model 1: Diff ~ 1
# Model 2: Diff ~ DiffClass
# Model 3: Diff ~ DiffClass + Frontness.TH
# Model 4: Diff ~ DiffClass + Frontness.TH + Gender
# Res.Df RSS Df Sum of Sq F Pr(>F)
# 1 18 0.02628
# 2 16 0.00672 2 0.01957 24.06 3e-05 ***
# 3 15 0.00595 1 0.00077 1.89 0.19
# 4 14 0.00569 1 0.00026 0.63 0.44
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
---
## Extended statistical functionality in R: packages
* Not all functionality is available in the default installation of
--- .smallcode
## Relating num. and cat. variables: linear regression
```r
result <- lm(Diff ~ DiffClass + Frontness.TH + Gender, data = dat)
summary(result) # not all predictors significant
```
```
#
# Call:
# lm(formula = Diff ~ DiffClass + Frontness.TH + Gender, data = dat)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.03746 -0.00878 -0.00120 0.00813 0.04020
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -0.11795 0.08439 -1.40 0.18398
# DiffClassTH0 0.02612 0.01165 2.24 0.04165 *
# DiffClassTH1 0.06575 0.01473 4.46 0.00053 ***
# Frontness.TH 0.13805 0.10710 1.29 0.21828
# GenderM -0.00876 0.01102 -0.80 0.43971
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# Residual standard error: 0.0202 on 14 degrees of freedom
# Multiple R-squared: 0.783, Adjusted R-squared: 0.722
# F-statistic: 12.7 on 4 and 14 DF, p-value: 0.000145
```
--- .smallcode
## Linear regression: choosing the best model
```r
m0 <- lm(Diff ~ 1, data = dat)
m1 <- lm(Diff ~ DiffClass, data = dat)
m2 <- lm(Diff ~ DiffClass + Frontness.TH, data = dat)
m3 <- lm(Diff ~ DiffClass + Frontness.TH + Gender, data = dat)
anova(m0, m1, m2, m3) # model comparison: m1 best model
```
```
# Analysis of Variance Table
#
# Model 1: Diff ~ 1
# Model 2: Diff ~ DiffClass
# Model 3: Diff ~ DiffClass + Frontness.TH
# Model 4: Diff ~ DiffClass + Frontness.TH + Gender
# Res.Df RSS Df Sum of Sq F Pr(>F)
# 1 18 0.02628
# 2 16 0.00672 2 0.01957 24.06 3e-05 ***
# 3 15 0.00595 1 0.00077 1.89 0.19
# 4 14 0.00569 1 0.00026 0.63 0.44
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
---
## Extended statistical functionality in R: packages
* Not all functionality is available in the default installation of R
* Functionality can be added by installing (once) and loading a package with new functions:
* Post-hoc tests for linear regression (package multcomp)
* Multi-way ANOVA and ANCOVA (package car)
* Linear mixed-effects regression (package lme4)
* Converting data to 1 row per observation (long format; package reshape)
* Generally searching online for a specific functionality yields a suitable package (e.g., ggplot2 for advanced plotting functions)
* For example:
```r
install.packages("lme4", repos = "http://cran.rstudio.com/") # installation only once
library(lme4) # then load package
```
--- .smallcode
## Post-hoc tests for linear regression
```r
library(multcomp) # install via: install.packages('multcomp')
summary(glht(m1, linfct = mcp(DiffClass = "Tukey")))
```
```
#
# Simultaneous Tests for General Linear Hypotheses
#
# Multiple Comparisons of Means: Tukey Contrasts
#
#
# Fit: lm(formula = Diff ~ DiffClass, data = dat)
#
# Linear Hypotheses:
# Estimate Std. Error t value Pr(>|t|)
# TH0 - TH- == 0 0.0272 0.0114 2.38 0.073 .
# TH1 - TH- == 0 0.0793 0.0118 6.71 <0.001 ***
# TH1 - TH0 == 0 0.0522 0.0114 4.58 <0.001 ***
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# (Adjusted p values reported -- single-step method)
```
---
## Multi-way ANOVA: first some remarks
* When the data is unbalanced (as it is here) there are different methods to calculate the sum-of-squares
* We'll use Type 3 SS here, as this is what SPSS uses
* Type 3 SS requires contrasts to be orthogonal, which needs to be set explicitly as this is different from the default setting in R
* If the data is balanced (i.e. the same number of observations for each combination of factors), the different types all give the same results
---
## Present data not balanced
```r
table(dat$Gender, dat$DiffClass)
```
```
#
# TH- TH0 TH1
# F 1 3 5
# M 5 4 1
```
---
## Interaction plot
```r
with(dat, interaction.plot(DiffClass, Gender, Diff, col = c("blue", "red"), type = "b"))
```
 --- .smallcode
## Multi-way ANOVA
```r
library(car)
# set orthogonal contrasts contrasts for unordered and ordered factors
op <- options(contrasts = c("contr.sum", "contr.poly"))
Anova(aov(Diff ~ DiffClass * Gender, data = dat), type = 3) # run Anova SS type 3
```
```
# Anova Table (Type III tests)
#
# Response: Diff
# Sum Sq Df F value Pr(>F)
# (Intercept) 0.00194 1 4.75 0.0484 *
# DiffClass 0.00700 2 8.57 0.0042 **
# Gender 0.00063 1 1.55 0.2346
# DiffClass:Gender 0.00106 2 1.30 0.3054
# Residuals 0.00531 13
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
```r
options(op) # reset to previous setting (treatment contrasts for unordered factors)
```
--- .smallcode
## ANCOVA: adding Frontness.T as a covariate
```r
library(car)
op <- options(contrasts = c("contr.sum", "contr.poly"))
Anova(aov(Diff ~ DiffClass * Gender + Frontness.T, data = dat), type = 3)
```
```
# Anova Table (Type III tests)
#
# Response: Diff
# Sum Sq Df F value Pr(>F)
# (Intercept) 0.00028 1 0.65 0.4370
# DiffClass 0.00623 2 7.30 0.0084 **
# Gender 0.00068 1 1.60 0.2304
# Frontness.T 0.00019 1 0.44 0.5178
# DiffClass:Gender 0.00118 2 1.39 0.2869
# Residuals 0.00512 12
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
```r
options(op)
```
---
## Converting wide format to long format
```r
library(reshape)
datlong <- melt(dat, id.vars=c("Participant","Gender","Diff","DiffClass"),
measure.vars= c("Frontness.T","Frontness.TH"), variable_name="Type")
head(datlong,3)
```
```
# Participant Gender Diff DiffClass Type value
# 1 VENI-NL_1 M -0.04250668 TH- Frontness.T 0.78052
# 2 VENI-NL_10 M 0.00064245 TH0 Frontness.T 0.76621
# 3 VENI-NL_11 M -0.00494710 TH- Frontness.T 0.88366
```
```r
dim(dat)
```
```
# [1] 19 6
```
```r
dim(datlong)
```
```
# [1] 38 6
```
--- .smallcode
## Mixed-effects regression
```r
library(lme4)
model <- lmer(value ~ Gender + DiffClass + (1 | Participant), data = datlong)
summary(model, cor = F)
```
```
# Linear mixed model fit by REML ['lmerMod']
# Formula: value ~ Gender + DiffClass + (1 | Participant)
# Data: datlong
#
# REML criterion at convergence: -110.7
#
# Scaled residuals:
# Min 1Q Median 3Q Max
# -1.8897 -0.2849 -0.0311 0.4311 1.7146
#
# Random effects:
# Groups Name Variance Std.Dev.
# Participant (Intercept) 0.001732 0.0416
# Residual 0.000824 0.0287
# Number of obs: 38, groups: Participant, 19
#
# Fixed effects:
# Estimate Std. Error t value
# (Intercept) 0.78476 0.02824 27.79
# GenderM -0.00501 0.02518 -0.20
# DiffClassTH0 -0.02403 0.02659 -0.90
# DiffClassTH1 0.01299 0.03156 0.41
```
---
## Recap
* In this lecture, we've covered the basics of
--- .smallcode
## Multi-way ANOVA
```r
library(car)
# set orthogonal contrasts contrasts for unordered and ordered factors
op <- options(contrasts = c("contr.sum", "contr.poly"))
Anova(aov(Diff ~ DiffClass * Gender, data = dat), type = 3) # run Anova SS type 3
```
```
# Anova Table (Type III tests)
#
# Response: Diff
# Sum Sq Df F value Pr(>F)
# (Intercept) 0.00194 1 4.75 0.0484 *
# DiffClass 0.00700 2 8.57 0.0042 **
# Gender 0.00063 1 1.55 0.2346
# DiffClass:Gender 0.00106 2 1.30 0.3054
# Residuals 0.00531 13
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
```r
options(op) # reset to previous setting (treatment contrasts for unordered factors)
```
--- .smallcode
## ANCOVA: adding Frontness.T as a covariate
```r
library(car)
op <- options(contrasts = c("contr.sum", "contr.poly"))
Anova(aov(Diff ~ DiffClass * Gender + Frontness.T, data = dat), type = 3)
```
```
# Anova Table (Type III tests)
#
# Response: Diff
# Sum Sq Df F value Pr(>F)
# (Intercept) 0.00028 1 0.65 0.4370
# DiffClass 0.00623 2 7.30 0.0084 **
# Gender 0.00068 1 1.60 0.2304
# Frontness.T 0.00019 1 0.44 0.5178
# DiffClass:Gender 0.00118 2 1.39 0.2869
# Residuals 0.00512 12
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```
```r
options(op)
```
---
## Converting wide format to long format
```r
library(reshape)
datlong <- melt(dat, id.vars=c("Participant","Gender","Diff","DiffClass"),
measure.vars= c("Frontness.T","Frontness.TH"), variable_name="Type")
head(datlong,3)
```
```
# Participant Gender Diff DiffClass Type value
# 1 VENI-NL_1 M -0.04250668 TH- Frontness.T 0.78052
# 2 VENI-NL_10 M 0.00064245 TH0 Frontness.T 0.76621
# 3 VENI-NL_11 M -0.00494710 TH- Frontness.T 0.88366
```
```r
dim(dat)
```
```
# [1] 19 6
```
```r
dim(datlong)
```
```
# [1] 38 6
```
--- .smallcode
## Mixed-effects regression
```r
library(lme4)
model <- lmer(value ~ Gender + DiffClass + (1 | Participant), data = datlong)
summary(model, cor = F)
```
```
# Linear mixed model fit by REML ['lmerMod']
# Formula: value ~ Gender + DiffClass + (1 | Participant)
# Data: datlong
#
# REML criterion at convergence: -110.7
#
# Scaled residuals:
# Min 1Q Median 3Q Max
# -1.8897 -0.2849 -0.0311 0.4311 1.7146
#
# Random effects:
# Groups Name Variance Std.Dev.
# Participant (Intercept) 0.001732 0.0416
# Residual 0.000824 0.0287
# Number of obs: 38, groups: Participant, 19
#
# Fixed effects:
# Estimate Std. Error t value
# (Intercept) 0.78476 0.02824 27.79
# GenderM -0.00501 0.02518 -0.20
# DiffClassTH0 -0.02403 0.02659 -0.90
# DiffClassTH1 0.01299 0.03156 0.41
```
---
## Recap
* In this lecture, we've covered the basics of R
* Now you should be able (with help of this presentation) to use R for:
* Data manipulation
* Data exploration
* Data visualization
* Data analysis
* Your turn to try!
* http://www.let.rug.nl/wieling/statscourse/CrashCourseR/lab
---
## More about advanced statistical analysis in R
* http://www.let.rug.nl/wieling/statscourse
* Lectures 1 and 2: Mixed-effects regression
* Lectures 3, 4 and 5: Generalized additive modeling (i.e. non-linear regression)
---
## Evaluation
--- {
tpl: thankyou,
social: [{title: www, href: "http://www.martijnwieling.nl"}, {title: eml, href: "wieling@gmail.com"}]
}
## Questions?
Thank you for your attention!