---
title : Mixed-effects regression and eye-tracking data
subtitle : Lecture 2 of advanced regression for linguists
author : Martijn Wieling
job : Department of Information Science
framework : io2012 # {io2012, html5slides, shower, dzslides, ...}
theme : neon
highlighter : highlight.js # {highlight.js, prettify, highlight}
hitheme : tomorrow #
widgets : [mathjax] # {mathjax, quiz, bootstrap}
ext_widgets: {rCharts: [libraries/nvd3]}
mode : selfcontained # {standalone, draft}
knit : slidify::knit2slides
biglogo : rug.png
logo : rug.png
---
## This lecture
* Introduction
* Gender processing in Dutch
* Eye-tracking to reveal gender processing
* Design
* Analysis
* Conclusion
---
## Gender processing in Dutch
* The goal of this study is to investigate if Dutch people use grammatical gender to anticipate upcoming words
* This study was conducted together with Hanneke Loerts and is published in the Journal of Psycholinguistic Research (Loerts, Wieling and Schmid, 2012)
* What is grammatical gender?
* Gender is a property of a noun
* Nouns are divided into classes: masculine, feminine, neuter, ...
* E.g., hond ('dog') = common, paard ('horse') = neuter
* The gender of a noun can be determined from the forms of other elements syntactically related to it (Matthews, 1997: 36)
---
## Gender in Dutch
* Gender in Dutch: 70% common, 30% neuter
* When a noun is diminutive it is always neuter
* Gender is unpredictable from the root noun and hard to learn
---
## Why use eye tracking?
* Eye tracking reveals incremental processing of the listener during the time course of the speech signal
* As people tend to look at what they hear (Cooper, 1974), lexical competition can be tested
---
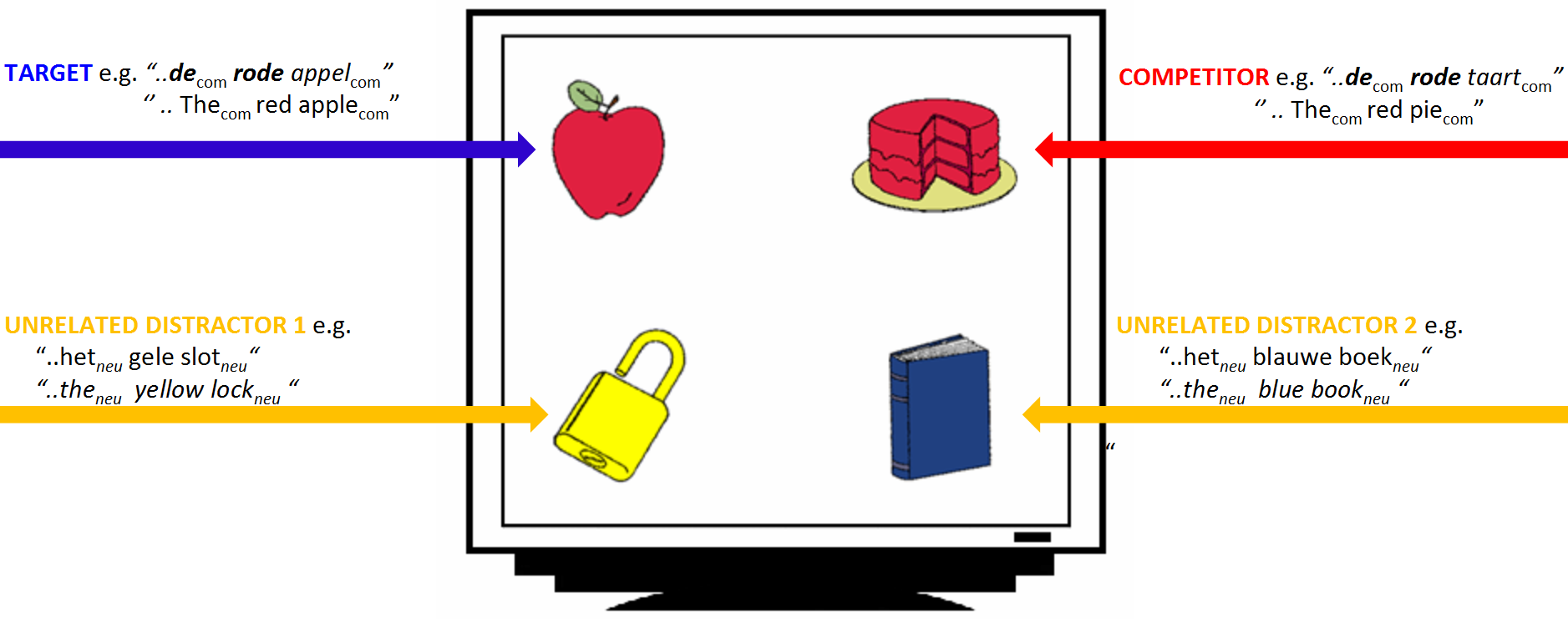
## Testing lexical competition using eye tracking
* Cohort Model (Marslen-Wilson & Welsh, 1978): Competition between words is based on word-initial activation
* This can be tested using the visual world paradigm: following eye movements while participants receive auditory input to click on one of several objects on a screen
---
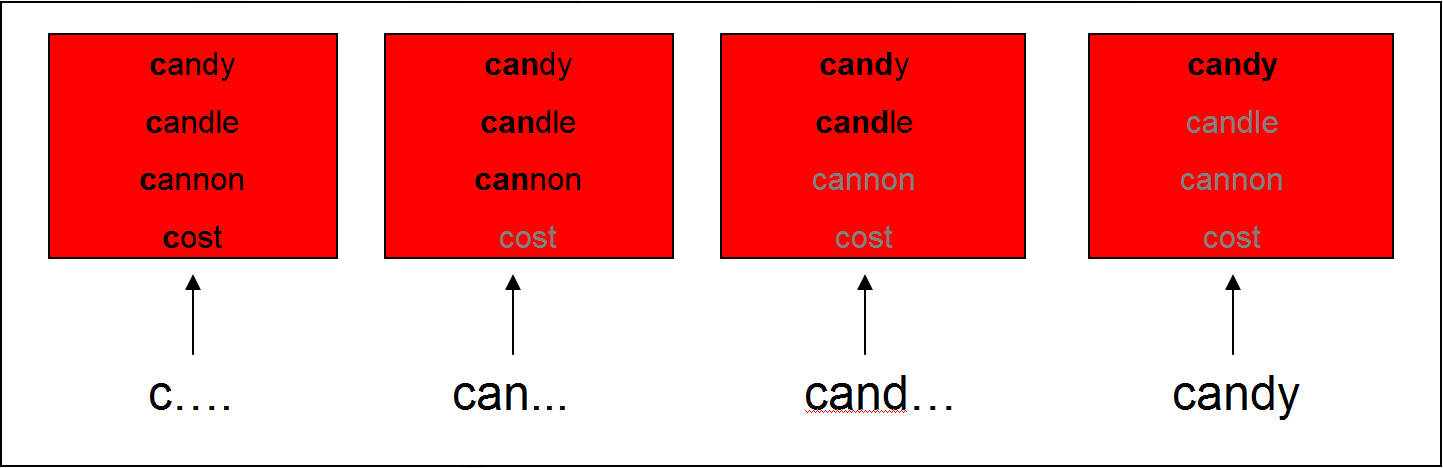
## Support for the Cohort Model
* Subjects hear: "Pick up the candy" (Tanenhaus et al., 1995)
* Fixations towards target (Candy) and competitor (Candle): support for the Cohort Model
---
## Lexical competition based on syntactic gender
* Other models of lexical processing state that lexical competition occurs based on all acoustic input (e.g., TRACE, Shortlist, NAM)
* Does gender information restrict the possible set of lexical candidates?
* I.e. if you hear de, will you focus more on an image of a dog (de hond) than on an image of a horse (het paard)?
* Previous studies (e.g., Dahan et al., 2000 for French) have indicated gender information restricts the possible set of lexical candidates
* In the following, we will investigate if this also holds for Dutch with its difficult gender system using the visual world paradigm
* We analyze the data using mixed-effects regression in R
---
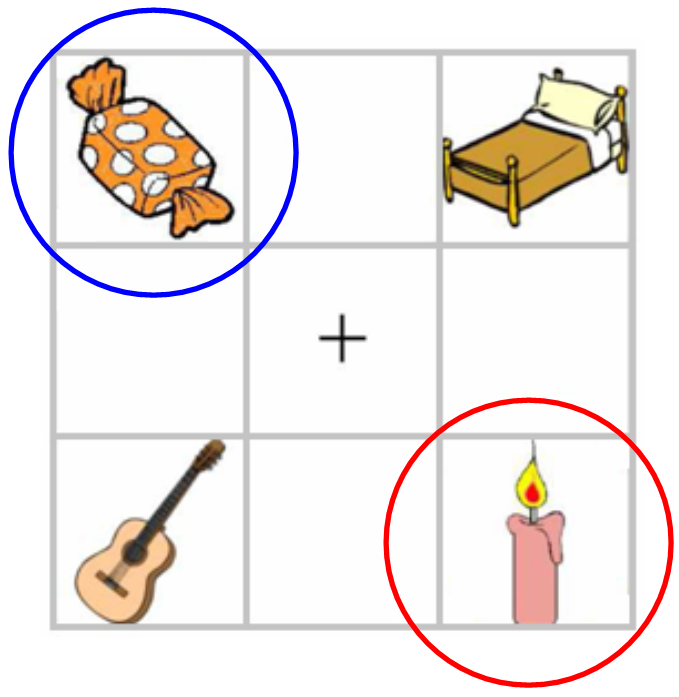
## Experimental design
* 28 Dutch participants heard sentences like:
* Klik op de rode appel ('click on the red apple')
* Klik op het plaatje met een blauw boek ('click on the image of a blue book')
* They were shown 4 nouns varying in color and gender
* Eye movements were tracked with a Tobii eye-tracker (E-Prime extensions)
---
## Experimental design: conditions
* Subjects were shown 96 different screens
* 48 screens for indefinite sentences (klik op het plaatje met een rode appel)
* 48 screens for definite sentences (klik op de rode appel)
---
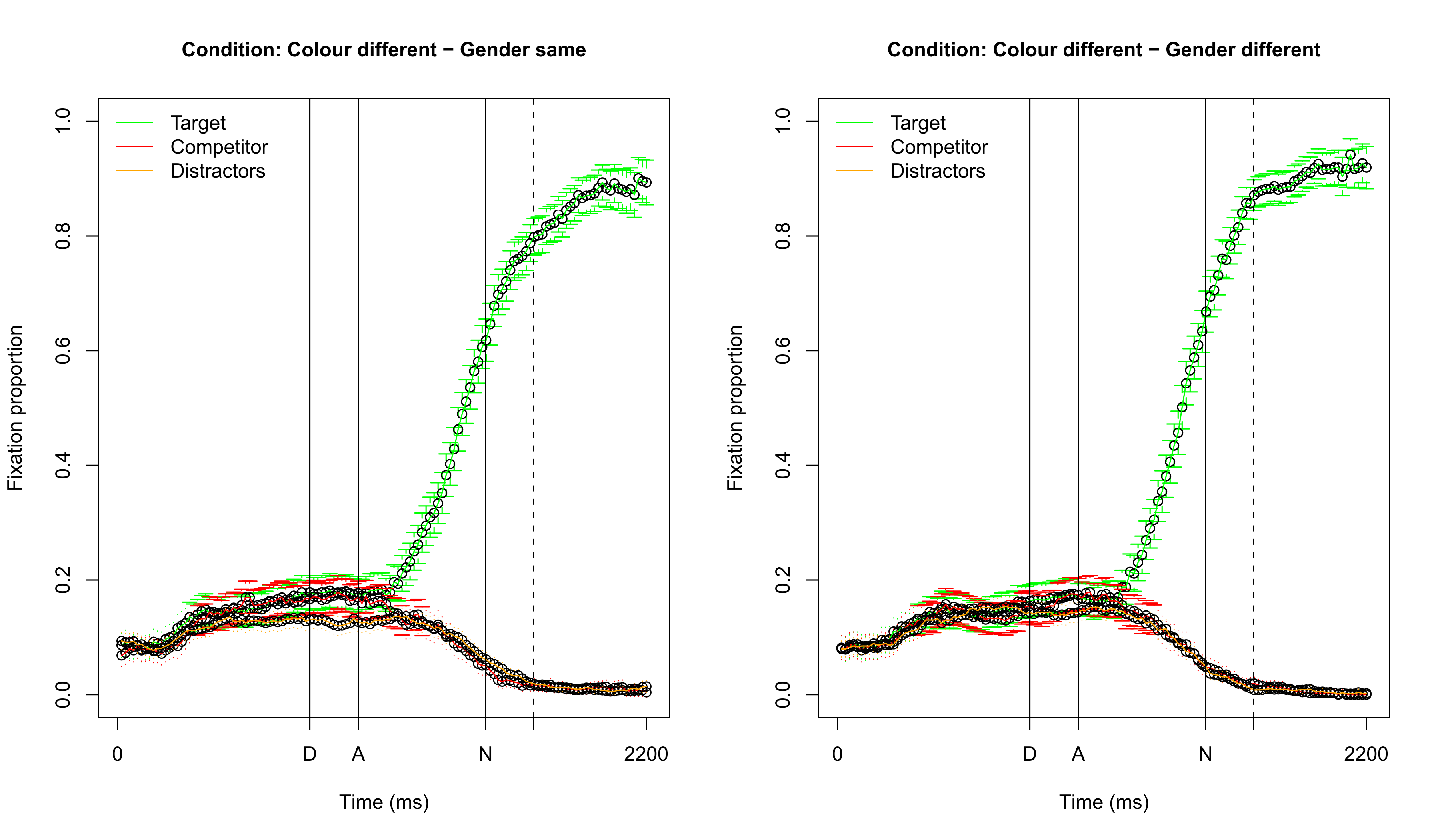
## Visualizing fixation proportions: different color
---
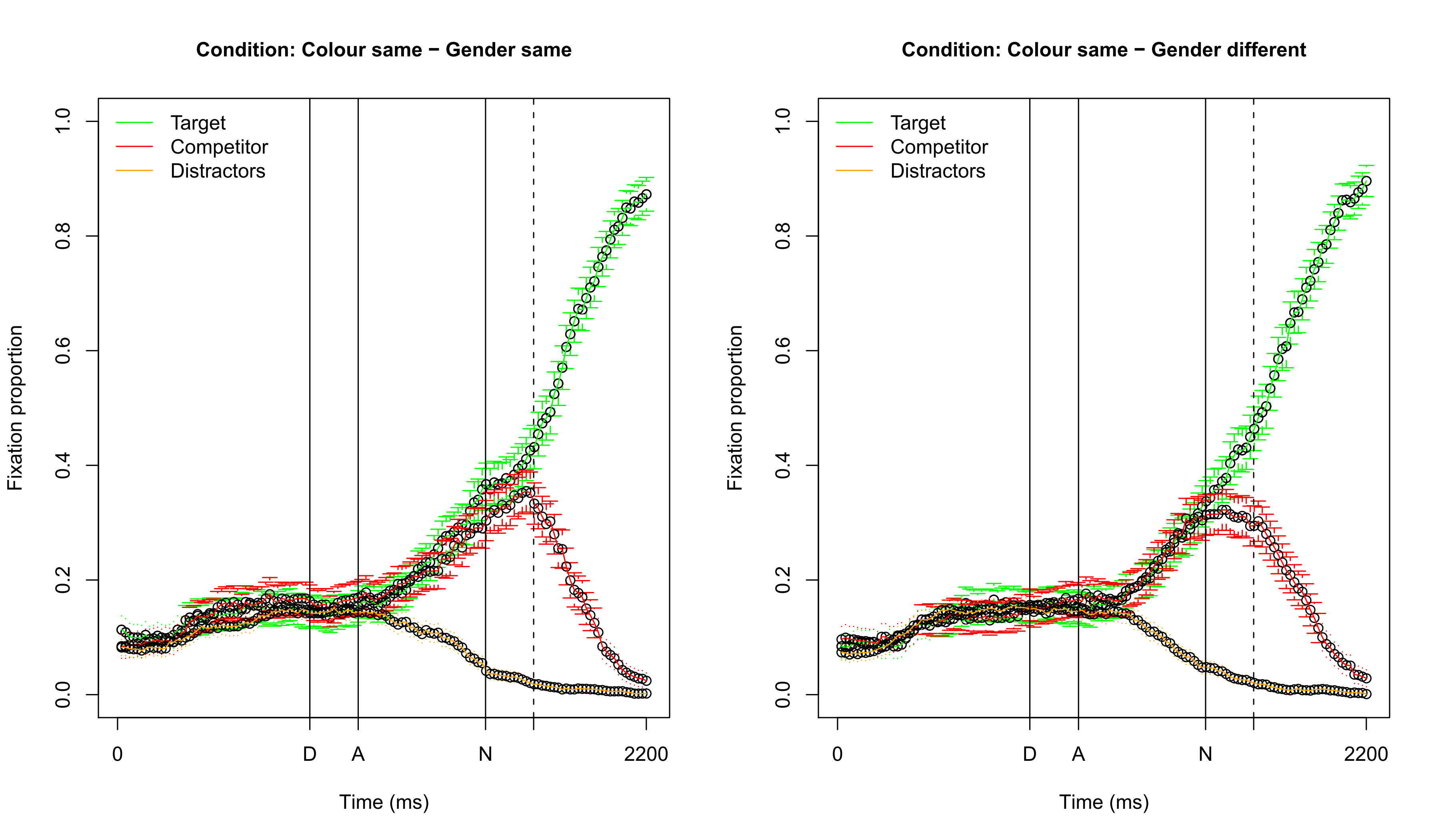
## Visualizing fixation proportions: same color
---
## Which dependent variable?
* Difficulty 1: choosing the dependent variable
* Fixation difference between Target and Competitor
* Fixation proportion on Target: requires transformation to empirical logit, to ensure the dependent variable is unbounded: $log( \frac{(y + 0.5)}{(N - y + 0.5)} )$
* ...
* Difficulty 2: selecting a time span
* Note that about 200 ms. is needed to plan and launch an eye movement
* It is possible (and better) to take every individual sampling point into account, but we will opt for the simpler approach here (in contrast to the GAM approach explained in later lectures)
* In this lecture we use:
* The difference in fixation time between Target and Competitor
* Averaged over the time span starting 200 ms. after the onset of the determiner and ending 200 ms. after the onset of the noun (about 800 ms.)
* This ensures that gender information has been heard and processed, both for the definite and indefinite sentences
---
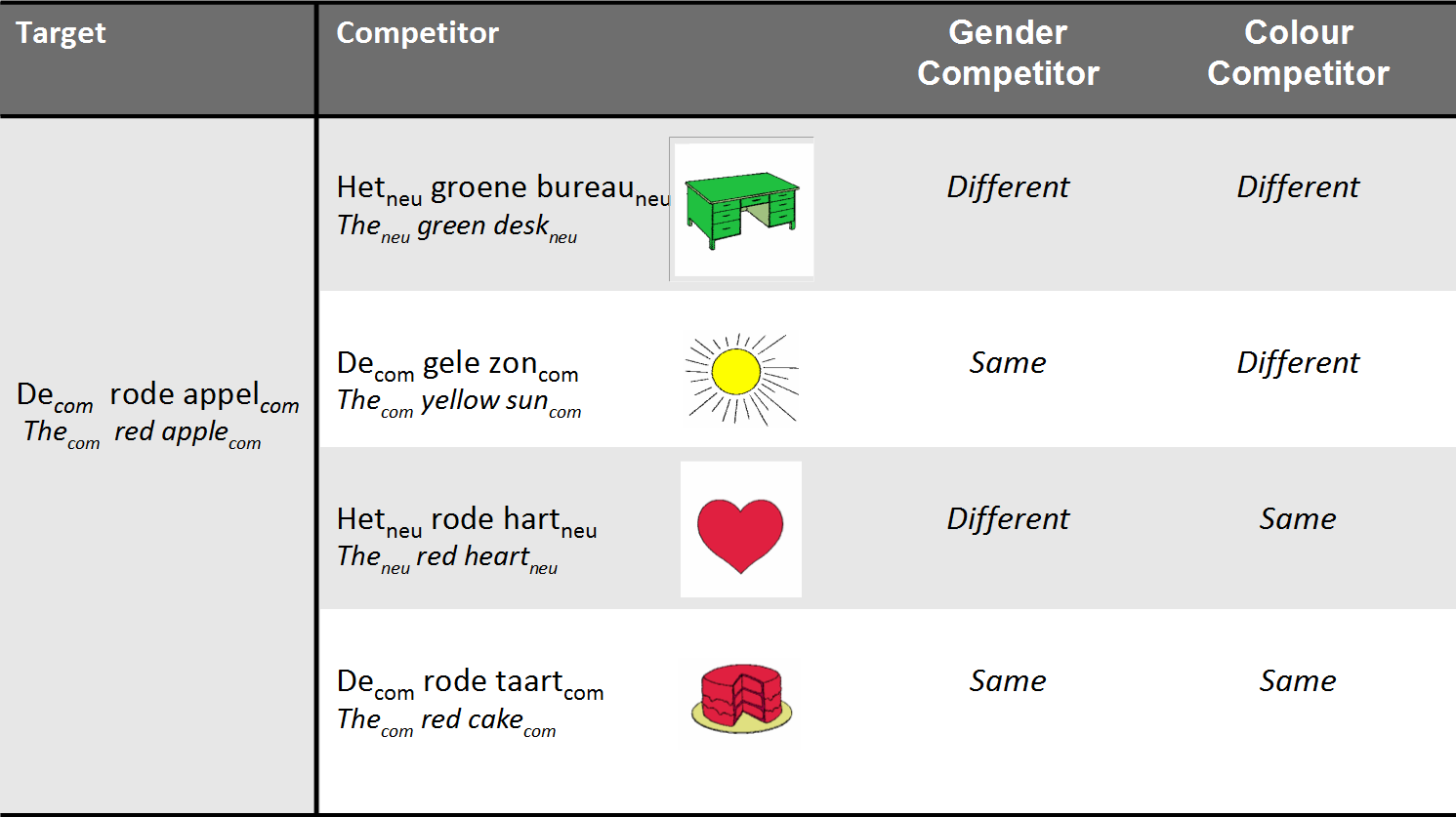
## Independent variables
* Variable of interest:
* Competitor gender vs. target gender
* Variables which could be important:
* Competitor color vs. target color
* Gender of target (common or neuter)
* Definiteness of target
* Participant-related variables:
* Gender (male/female), age, education level
* Trial number
* Design control variables:
* Competitor position vs. target position (up-down or down-up)
* Color of target
* ... (anything else you are not interested in, but potentially problematic)
---
## Some remarks about data preparation
* Check if variables correlate highly
* If so: exclude variable / combine variables (residualization is not OK: Wurm & Fisicaro, 2014)
* See Chapter 6.2.2 of Baayen (2008)
* Check if numerical variables are normally distributed
* If not: try to make them normal (e.g., logarithmic or inverse transformation)
* Note that your dependent variable does not need to be normally distributed (the residuals of your model do!)
* Center your numerical predictors when doing mixed-effects regression
* See previous lecture
---
## Our data
```r
head(eye)
```
```
# Subject Item TargetDefinite TargetNeuter TargetColor TargetPlace CompColor CompPlace TrialID
# 1 S300 boom 1 0 green 3 brown 2 1
# 2 S300 bloem 1 0 red 4 green 2 2
# 3 S300 anker 1 1 yellow 3 yellow 2 3
# 4 S300 auto 1 0 green 3 brown 2 4
# 5 S300 boek 1 1 blue 4 blue 3 5
# 6 S300 varken 1 1 brown 1 green 3 6
# Age IsMale Edulevel SameColor SameGender TargetPerc CompPerc FocusDiff
# 1 52 0 1 0 1 43.2 40.9 2.27
# 2 52 0 1 0 0 100.0 0.0 100.00
# 3 52 0 1 1 1 72.7 27.3 45.45
# 4 52 0 1 0 0 100.0 0.0 100.00
# 5 52 0 1 1 0 11.8 20.6 -8.82
# 6 52 0 1 0 0 0.0 51.2 -51.16
```
--- .smallcode
## Our first mixed-effects regression model
#### (R version 3.3.2 (2016-10-31), lme4 version 1.1.12)
```r
# A model having only random intercepts for Subject and Item
library(lme4)
model = lmer(FocusDiff ~ (1 | Subject) + (1 | Item), data = eye)
summary(model)
```
```
# Linear mixed model fit by REML ['lmerMod']
# Formula: FocusDiff ~ (1 | Subject) + (1 | Item)
# Data: eye
#
# REML criterion at convergence: 24855
#
# Scaled residuals:
# Min 1Q Median 3Q Max
# -2.897 -0.589 0.169 0.721 1.739
#
# Random effects:
# Groups Name Variance Std.Dev.
# Item (Intercept) 33.5 5.79
# Subject (Intercept) 294.3 17.16
# Residual 3294.0 57.39
# Number of obs: 2266, groups: Item, 48; Subject, 28
#
# Fixed effects:
# Estimate Std. Error t value
# (Intercept) 28.83 3.61 7.99
```
---
## By-item random intercepts
 ---
## By-subject random intercepts
---
## By-subject random intercepts
 ---
## Is a by-item analysis necessary?
```r
# comparing two models (REML=T for random effect comparison: default)
model1 = lmer(FocusDiff ~ (1 | Subject), data = eye)
model2 = lmer(FocusDiff ~ (1 | Subject) + (1 | Item), data = eye)
AIC(model1) - AIC(model2)
```
```
# [1] 1.97
```
* the AIC value is lower than 2, so we can exclude the by-item random intercept
* This indicates that the different conditions were well-controlled in the research design
---
## Adding a fixed-effect factor
```r
# model with fixed effects, but no random-effect factor for Item
model3 = lmer(FocusDiff ~ SameColor + (1 | Subject), data = eye)
summary(model3)$coef
```
```
# Estimate Std. Error t value
# (Intercept) 49.7 3.33 14.9
# SameColor -43.3 2.26 -19.2
```
*
---
## Is a by-item analysis necessary?
```r
# comparing two models (REML=T for random effect comparison: default)
model1 = lmer(FocusDiff ~ (1 | Subject), data = eye)
model2 = lmer(FocusDiff ~ (1 | Subject) + (1 | Item), data = eye)
AIC(model1) - AIC(model2)
```
```
# [1] 1.97
```
* the AIC value is lower than 2, so we can exclude the by-item random intercept
* This indicates that the different conditions were well-controlled in the research design
---
## Adding a fixed-effect factor
```r
# model with fixed effects, but no random-effect factor for Item
model3 = lmer(FocusDiff ~ SameColor + (1 | Subject), data = eye)
summary(model3)$coef
```
```
# Estimate Std. Error t value
# (Intercept) 49.7 3.33 14.9
# SameColor -43.3 2.26 -19.2
```
* SameColor is highly important as $|t| > 2$
* Negative estimate: more difficult to distinguish target from competitor
* We need to test if the effect of SameColor varies per subject
* If there is much between-subject variation, this will influence the significance of the variable in the fixed effects
---
## Testing for a random slope
```r
# as SameColor is a binary predictor (contrasting it with the intercept), it needs to be correlated
# with the random intercept
model4 = lmer(FocusDiff ~ SameColor + (1 + SameColor | Subject), data = eye)
AIC(model3) - AIC(model4)
```
```
# [1] 9.82
```
```r
summary(model4)$varcor
```
```
# Groups Name Std.Dev. Corr
# Subject (Intercept) 19.3
# SameColor 12.0 -0.86
# Residual 53.3
```
```r
summary(model4)$coef
```
```
# Estimate Std. Error t value
# (Intercept) 49.6 4.03 12.3
# SameColor -44.2 3.23 -13.7
```
* Note SameColor is still highly significant as $|t| > 2$ (absolute value)
---
## Investigating the gender effect
```r
model5 = lmer(FocusDiff ~ SameColor + SameGender + (1 + SameColor | Subject), data = eye)
summary(model5)$coef
```
```
# Estimate Std. Error t value
# (Intercept) 49.01 4.18 11.735
# SameColor -44.21 3.24 -13.657
# SameGender 1.15 2.24 0.513
```
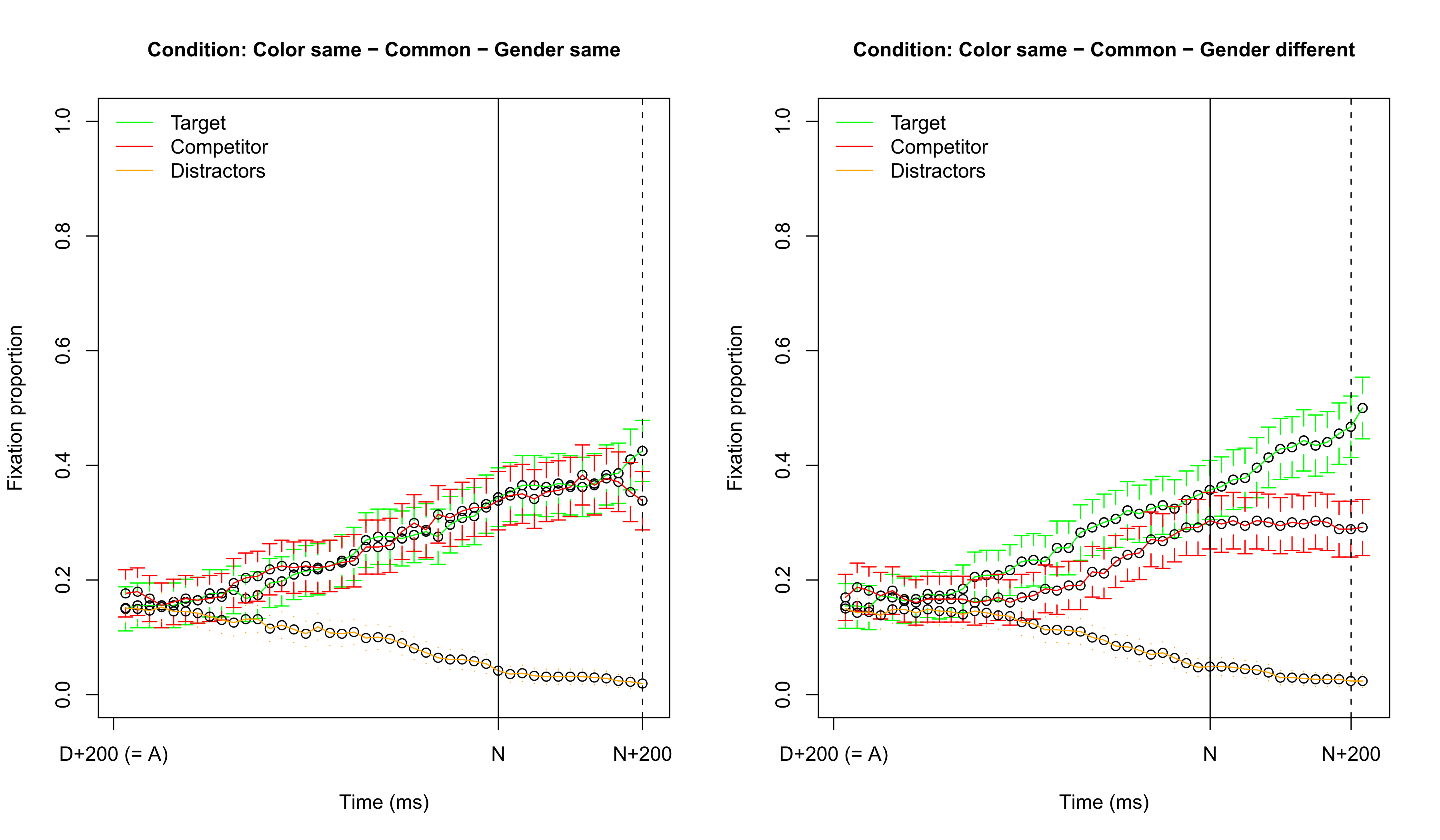
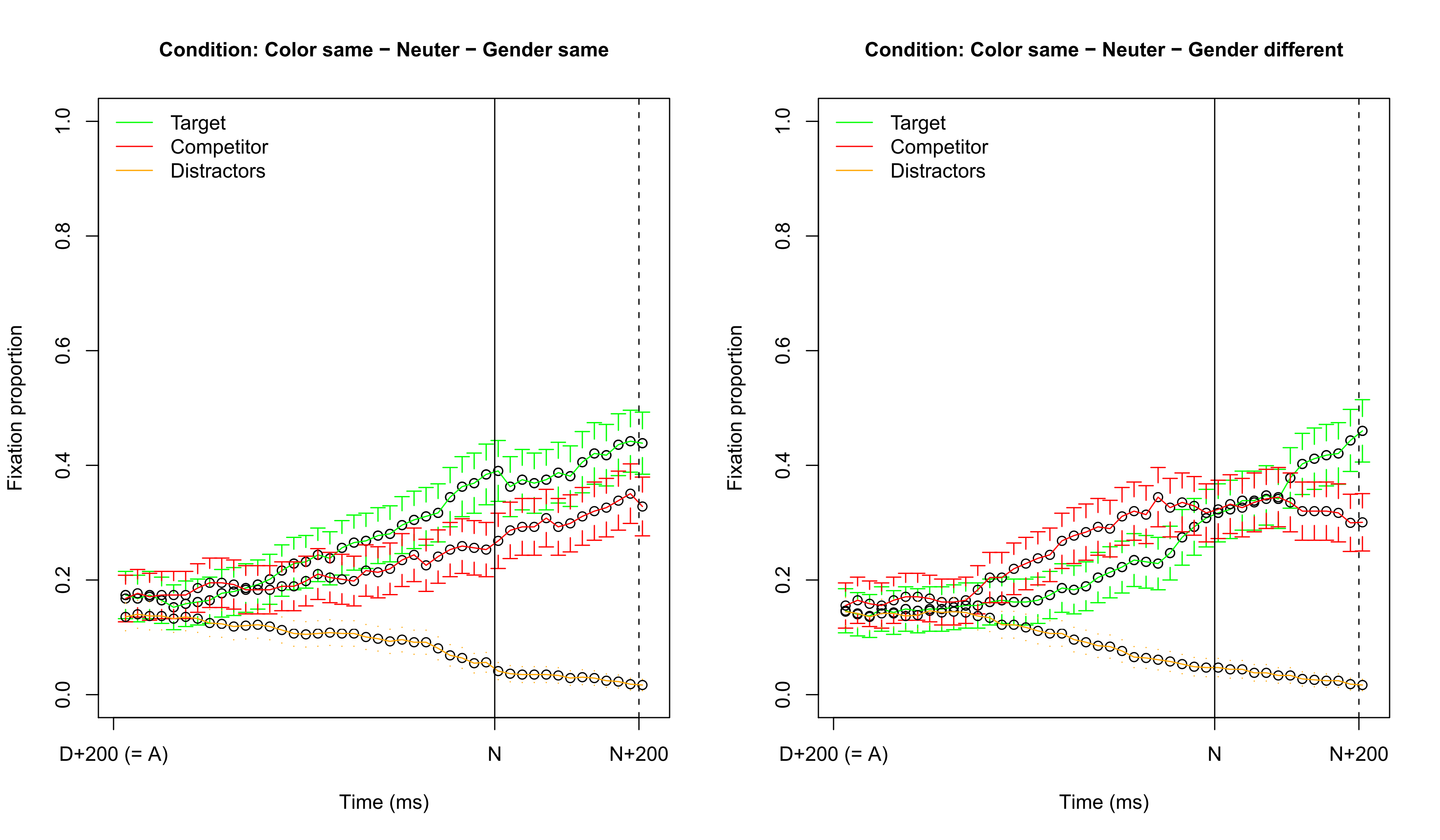
* It seems there is no gender effect...
* Perhaps there is an effect of common vs. neuter gender?
---
## Visualizing fixation proportions: target common
---
## Visualizing fixation proportions: target neuter
---
## Testing the interaction
```r
model6 = lmer(FocusDiff ~ SameColor + SameGender * TargetNeuter + (1 + SameColor | Subject), data = eye)
summary(model6)$coef
```
```
# Estimate Std. Error t value
# (Intercept) 54.34 4.47 12.16
# SameColor -44.32 3.23 -13.71
# SameGender -5.92 3.14 -1.88
# TargetNeuter -10.65 3.15 -3.38
# SameGender:TargetNeuter 14.29 4.47 3.20
```
* There is clear support for an interaction (the $|t|$'s are all close to 2)
* These results are in line with the previous fixation proportion graphs
---
## Testing if the interaction yields an improved model
```r
# To compare models differing in fixed effects, we specify REML=F. We compare to the best model we
# had before, and include TargetNeuter as it is also significant by itself.
model6a = lmer(FocusDiff ~ SameColor + SameGender + TargetNeuter + (1 + SameColor | Subject), data = eye,
REML = F)
model6b = lmer(FocusDiff ~ SameColor + SameGender * TargetNeuter + (1 + SameColor | Subject), data = eye,
REML = F)
AIC(model6a) - AIC(model6b)
```
```
# [1] 8.21
```
* The interaction improves the model significantly
* Unfortunately, we do not have an explanation for the strange neuter pattern
* Note that we still need to test the variables for inclusion as random slopes (we do this in the lab session)
---
## Adding a factor to the model
```r
# set a reference level for the factor
eye$TargetColor = relevel(eye$TargetColor, "brown")
model7 = lmer(FocusDiff ~ SameColor + SameGender * TargetNeuter + TargetColor + (1 + SameColor | Subject),
data = eye)
summary(model7)$coef
```
```
# Estimate Std. Error t value
# (Intercept) 41.36 5.10 8.12
# SameColor -44.46 3.21 -13.86
# SameGender -5.78 3.13 -1.85
# TargetNeuter -10.80 3.13 -3.45
# TargetColorblue 11.54 3.66 3.15
# TargetColorgreen 16.14 3.65 4.42
# TargetColorred 16.67 3.65 4.57
# TargetColoryellow 18.29 3.65 5.01
# SameGender:TargetNeuter 14.23 4.44 3.20
```
--- .smallcode
## Comparing different factor levels
```r
library(multcomp)
summary(glht(model7, linfct = mcp(TargetColor = "Tukey")))
```
```
#
# Simultaneous Tests for General Linear Hypotheses
#
# Multiple Comparisons of Means: Tukey Contrasts
#
#
# Fit: lmer(formula = FocusDiff ~ SameColor + SameGender * TargetNeuter +
# TargetColor + (1 + SameColor | Subject), data = eye)
#
# Linear Hypotheses:
# Estimate Std. Error z value Pr(>|z|)
# blue - brown == 0 11.545 3.660 3.15 0.014 *
# green - brown == 0 16.135 3.648 4.42 <0.001 ***
# red - brown == 0 16.673 3.646 4.57 <0.001 ***
# yellow - brown == 0 18.290 3.649 5.01 <0.001 ***
# green - blue == 0 4.591 3.447 1.33 0.671
# red - blue == 0 5.128 3.447 1.49 0.570
# yellow - blue == 0 6.745 3.448 1.96 0.288
# red - green == 0 0.537 3.433 0.16 1.000
# yellow - green == 0 2.155 3.436 0.63 0.971
# yellow - red == 0 1.617 3.435 0.47 0.990
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# (Adjusted p values reported -- single-step method)
```
---
## Simplifying the factor in a contrast
```r
eye$TargetBrown = (eye$TargetColor == "brown") * 1
model8 = lmer(FocusDiff ~ SameColor + SameGender * TargetNeuter + TargetBrown + (1 + SameColor | Subject),
data = eye)
summary(model8)$coef
```
```
# Estimate Std. Error t value
# (Intercept) 57.08 4.50 12.69
# SameColor -44.50 3.22 -13.84
# SameGender -5.81 3.13 -1.86
# TargetNeuter -10.82 3.14 -3.45
# TargetBrown -15.68 2.98 -5.26
# SameGender:TargetNeuter 14.26 4.44 3.21
```
```r
# model7b and model8b: REML=F instead of the default (TRUE)
AIC(model8b) - AIC(model7b) # N.B. model7b is more complex
```
```
# [1] -1.77
```
---
## How well does the model fit?
```r
cor(eye$FocusDiff, fitted(model8))^2 # 'explained variance' of the model (r-squared)
```
```
# [1] 0.23
```
```r
qqnorm(resid(model8))
qqline(resid(model8))
```
 ---
## Model criticism
```r
eye2 = eye[abs(scale(resid(model8))) < 2.5, ] # remove items with which the model has trouble fitting
1 - (nrow(eye2)/nrow(eye)) # only about 0.35% removed
```
```
# [1] 0.00353
```
```r
model9 = lmer(FocusDiff ~ SameColor + SameGender * TargetNeuter + TargetBrown + (1 + SameColor | Subject),
data = eye2)
cor(eye2$FocusDiff, fitted(model9))^2 # improved explained variance
```
```
# [1] 0.243
```
```r
summary(model9)$coef # all variables significant
```
```
# Estimate Std. Error t value
# (Intercept) 58.09 4.55 12.76
# SameColor -45.56 3.34 -13.64
# SameGender -6.32 3.09 -2.05
# TargetNeuter -10.52 3.10 -3.39
# TargetBrown -15.79 2.95 -5.36
# SameGender:TargetNeuter 14.82 4.39 3.37
```
---
## Many more things to do...
* We need to see if the significant fixed effects remain significant when adding these variables as random slopes per subject
* There are other variables we should test (e.g., education level)
* There are other interactions we can test
* Model criticism should be applied after these steps
* We will experiment with these issues in the lab session after the break!
* We use a subset of the data (only same color)
* Simple
---
## Model criticism
```r
eye2 = eye[abs(scale(resid(model8))) < 2.5, ] # remove items with which the model has trouble fitting
1 - (nrow(eye2)/nrow(eye)) # only about 0.35% removed
```
```
# [1] 0.00353
```
```r
model9 = lmer(FocusDiff ~ SameColor + SameGender * TargetNeuter + TargetBrown + (1 + SameColor | Subject),
data = eye2)
cor(eye2$FocusDiff, fitted(model9))^2 # improved explained variance
```
```
# [1] 0.243
```
```r
summary(model9)$coef # all variables significant
```
```
# Estimate Std. Error t value
# (Intercept) 58.09 4.55 12.76
# SameColor -45.56 3.34 -13.64
# SameGender -6.32 3.09 -2.05
# TargetNeuter -10.52 3.10 -3.39
# TargetBrown -15.79 2.95 -5.36
# SameGender:TargetNeuter 14.82 4.39 3.37
```
---
## Many more things to do...
* We need to see if the significant fixed effects remain significant when adding these variables as random slopes per subject
* There are other variables we should test (e.g., education level)
* There are other interactions we can test
* Model criticism should be applied after these steps
* We will experiment with these issues in the lab session after the break!
* We use a subset of the data (only same color)
* Simple R-functions are used to generate all plots
---
## Recap
* We have learned that mixed-effects regression models:
* offer an easy-to-use approach to obtain generalizable results even when your design is not completely balanced
* allow a fine-grained inspection of the variability of the random effects, which may provide additional insight in your data
* are easy to construct in R!
* Note that we analyzed this data in a non-optimal way: rather than averaging over a timespan, it is better to predict the focus for every individual timepoint using generalized additive modeling (the following lectures will illustrate this)
* After the break:
* http://www.let.rug.nl/wieling/statscourse/lecture2/lab
* Next lecture: introduction to generalized additive modeling
--- {
tpl: thankyou,
social: [{title: www, href: "http://www.martijnwieling.nl"}, {title: eml, href: "wieling@gmail.com"}]
}
## Questions?
Thank you for your attention!