Databestanden:
/net/aistaff/vannoord/z/Alpino/Treelets/CFG
/net/aistaff/vannoord/z/Alpino/Suites/Machine
Programma's:
/net/aistaff/kleiweg/Earley
Verwerkingstijden voor het parsen (dus exclusief inlezen gegevens) voor standaardzin:
clef, 1 deel |
0,6s |
clef, 30 delen |
10,2s |
Aantallen unieke termen en regels:
clef, rules, 30 delen |
773652 |
clef, terms, 30 delen |
549702 |
clef, rules, 1 deel |
64344 |
clef, terms, 1 deel |
44919 |
Percentages van verwerkte zinnen (één clef-deel, getest op aantal andere delen):
|
zonder gokken |
met gokken |
|||
delen |
onbekend |
fail |
OK |
fail |
OK |
1 |
80.4% |
14.1% |
5.5% |
39.6% |
60.4% |
2 |
72.2% |
17.7% |
10.1% |
||
3 |
66.9% |
17.7% |
15.4% |
||
4 |
62.7% |
18.4% |
18.9% |
28.5% |
71.5% |
5 |
60.1% |
18.2% |
21.7% |
||
6 |
57.3% |
18.5% |
24.2% |
||
7 |
55.4% |
18.1% |
26.5% |
||
9 |
51.9% |
17.5% |
30.6% |
21.0% |
79.0% |
12 |
47.6% |
17.0% |
35.4% |
||
14 |
45.6% |
16.5% |
37.9% |
||
17 |
43.4% |
16.0% |
40.6% |
||
19 |
41.9% |
15.7% |
42.4% |
||
22 |
40.3% |
14.8% |
44.9% |
||
24 |
39.7% |
14.3% |
46.0% |
||
27 |
38.6% |
13.0% |
48.4% |
||
28 |
38.2% |
13.2% |
48.6% |
||
aantal testzinnen: 1000
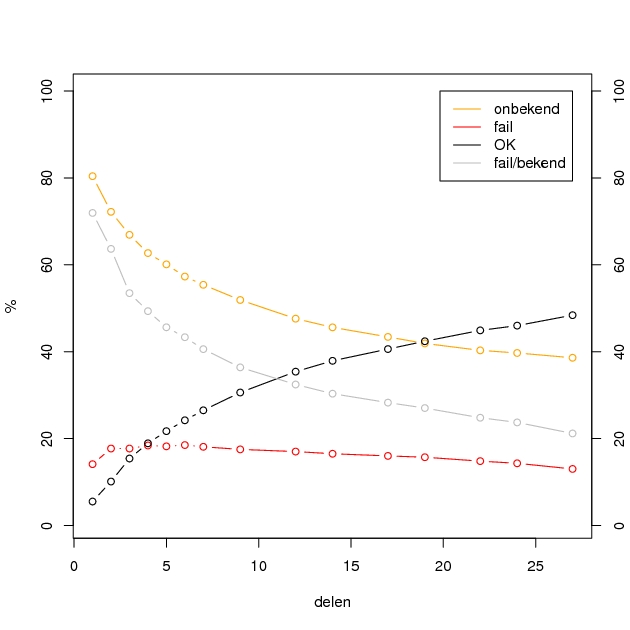
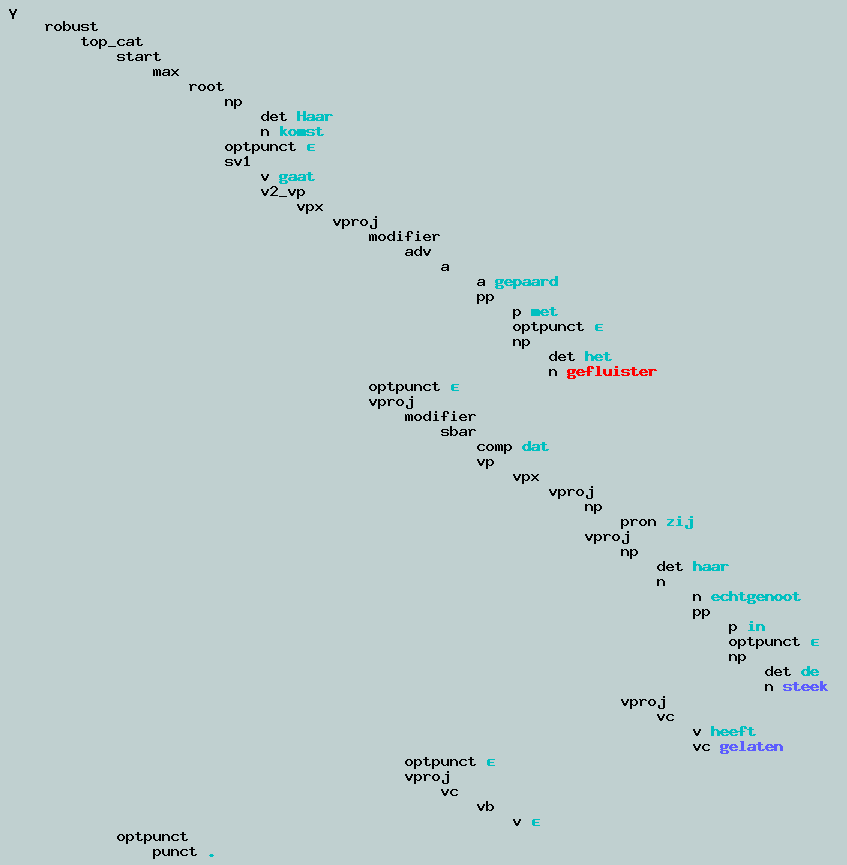
Gokken: rood = onbekend woord, blauw = woord met category waarmee het niet in de tabel past.
Eerste: kleine grammatica, onjuiste parse.
Tweede: grote grammatica, minder onjuiste parse.
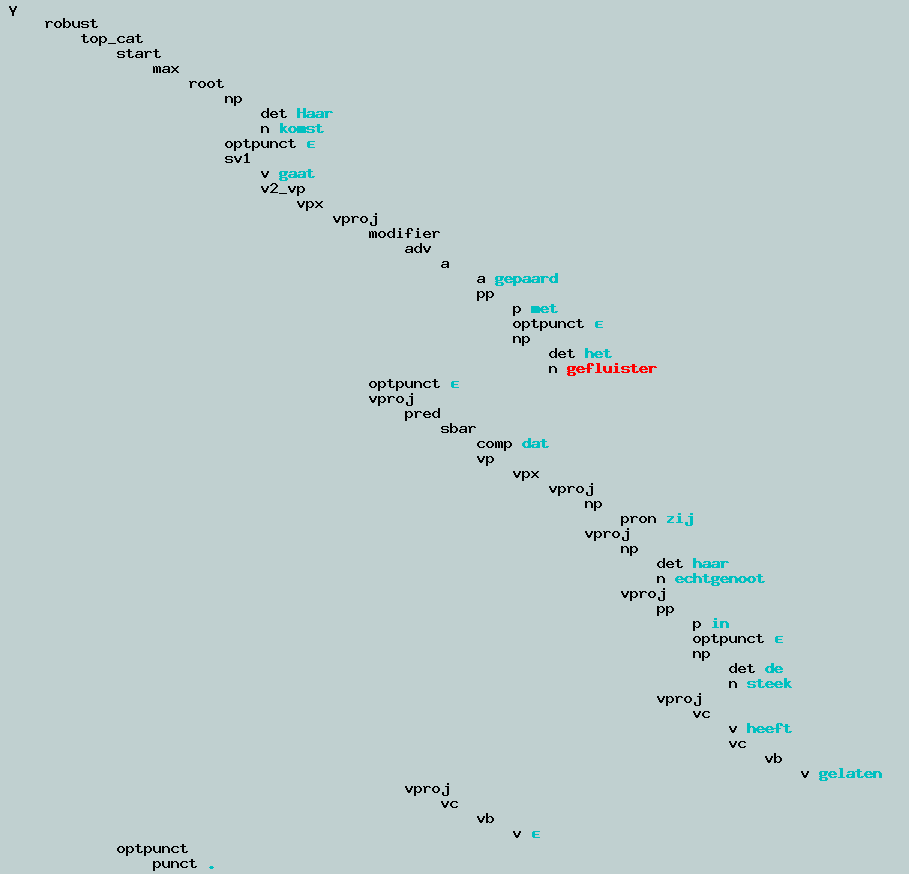
Derde: grote grammatica, alleen bekende woorden, juiste parse?

Voorbeelden van zinnen die grammatica van alleen het eerste deel van clef niet vindt, al zijn alle woorden aanwezig in het lexicon:
- Er zijn zeehonden gezien in het Noordzeegebied .
- Hij geeft haar een fiets .
- Hij rijdt op de fiets .
Betekent dit dat de regels veel te specifiek zijn?
Al deze zinnen worden wel herkend met de grammatica van 30 delen van clef.
Werken met waarschijnlijkheden vraagt een bepaalde structuur in de grammatica. Bijvoorbeeld, met deze regels...
S → NP VP
NP → N
NP → Det Adjs N PP
Adjs → Adj Adjs
Adjs →
VP → V NP PP
PP → P NP
PP →... is er geen verschil tussen de waarschijnlijkheid dat de PP leeg is tussen de NP-regel en de VP-regel. Op dit niveau ligt de keus vast. Houdt dat in dat je geen lege categorieën kunt gebruiken?
Vergelijk hiermee:
S → NP VP
NP → N
NP → Det N
NP → Det N PP
NP → Det Adjs N
NP → Det Adjs N PP
Adjs → Adj
Adjs → Adj Adjs
VP → V NP
VP → V NP PP
PP → P NPHier wordt de keus van de PP-attachment bepaald door de waarschijnlijkheden van de NP-regels en de VP-regels.
Maar waarschijnlijkheid wordt ook bepaald door omvang van de subboom die onder elke rhs van een regel zit. Hoe groter die subboom, hoe onwaarschijnlijker de regel als geheel wordt.
Dit lijkt niet te kloppen. Taalgebruik is vaak redundant. Mensen gebruiken meer woorden dan strikt noodzakelijk. Maar als je waarschijnlijkheden gaat vermenigvuldigen worden zinnen met redundantie al onwaarschijnlijker dan zinnen zonder redundantie met dezelfde betekenis. Het is juist toevoeging van nieuwe informatie die een zin onwaarschijnlijker maakt: witte sneeuw is waarschijnlijker dan groene sneeuw.
In een "natuurlijk" lexicon hebben woorden informatie over met welke andere woorden ze willen voorkomen, en in welke verbanden. Is dit (effectief) te vangen in een grammatica voor een top-down parser? Vergelijk:
Hij gaat
op de fiets
naar Groningen
Hij neemt
de bus
naar Groningen
Hij stuurt
de bus
naar Groningen
Hij ziet
de man
met de verrekijker
Hij ontmoet
de man
met de verrekijker
Dat is iets voor morgen.
Het moet voor morgen af zijn.
Ik heb genoeg tot morgen.
Tot morgen!
Er is voor elke prijs wat te vinden.
We doen het tot elke prijs.
Dit vraagt om Construction Grammar. (Of Word Grammar misschien?)
