Next: Top-down generators and Up: An Overview of Head Previous: Introduction
Problems with early approaches
This section gives an overview of some of the problems that led to the head driven bottom-up approach.
Problems that a generator can face are divided in two types.
The first type of problem is the following.
It is quite easy to define grammar rules which most known generators will fail
to handle (eg. a rule such as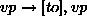 
).
In fact, the generation problem in (unrestricted)
unification grammars can easily be proved to be undecidable. Therefore each generator
is usually restricted to a particular class of grammars for which it is useful, although
this class is not always clearly defined. I am interested in a generator that
will work for linguistically relevant unification grammars, thus I
prefer some generator over another if it handles some linguistically
motivated grammar whereas the other does not.
It is clear that people may disagree on the notion `linguistically relevant'. Consequently implementations of different linguistic theories may use different generation algorithms. In this paper I am interested in the family of lexical and sign-based linguistic theories, for example theories such as HPSG [18], and unification-based versions of categorial grammar [28][32].
The second type of problem is simply the performance of the generator. Although it is hard to give any complexity results for generation from a unification grammar (for example because the problem is undecidable), it seems to be possible to prefer generators that are more goal-directed than others - resulting in dramatical differences in performance.
First I will describe the principal problem for top-down generators such as the LFG-generator of Wedekind [31] and the generator for 's of Dymetman and Isabelle [7]. Then I will discuss the chart-based bottom up generator of Shieber [21].
Gertjan van Noord
Fri Nov 25 13:07:08 MET 1994