Reversibility

Intuitively, we call a program `reversible' if it is capable of both parsing and generation on the basis of a single characterization of the relation between semantic structures and phonological structures. The following definitions of reversibility are meant to be independent of the way we go about achieving a reversible natural language processing component. Furthermore, the definitions abstract away from the actual representations between which we are defining relations.

A program or system will be called r-reversible iff it computes a binary relation r in both directions. The idea is that, given an element of a pair in the relation, the program computes the corresponding element(s) of that pair. To encode the `direction' of the relation I assume that the input for the program consists of a pair $\langle$dir, x$\rangle$ where dir represents the direction which the program should compute. The value of dir is either 0 or 1. If the value is 0, then the program computes the relation from left to right; if the value is 1 then the program computes the relation from right to left. ³

Definition 1 (Compute a relation in both directions)   A program P computes a relation r in both directions, iff P enumerates for a given input $\langle$dir, e$\rangle$ the set

{x|$$\begin{array}{l} \langle e,x \rangle \in r \wedge dir=0 ~\vee \\ \langle x,e \rangle \in r \wedge dir=1 \end{array}$$}

Definition 2 (Reversible)  

• A program P is r-reversible iff P computes r in both directions.
• A relation r is reversible iff there exists an r-reversible program.

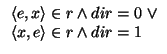Consider the case where r is the relation between phonological and semantic representations defined by some grammar. In this case a program is said to compute this relation in both directions (i.e. the program is reversible w.r.t. this relation) iff for a given phonological representation the program returns the corresponding semantic representation; for a given semantic representation the program returns the corresponding phonological representations. Such a program may consist of a parser and a generator (depending on the value of dir), or alternatively the program consists of a single uniform algorithm.

Systems in which the relation between phonological and semantic representations is defined procedurally are seldom reversible in this respect, because it is very difficult to make sure that the program indeed computes the same relation in both directions. On the other hand, a system based on a single declarative grammar necessarily is reversible.

Arguably, the above defined notion of reversibility is somewhat weak. According to the definition above, any recursively enumerable relation is reversible. However, in practice it is often the case that a grammar that is developed from a single perspective (eg. parsing perspective) is completely useless in the other direction because it simply fails to terminate in all interesting cases (let alone efficiency considerations). Therefore, we define what it means for a relation to be effectively reversible. A relation is effectively reversible if it can be effectively computed in both directions, i.e. there exists a program computing the relation in both directions, and furthermore the program always halts. In the terminology of [Hopcroft and Ullman1979], we require that there exists an algorithm computing the relation.

Definition 3 (Effectively reversible)  

• A program P is effectively r-reversible iff
  • P is r-reversible; and
  • P is guaranteed to terminate (for every input).
• A relation r is effectively reversible iff there exists an effectively r-reversible program.

If we use the term reversible in the remainder of this article, then we will invariably mean effectively reversible.