---

Next: Recursive Constraints Up: Constraint-Based Categorial Grammar Previous: Constraint-Based Categorial Grammar

---

Introduction

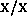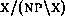Combinations of Categorial Grammar (CG) and unification naturally lead to the introduction of polymorphic categories. Thus, Karttunen [11] categorizes NP's as , where X is a verbal category, Zeevat et al. [17] assign the category to NP's, and Emms [6] extends the Lambek-calculus with polymorphic categories to account for coordination, quantifier scope, and extraction.

The role of polymorphism has been restricted, however, by the fact that in previous work categories were defined as feature structures using the simple, non-recursive, constraints familiar from feature description languages such as PATR. Relational constraints can be used to define a range of polymorphic categories that are beyond the expressive capabilities of previous approaches.

In particular, the introduction of relational constraints captures the effects of (recursive) lexical rules in a computationally attractive manner. The addition of such rules makes it feasible to consider truly `lexicalist' grammars, in which a powerful lexical component is accompanied by a highly restricted syntactic component, consisting of application only.

---

Gertjan van Noord
Fri Nov 25 16:22:41 MET 1994