

Next: acknowledgments
Up: Treatment of Epsilon Moves
Previous: Experiment: Automata generated by
We have discussed a number of variants of the subset-construction algorithm
for determinising finite automata containing 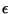 -moves.
The experiments support the following conclusions:
-moves.
The experiments support the following conclusions:
- The integrated variants per subset and per state
work much better for automata containing a large number of
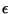 -moves. The per subset variant tends to improve
upon the per state algorithm if the number of
-moves. The per subset variant tends to improve
upon the per state algorithm if the number of
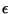 -moves increases even further.
-moves increases even further.
- We have identified four different variants of the
per graph algorithm. In our experiments, the per grapht
is the algorithm of choice for automata containing few
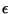 moves, because it is faster than the other algorithms, and because
it produces smaller automata than the per graphs and
per graphs,a variants.
moves, because it is faster than the other algorithms, and because
it produces smaller automata than the per graphs and
per graphs,a variants.
- The per grapht,c variant is an interesting alternative
in that it produces the smallest results. This variant should be
used if the input automaton is expected to contain many
non-co-accessible states.
- Automata produced by finite-state approximation techniques tend
to contain many
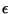 -moves. We found that for these automata
the differences in speed between the various algorithms can be
enormous. The per subset and per state algorithms
are good candidates for this application.
-moves. We found that for these automata
the differences in speed between the various algorithms can be
enormous. The per subset and per state algorithms
are good candidates for this application.
We have attempted to characterize the expected efficiency of the
various algorithms in terms of the number of jumps and the number of
states in the input automaton. It is quite conceivable that other
simple properties of the input automaton can be used even more
effectively for this purpose. One reviewer suggests to use the number
of strongly 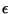 -connected components (the strongly connected
components of the graph of all
-connected components (the strongly connected
components of the graph of all 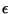 -moves) for this purpose. We
leave this and other possibilities to a future occasion.
-moves) for this purpose. We
leave this and other possibilities to a future occasion.


Next: acknowledgments
Up: Treatment of Epsilon Moves
Previous: Experiment: Automata generated by
2000-07-10
![]() -connected components (the strongly connected
components of the graph of all
-connected components (the strongly connected
components of the graph of all ![]() -moves) for this purpose. We
leave this and other possibilities to a future occasion.
-moves) for this purpose. We
leave this and other possibilities to a future occasion.