Next: Acknowledgements Up: Reversible Unification Based Machine Previous: Reentrancies
Final remarks
The objective to build a reversible MT system using a series of unification grammars is similar to the objective of the CRITTER system as expressed in [7][3], and the work of Zajac in [25]. Instead of using unification grammars CRITTER uses logic grammars; Zajac uses a type system including an inheritance mechanism to define transfer-like rules. In these two approaches less attention is being paid to an exact definition of reversibility; although our work may be compatible with these approaches.
A somewhat different approach is advocated in [9]. In that
approach a system is described where an LFG grammar for some source language
is augmented with equations that define (part of) the target level
representations. A generator derives from
this partial description a string according to some LFG grammar of the
target language. Instead of a series of three grammars this architecture
thus assumes two grammars, one of which both defines the source language and
the relation with the target language.
The translation relation is not only defined between logical forms but
may relate all levels of representation (
c-structure, f-structure, 
-structure).
Although in this approach monolingual grammars may be used in a bidirectional
way it is unclear whether the translation equations can be used
bidirectionally 
.
An important problem for the approach advocated here is the problem of logical
form equivalence. Shieber [16] noted that unification grammars usually define a
relation between strings and some canonical logical form. Depending on
the nature of logical forms that are being used, several representations
of a logical form may have the same `meaning'; just as in first order predicate
calculus the formulas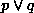 
and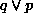 
are logically equivalent; a
unification grammar will not know of these equivalences and, consequently, all
equivalences have to be defined separately (if such equivalents are thought
of as being translational equivalents); for example in a transfer grammar
two rules may be defined to translate 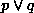into both 
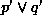and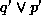 
if these formulas are thought of as being equivalent. Of course this technique can
only be applied if the number of equivalences is finite. It is not possible to
define that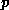 
is equivalent with 
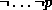for any even number of 
's.
The approach discussed so far can be extended just as unification grammars for parsing and generation have been extended. Apart from equational constraints it will be useful to add others such as disjunction and negation. Moreover it seems useful to allow some version of universal constraints or some inheritance mechanism to be able to express generalizations and exceptions more easily.
Next: Acknowledgements Up: Reversible Unification Based Machine Previous: Reentrancies
Gertjan van Noord
Fri Nov 25 13:42:02 MET 1994