Next: Reentrancies Up: Possible relaxations Previous: Possible relaxations
Cyclic and non-cyclic attributes
The first relaxation assumes that there is a sort system
defined for feature structures that makes it possible to make a distinction between
cyclic and non-cyclic attributes (cf. [5]). For the moment a non-cyclic
attribute may be defined as an attribute with a finite number of possible values (i.e.
it is not recursive). For example the attributes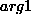 
and 
will be
cyclic whereas 
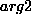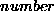will be non-cyclic. The completeness and coherence
condition is restricted to cyclic attributes. As the proof procedure can only
further instantiate non-cyclic attributes no termination problems occur because
there are only a finite number of possibilities to do this.
The definition of `equivalence' for feature structures is now slightly changed. To
define this properly it is necessary to define the notion non-cyclic
extension. A non-cyclic extension of a feature structure only instantiates
non-cyclic attributes. This results in the following definition of equivalence:
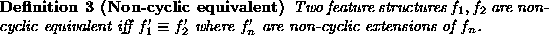
It will be clear that the usefulness of this definition depends heavily on
the style of grammar writing that is used. Note that it is of course also
possible to declare for each non-cyclic attribute whether the completeness and
coherence requirements hold.
Gertjan van Noord
Fri Nov 25 13:42:02 MET 1994