... transducer.¹

The syntax at this point is merely suggestive. As an example, suppose that T_acr transduces phrases into acronyms. Then 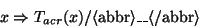$$x\Rightarrow T_{acr}(x)/\langle \mbox{abbr}\rangle\mbox{\_\_}\langle /\mbox{abbr}\rangle$$ would transduce <abbr>non-deterministic finite automaton</abbr> into <abbr>NDFA</abbr>.

To compare this with a backreference in Perl, suppose that T_acr is a subroutine that converts phrases into acronyms and that R_acr is a regular expression matching phrases that can be converted into acronyms. Then (ignoring the left context) one can write something like: s/(R_acr)(?=$\langle$/ABBR$\rangle$)/T_acr($1)/ge;. The backreference variable, $1, will be set to whatever string R_acr matches.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... not.²

This approach is similar to the idea of laying down tracks as in the compilation of monadic second-order logic into automata Klarlund (1997, p. 5). In fact, this technique could possibly be used for a more efficient implementation of our algorithm: instead of adding transitions over 0 and 1, one could represent the alphabet as bit sequences and then add a final 0 bit for any ordinary symbol and a final 1 bit for a marker symbol.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... transitions.³

The alternative implementation is provided in [17].

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... as:⁴

The line with $$(rb1) can be optimized a bit: Since we know that an rb1 must be preceded by Phi, we can write: [ign_(non_markers(Phi),brack),rb1,xsig*]). This may lead to a more constrained (hence smaller) transducer.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... top#o#logical.⁵

An anonymous reviewer suggested that lm_concat could be implemented in the framework of [8] as:

$$\mbox{[t o $\mid$ t o p $\mid$\space o $\mid$\space p o l o ] $\rightarrow$\space ... \char93 }$$;

Indeed the resulting transducer from this expression would transduce topological into top#o#logical. But unfortunately this transducer would also transduce polotopogical into polo#top#o#gical, since the notion of left-right ordering is lost in this expression.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... filtering.⁶

The bracketing operator of [8], on the other hand, does not provide for left and right contexts.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...$\mbox{\it xy} \Rightarrow [_{NP}\, \mbox{\it RepairDet(x) RepairN(y)}\,]/\lambda \mbox{\_\_}\rho$⁷

The syntax here has been simplified. The rule should be understood as: replace(lm_concat([[]:'[np', repair_det, repair_n, []:']'],lambda, rho).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.