

Next: Unification Linguistics Up: Introduction Previous: Transfer model
Computation
Monolingual and bilingual knowledge is represented in a declarative way. Declarativity implies that the grammar writer does not have to worry about the actual processing of the linguistic knowledge he/she encodes, but only worries about the logical meaning of a grammar. Declarativeness has been argued for from a computational point of view because it implies that different compilers and interpreters may be applicable to the very same program. This has led to the bidirectional use of programs written in declarative grammar formalisms such as PATR and DCG [35][27][37]. Some recent developments are reported in [40][43][39][38][8][42][36][46][10].
We make a distinction between symmetric and reversible. We
call a translation relation 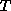 reversible if
reversible if 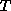 is symmetric and
computable. Symmetry of the `possible translation' relation has been argued for above.
Reversible systems are preferable to nonreversible ones. The arguments
in favour of using bidirectional grammars in NLP, such as those
given in [17][2] carry over to translation.
Furthermore Isabelle [16] claims
that reversible MT systems are to be preferred to others because
in reversible MT systems a better understanding of the translation
relation is achieved; such systems will eventually exhibit better
practical performance. Monolingual grammars that are
used only for analysis will often allow constructions that are in fact ungrammatical.
As an example consider English auxiliaries. Suppose that the English
auxiliaries are
analyzed as verbs that take an obligatory
is symmetric and
computable. Symmetry of the `possible translation' relation has been argued for above.
Reversible systems are preferable to nonreversible ones. The arguments
in favour of using bidirectional grammars in NLP, such as those
given in [17][2] carry over to translation.
Furthermore Isabelle [16] claims
that reversible MT systems are to be preferred to others because
in reversible MT systems a better understanding of the translation
relation is achieved; such systems will eventually exhibit better
practical performance. Monolingual grammars that are
used only for analysis will often allow constructions that are in fact ungrammatical.
As an example consider English auxiliaries. Suppose that the English
auxiliaries are
analyzed as verbs that take an obligatory 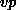 -complement. Moreover each auxiliary
may restrict the
-complement. Moreover each auxiliary
may restrict the 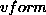 (participle, infinite) of this complement. This allows
the analysis of sentences such as `John will have been kissing mary'. However,
the possible order of English auxiliaries (eg. `have' should precede `be')
is not accounted for and the
analysis sketched above will for example allow sentences such as
`John will be having kissed Mary'.
The strictness coming with a bidirectional grammar will be useful for
analysis too, because strictness usually implies less local and
global ambiguities.
(participle, infinite) of this complement. This allows
the analysis of sentences such as `John will have been kissing mary'. However,
the possible order of English auxiliaries (eg. `have' should precede `be')
is not accounted for and the
analysis sketched above will for example allow sentences such as
`John will be having kissed Mary'.
The strictness coming with a bidirectional grammar will be useful for
analysis too, because strictness usually implies less local and
global ambiguities.


Next: Unification Linguistics Up: Introduction Previous: Transfer model
Gertjan van Noord
Thu Nov 24 18:57:05 MET 1994