


Next: Postponing Lexical Choice Up: Extensions Previous: Completeness and Coherence
Quantifier Storage
We will outline here how to generate from a quantified logical form sentences with quantified NPs one of whose readings is the original logical form, thus performing quantifier lowering automatically. For this, we will associate a quantifier store to certain categories and add to the grammar suitable store manipulation rules.
Each category whose constituents may create store elements will have a store feature. Furthermore, for each such category whose semantics can be the scope of a quantifier, there will be an optional non-chain rule to take the top element of an ordered store and apply it to the semantics of the category. For example, here is the rule for sentences:
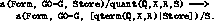
The term quant(Q,X,R,S) represents a quantified formula with quantifier Q, bound variable X, restriction R and scope S, and qterm(Q,X,R) is the corresponding store element.
In addition, some mechanism is needed to combine the stores of the immediate constituents of a phrase into a store for the phrase. For example, the combination of subject and complement stores for a verb into a clause store is done in one of our test grammars by lexical rules such as
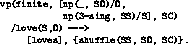
which states that the store SC of a clause with main verb
`love' and the stores SS and SO of the subject and
object the verb subcategorizes for satisfy the constraint
shuffle(SS, SO, SC), meaning that SC is an interleaving of
elements of SS and SO in their original order.

Finally, it is necessary to deal with the noun phrases that create store elements. Ignoring the issue of how to treat quantifiers from within complex noun phrases, we just need lexical rules for determiners, of the form
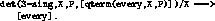
stating that the semantics of a quantified NP is simply the variable bound by the store element arising from the NP. For rules of this form to work properly, it is essential that distinct bound logical-form variables be represented as distinct constants in the terms encoding the logical forms. This is an instance of the problem of coherence discussed in the previous section.
The rules outlined here are less efficient than necessary because the distribution of store elements among the subject and complements of a verb does not check whether the variable bound by a store element actually appears in the semantics of the phrase to which it is being assigned, leading to many dead ends in the generation process. Also, the rules are sound for generation but not for analysis, because they do not enforce the constraint that every occurrence of a variable in logical form be outscoped by the variable's binder. Adding appropriate side conditions to the rules, following the constraints discussed by Hobbs and Shieber [8] would not be difficult.



Next: Postponing Lexical Choice Up: Extensions Previous: Completeness and Coherence
Gertjan van Noord
Thu Nov 24 18:39:44 MET 1994