

Next: The replace operator.
Up: Regular Expression Operators in
Previous: Lenient Composition.
Another application of the priority union operator is in spell
checking. As in [4] we consider a
finite-automaton approach. Suppose we are given a dictionary in the
form of a transducer. The transducer will map each word to its
lexicographic description. A spell checker attempts to
find, for a given word, the lexicographic description of the word
which is closest to a word in the dictionary according to some
distance function. As in many spell checkers we assume Levenshtein
distance: the minumum number of substitutions, deletions and
insertions that is required to map a string into another. In FSA all
strings with a Levenshtein distance of 1 can be defined as follows;
here X can be thought of as the dictionary, lev1(X) is the
Levenshtein-1 closure of the dictionary:
![\begin{displaymath}
\begin{minipage}[t]{.9\textwidth}\begin{verbatim}macro(lev1(X), { subs(X), del(X), ins(X) })\end{verbatim}\end{minipage}\end{displaymath}](img22.gif) |
(20) |
The operators subs/1, del/1 and ins/1 are built-in. The
expression subs(X) stands for all pairs (x,y) such that
(x',y) is in the relation defined by X and x' can be formed
from x by a single substitution. The insertion and deletion
operators are defined likewise.
In contrast to [4] we want to obtain
the candidates with minimal distance. For instance, if we attempt
to lookup book then we don't want to get the description of
cook as a result. This can be defined using the priority union
operator as follows:
![\begin{displaymath}\begin{minipage}[t]{.9\textwidth}\begin{verbatim}macro(spell1(X), priority_union(X, lev1(X)))\end{verbatim}\end{minipage}\end{displaymath}](img23.gif) |
(21) |
For instance, applying spell1 to a dictionary consisting of
the identity transducer over the words book, look, lock, oak
would map each of these words to itself, and in addition it would
map a form such as wook to the set book, look and a
form such as ook to the set book, look, oak.
We can define expressions for any given radius 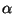 . For example,
the case which treats
. For example,
the case which treats 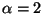 is given by:
is given by:
![\begin{displaymath}\begin{minipage}[t]{.9\textwidth}\begin{verbatim}macro(spel...
...ty_union(spell1(X), lev1(lev1(X))))\end{verbatim}\end{minipage}\end{displaymath}](img26.gif) |
(22) |


Next: The replace operator.
Up: Regular Expression Operators in
Previous: Lenient Composition.
2000-07-03
![]() . For example,
the case which treats
. For example,
the case which treats ![]() is given by:
is given by: