Next: Bottom up generators Up: Problems with existing Previous: Problems with existing
A major problem for top-down generators: left recursion
In this section I will assume a general generation strategy, where rules are applied in a top-down fashion. The order in which nonterminals are expanded can be important. I will assume that this ordering is defined in a satisfactory way. Dymetman & Isabelle 1988 propose a version of DCG where the order of the goals of the body of a DCG clause is defined in two ways: one for parsing and one for generation. Furthermore some version of goal freezing (Colmerauer 1982) is used in cases where this scheme is not powerful enough. The LFG generator of Wedekind 1988 checks whether the resulting daughters of a rule are connected , before this rule can be applied. A node is connected iff its semantics is instantiated. Connectedness not only influences the order of expansion of nonterminals, but also influences the order in which rules are selected. This constraint therefore excludes some useful analyses, as will be shown in the following. Top-down strategies where rules are applied nondeterministically will not terminate for these analyses.
To introduce the problem for top-down generators grammar rule <1> will be considered first.
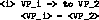
This rule shows that generation is undecidable in general 
.
The rule states that a VP can be combined with the
lexical entry 'to'. The result is a VP that has the same
feature structure.
This example (albeit unrealistic) shows that for some type of
grammars the generation process is undecidable because for
every VP we can add the word 'to' as often as we want (e.g.
generating strings like "john likes to to to to kiss mary").
In most natural language grammars syntactic information
will be available to stop this source of infinite ambiguity.
Often however this information is only available after lexical
lookup.
Therefore a top-down generator may fail to terminate
for some grammars, although syntactic
information is available that should have blocked this type
of undecidability.
I will discuss an example within PATR II, in which
an analysis of subcategorization in HPSG style is used.
The crucial rule is given in <2>, a complete grammar can
be found in appendix A (sample grammar 3) in Shieber 1986.
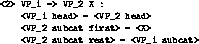
In this analysis subcategorization is expressed
by associating each word in the lexicon with a list of arguments
(the 'subcat' feature in the example). These arguments
are selected one at a time with rules like <2>.
Notice that there is no upper limit to the length of this list.
Syntactic information blocks infinite ambiguities, because the
subcat list will have some fixed length.
This length is specified for each word in the lexicon.
Top-down generators cannot use this syntactic
information because this information is rooted in the lexicon.
The lexicon for example specifies that the subcat list of the
verb 'kiss' has two members.
However, this information is not available until the
lexical entry 'kiss' is reached.
The generation process will also predict longer subcat
lists, without the possibility to
know that these lists will never be realized in a lexical entry.
At a certain moment in the generaton process rule
<2> can be applied to a feature structure that
can be unified with feature structure VP_1.
As a result, rule <2> can also be applied to VP_2, and so
on.
For the LFG-generator of Wedekind this analysis is impossible;
in his approach rule <2> can never be applied because node X will
be unconnected.
For the DCG-generator of Dymetman & Isabelle the generation
process will indeed not terminate.
The problem displays some similarities with the problem
of left recursion for top-down parsing strategies; therefore
I will call this problem the left recursion problem for
top-down generation
.
Note that the problem arises because there is no limit to the size of the subcategorization list. Although one might propose an upper limit for lexical entries, it is linguistically wrong to pose an upper limit in general because subcat lists may be appended in syntax resulting in indefinitely long subcat lists, e.g. in analyses of Dutch crossing dependencies phenomena (Evers 1975, Huybrechts 1984), but also in analyses of Verb Clusters in other languages (Evers 1987). Consider the Dutch sentence <3a>.
In this construction verbs can combine their
subcat lists, as can be seen from <3b>.
Therefore subcat lists can have any length.
It is also impossible to predict from a semantic structure that
contains e.g. 'kiss' the size of its subcategorization list by
looking in the lexicon directly.
It can be the case that the verb will be combined with another
verb, resulting in a longer subcategorization list.
Next: Bottom up generators Up: Problems with existing Previous: Problems with existing
Gertjan van Noord
Fri Nov 25 13:48:52 MET 1994