plot(lls$BAC, lls$ratingNL, xlab='BAC', ylab='rating (NL)')Statistiek I
Introduction to linear regression
Question 1: last lecture
Last lecture
- How to reason about the population using a sample (CLT)
- Calculating the standard error (\(SE\))
- Standard error: used when reasoning about the population using a sample
- Standard deviation: used when comparing an individual to the population
- Calculating a confidence interval
- Specifying a concrete testable hypothesis based on a research question
- Specifying the null (\(H_0\)) and alternative hypothesis (\(H_a\))
- Conducting a \(z\)-test and using the results to evaluate a hypothesis
- Definition of a \(p\)-value: probability of data given that \(H_0\) is true
- Evaluating the statistical significance given \(p\)-value and \(\alpha\)-level
- Difference between a one-tailed and a two-tailed test
- Type I and II errors
This lecture
- Introduction to data used in this lecture
- Correlation as a descriptive statistic
- Introduction to simple linear regression
- Effect size
- How to report on a regression analysis
Introduction to data used in this lecture
Lowlands Science 2018 data
- RQ: Is there a different influence of alcohol (BAC) on L1 vs. L2 language proficiency?
- Hypothesis (alternative): BAC has a stronger negative effect on L1 than L2
- Note: not possible to evaluate in this lecture (but later in this course)
- Instead, we assess here whether there is a negative effect of BAC on L1 only
- Hypothesis (alternative): BAC has a stronger negative effect on L1 than L2
- BAC and L1 and L2 speech samples collected for about 90 native Dutch speakers
- Dutch speech samples were rated by native Dutch speakers (at Lowlands)
- English speech samples were rated by native American English speakers (online)
- For each speaker, the ratings were averaged per language
- Final ratings were \(z\)-transformed (subtract mean and divide by standard deviation)
- Other variables we collected included sex, education level, etc.
- We evaluate the influence of BAC on L1 proficiency for 43 speakers with BAC > 0
Relation between two numerical variables
- We can visualize this relationship in a scatter plot
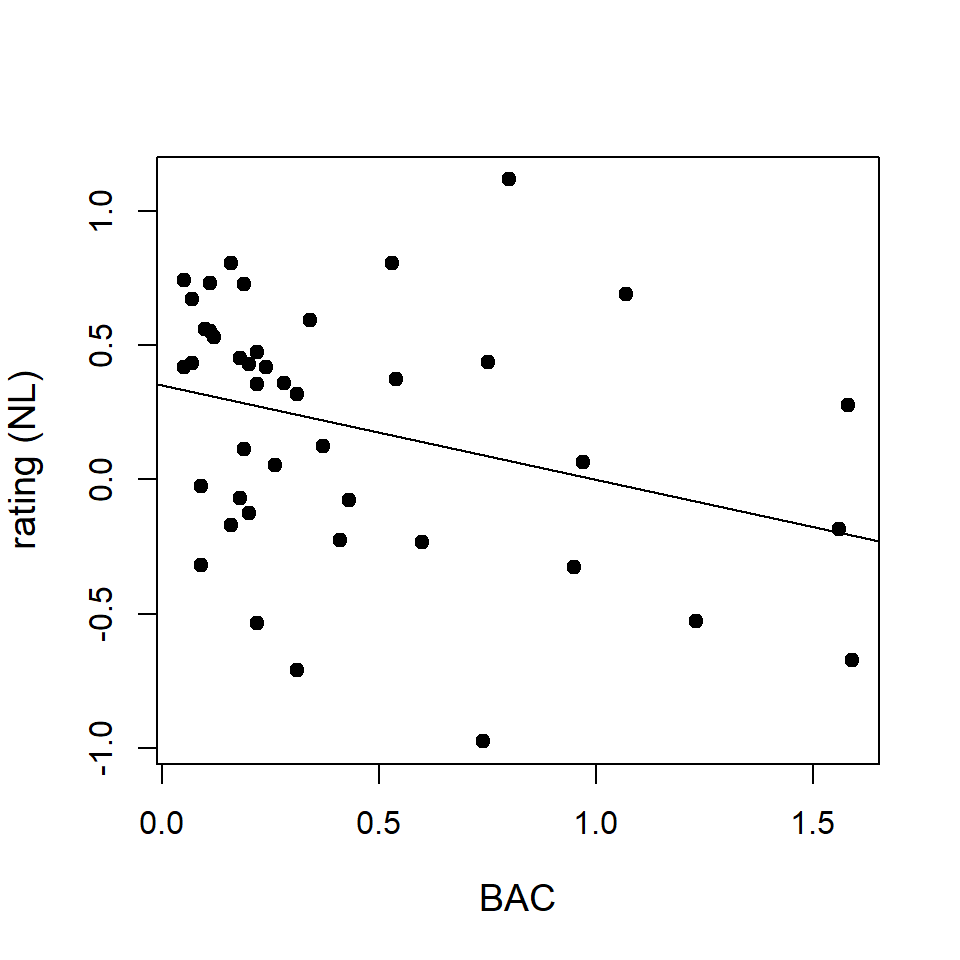
Quantifying the relationship descriptively
- We can quantify the relationship between two variables \(x\) and \(y\) by calculating the Pearson correlation coefficient \(r\)
- Values range between \(-1 \leq r \leq 1\): strength and direction of the effect
Correlation results
Question 2
Correlation demo: sensitivity to outliers
Question 3
(Cor)relation is not causation (1)

(Cor)relation is not causation (2)
- Shoe size and reading ability are correlated
- Is there a dependency between the two?
- No: the hidden variable age affects both shoe size and reading ability!
- Experiments are necessary to control for potential causes (and confounding factors)
From correlation to regression
- In this course, we are using correlation only descriptively
- We use linear regression to statistically assess the relationship between one or more independent variables (predictors) and a dependent variable
- \(H_0\) for linear regression: no effect of independent variable(s) on dependent variable
- We only focus on numerical variables in this lecture
Linear regression: formula
- Linear regression captures a linear relationship between dependent variable (DV) and independent variable(s) (IV)
- Regression formula \(y = \beta_0 + \beta_1 x + \epsilon\)
- \(y\): dependent variable (= predicted or fitted values), \(x\): independent variable
- \(\beta_0\): intercept (value of \(y\) when \(x = 0\)), \(\beta_1\): influence (slope) of \(x\) on \(y\)
- \(\epsilon\): errors (residuals)
- Regression formula \(y = \beta_0 + \beta_1 x + \epsilon\)

Question 4
Residuals: difference between actual and fitted values
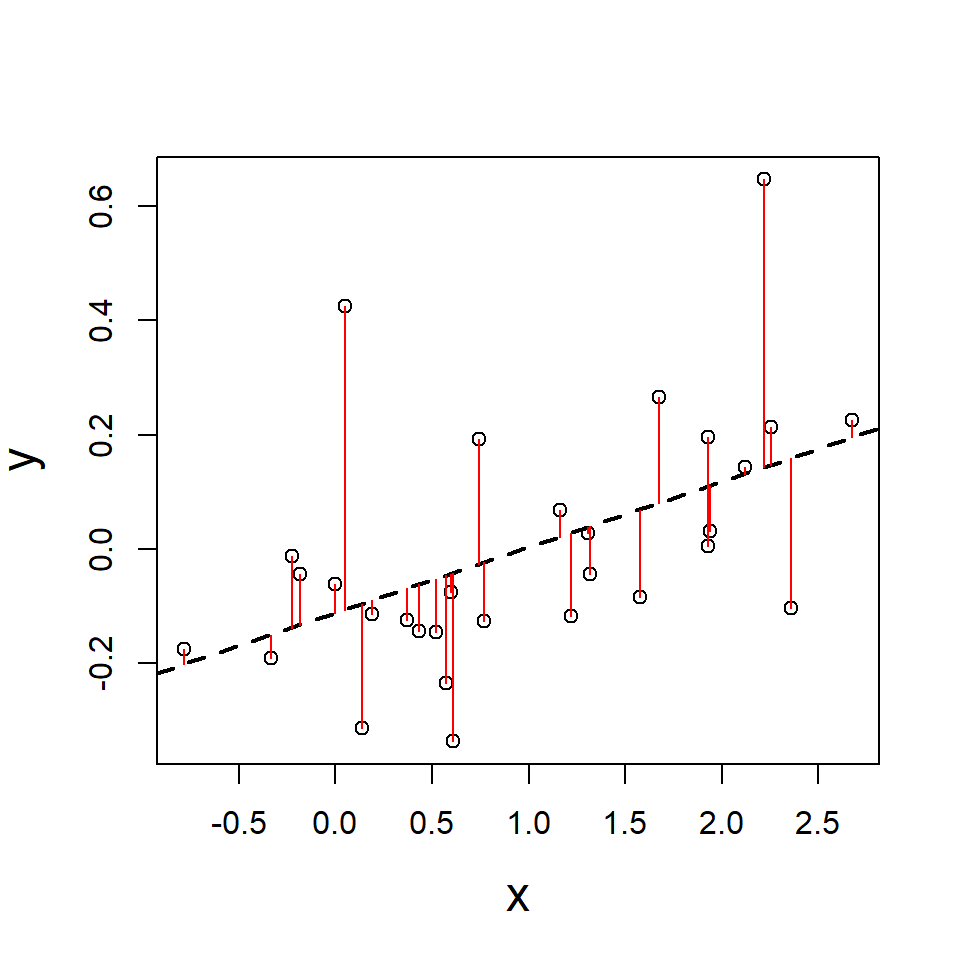
- Regression minimizes residual error (residuals: sum of squared errors)
- Thereby determining the optimal coefficients for intercept and slope(s)
Linear regression: minimizing the residuals
Visualization is essential!
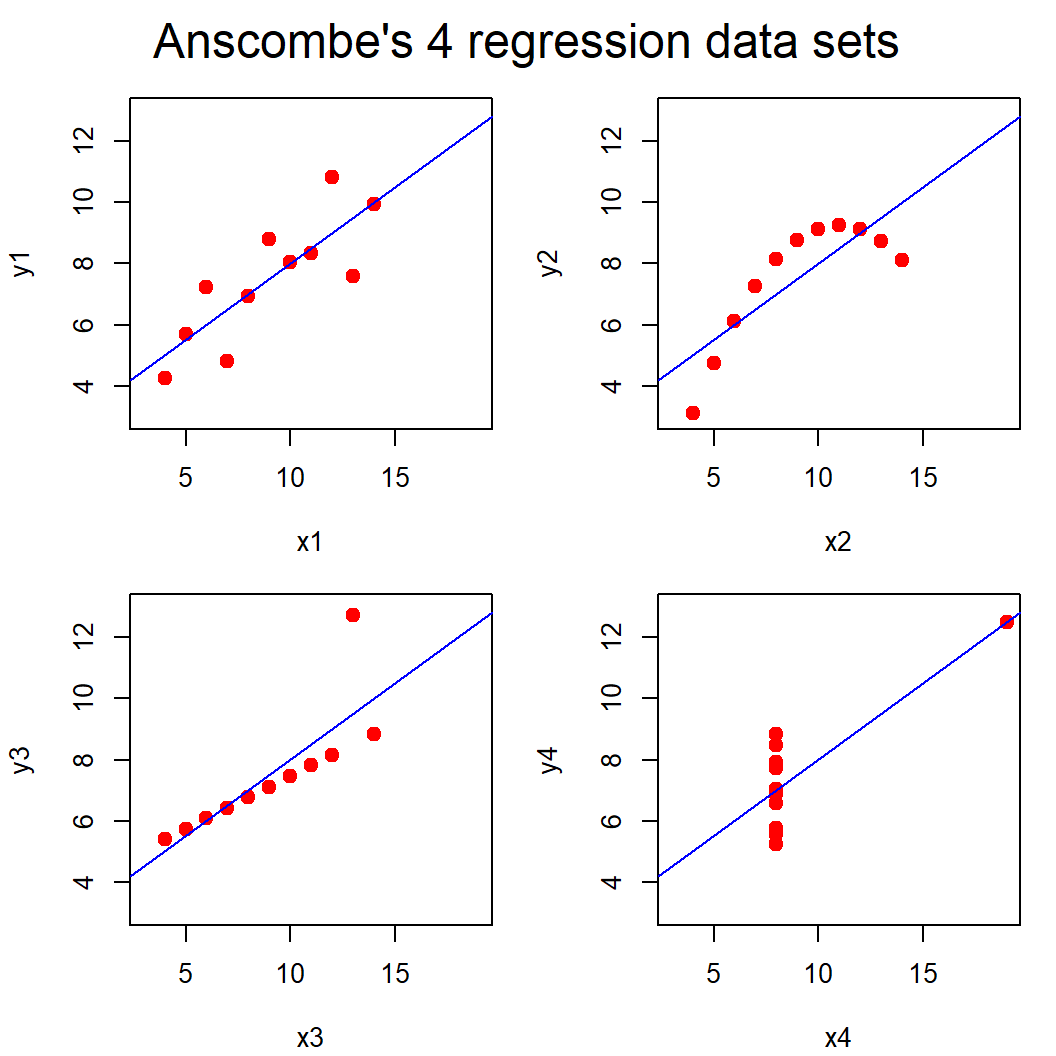
- Linear regression is only suitable in the top-left situation
Fitting our first simple linear regression model in R
Call:
lm(formula = ratingNL ~ 1 + BAC, data = lls)
Residuals:
Min 1Q Median 3Q Max
-1.0653 -0.3496 0.0867 0.2953 1.0466
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.3497 0.0995 3.51 0.0011 **
BAC -0.3505 0.1624 -2.16 0.0369 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.456 on 41 degrees of freedom
Multiple R-squared: 0.102, Adjusted R-squared: 0.0801
F-statistic: 4.66 on 1 and 41 DF, p-value: 0.0369Visualizing the results
Interpretation
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.34970 0.099513 3.5141 0.0010909
BAC -0.35049 0.162448 -2.1576 0.0368728- Summary shows \(\beta_\textrm{bac} =\) -0.35
- For every increase of BAC with 1,
ratingNL(dependent variable) decreases by 0.35
- For every increase of BAC with 1,
- Summary shows \(\beta_0\) (intercept) \(=\) 0.35
- Someone with a
BACof 0 is expected to have aratingNLof 0.35
- Someone with a
- Fitted (predicted) value of the model can be determined using regression formula
- \(y = \beta_0 + \beta_1 x \implies\)
ratingNL = 0.35 + -0.35 * BAC
- \(y = \beta_0 + \beta_1 x \implies\)
Using the regression formula
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.34970 0.099513 3.5141 0.0010909
BAC -0.35049 0.162448 -2.1576 0.0368728- For
BACof \(0\) fittedratingNLof: \(0.35 +\,\) \(-0.35\, *\) \(0\) \(=\) \(0.35\) (= Intercept) - For
BACof \(0.5\) fittedratingNLof: \(0.35 +\,\) \(-0.35\, *\) \(0.5\) \(=\) \(0.175\) - For
BACof \(1.5\) fittedratingNLof: \(0.35 +\,\) \(-0.35\, *\) \(1.5\) \(=\) \(-0.175\)
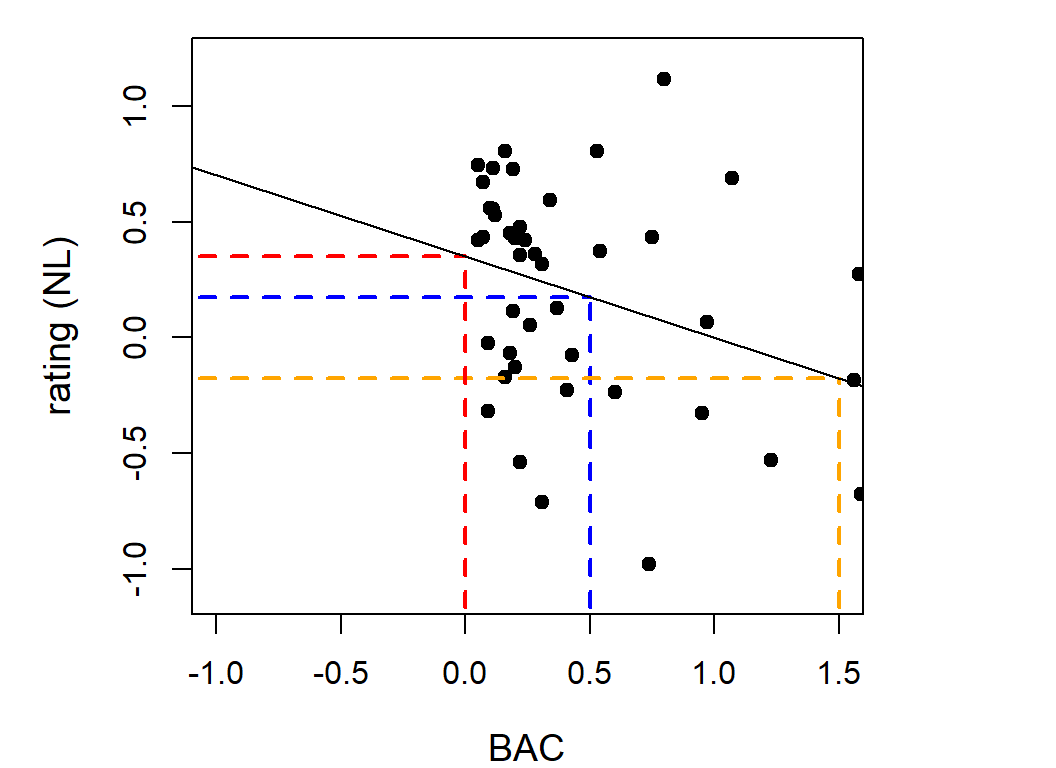
Towards a more meaningful intercept
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.35 0.0995 3.51 0.00109
BAC -0.35 0.1624 -2.16 0.03687- The intercept indicates that people with a BAC of 0 have an expected L1 rating of 0.35
- As sober people were excluded when fitting the model, this value is not so informative
- As sober people were excluded when fitting the model, this value is not so informative
- To make it more meaningful, it is useful to center BAC by subtracting the mean value
Centering the independent variable
lls$BAC.c = lls$BAC - mean(lls$BAC) # center BAC
summary(mc <- lm(ratingNL ~ BAC.c, data=lls))$coef # results with centered BAC Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.196 0.0695 2.82 0.00736
BAC.c -0.350 0.1624 -2.16 0.03687- Intercept now shows that people with an average BAC (
BAC = 0.44 => BAC.c = 0) have an expected L1 rating of 0.196- This is a meaningful value in the context of our data
- (Usually the intercept is not involved in hypotheses, however)
- Note that the coefficient (\(\beta\)) and \(p\)-value of the slope did not change due to centering!
Question 5
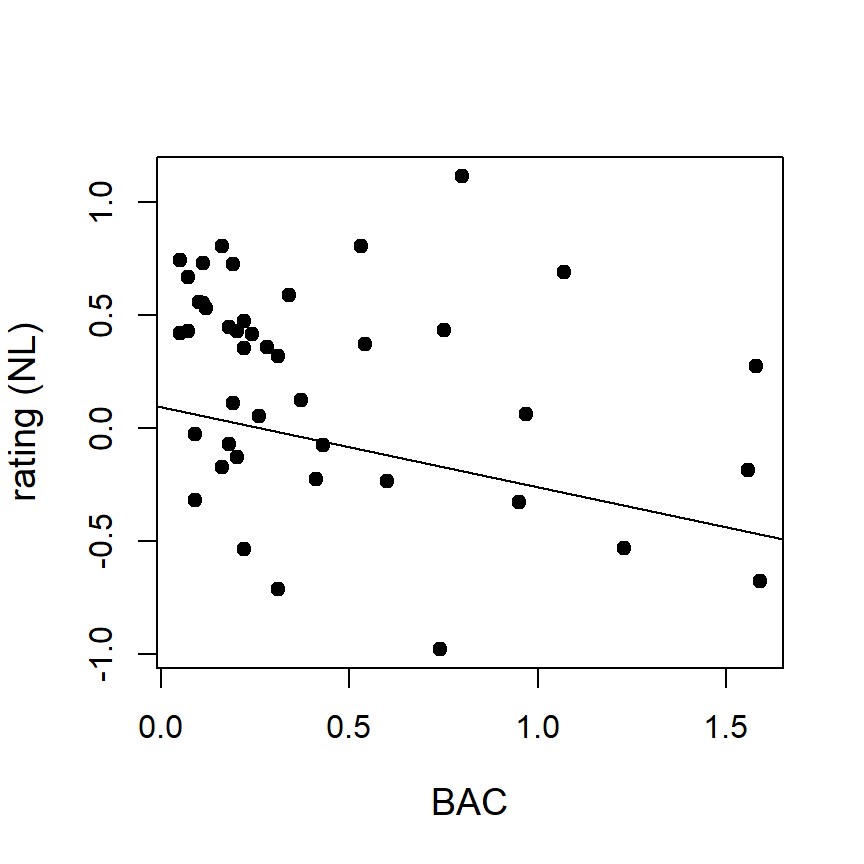
Visual comparison: shifted \(y\)-axis
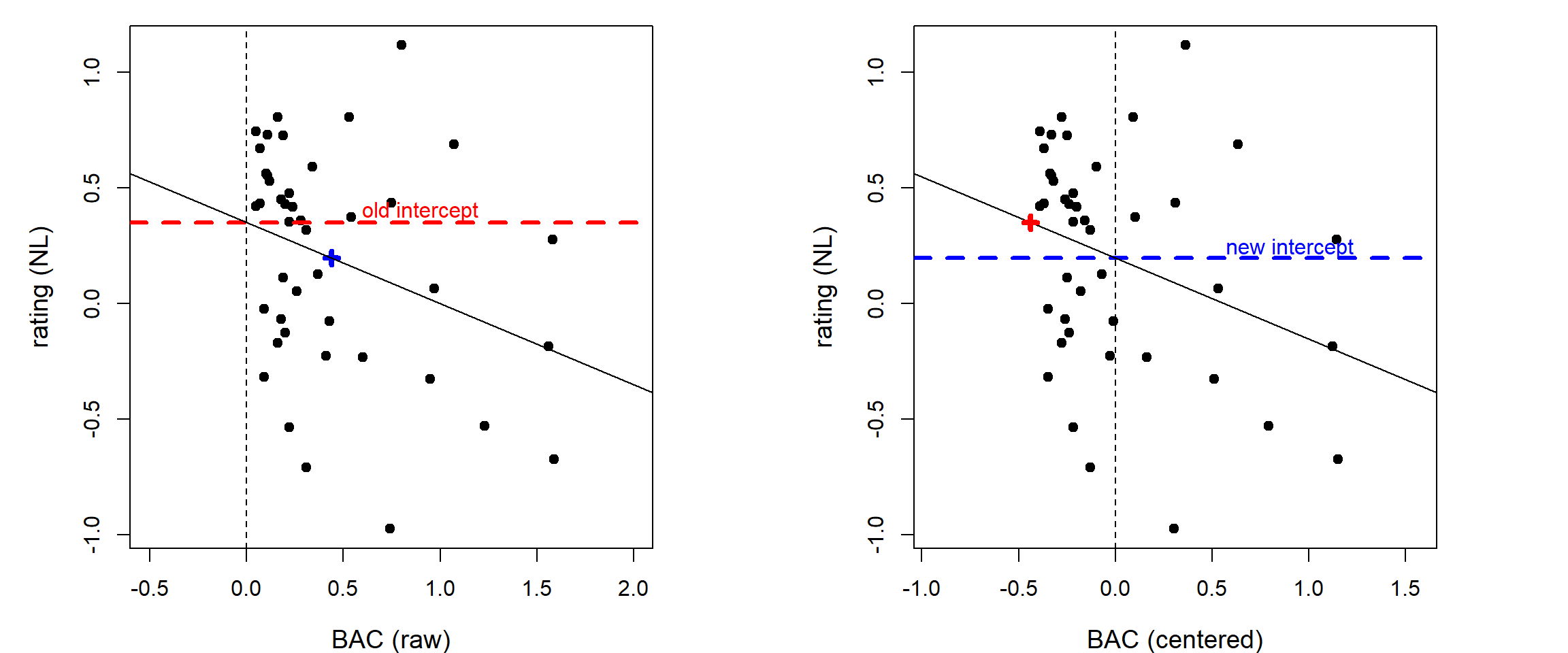
Creating a more meaningful slope
- Interpretation of slope: if BAC increases with 1,
ratingNLdecreases by 0.35 - Not always easy to interpret as scales of independent variables may be very different
- Standardization (\(z\)-transforming) helps interpretation (and facilitates comparison)
lls$BAC.z = (lls$BAC - mean(lls$BAC)) / sd(lls$BAC) # z-transform BAC values
summary(mz <- lm(ratingNL ~ BAC.z, data=lls))$coef # results with z-transformed BAC Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.196 0.0695 2.82 0.00736
BAC.z -0.152 0.0704 -2.16 0.03687- Interpretation of slope (for \(z\)-transformed BAC): if BAC increases with 1 standard deviation (\(\approx\) 0.43), the L1 rating decreases by 0.152
- Note that the \(p\)-value of the independent variable remains unchanged
Visual comparison of the three models
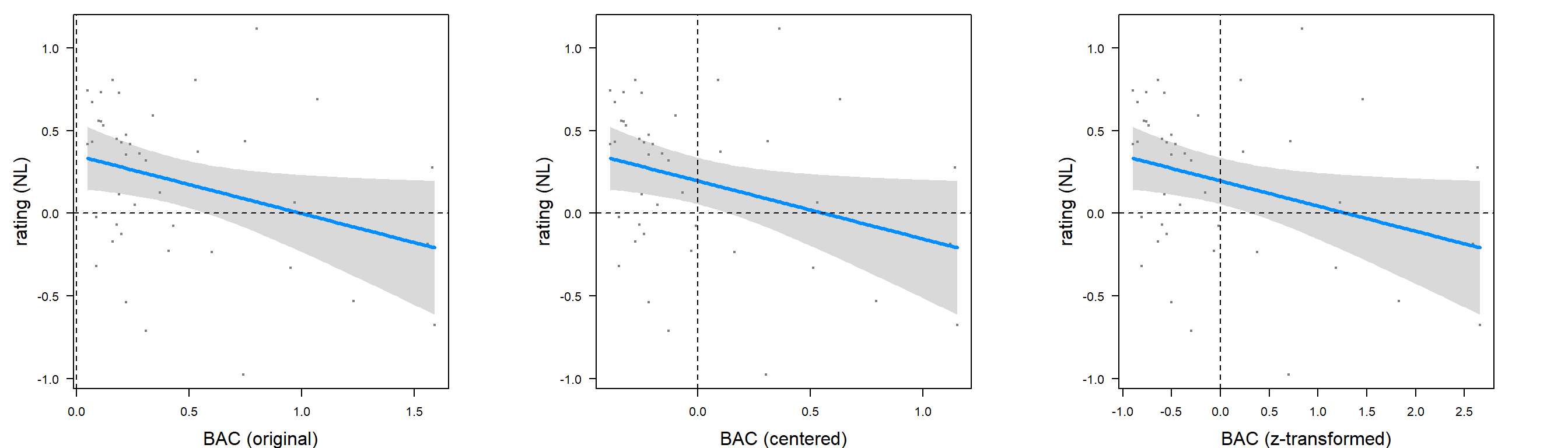
Testing hypotheses using a regression model
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.196 0.0695 2.82 0.00736
BAC.z -0.152 0.0704 -2.16 0.03687- Slope coefficients are relevant for assessing hypotheses
- Here: \(H_0\): \(\beta_\text{bac} = 0\), \(H_a\): \(\beta_\textrm{bac} < 0\)
- Summary shows \(\beta_\textrm{bac} =\) -0.15
- Associated two-sided \(p\)-value is 0.037
- Hypothesis is one-sided, and coefficient in line with \(H_a\), so \(p\)-value = \(\frac{0.037}{2} \approx 0.0185\)
- \(p\)-value < 0.05 (\(\alpha\)) \(\implies\) reject \(H_0\) and accept \(H_a\)
- There is a significant negative effect of BAC on L1 pronunciation
Background: how are \(p\)-values determined in regression?
- Last lecture: \(z\)-values can be used to determine a \(p\)-value
E.g., \(z \geq 2 \implies p \approx 0.025\)
But \(z\)-values can only be determined when \(\sigma\) is known
- When \(\sigma\) is not known, we can estimate it using the sample standard deviation \(s\)
- Using \(s\), we can determine the \(t\)-value, which is comparable to the \(z\)-value
Determining the \(t\)-value
- Recall the formula to determine the \(z\)-value for a sample:
\[z = \frac{m - \mu}{\sigma / \sqrt{n}}\]
- The only difference between determining the \(t\)-value compared to the \(z\)-value is the way the standard error \(SE\) is computed:
\[SE = s / \sqrt{n}\]
- For regression, we always assume \(\mu\) to be 0 (\(H_0\): no effect of a predictor), and for \(m\) we use the estimated regression coefficient \(\beta\), yielding the following formula for \(t\):
\[t = \frac{\beta}{SE}\]
Manually checking the \(t\)-values
Obtaining \(p\)-values on the basis of \(t\)-values
- To determine a \(p\)-value, \(z\)-values are compared to the standard normal distribution
- But \(t\)-values are compared to the \(t\)-distribution
- \(t\)-distributions look similar to the standard normal distribution
- But dependent on the number of degrees of freedom (dF)
What are degrees of freedom?
- There are five balloons each having a different color
- There are five students (\(n = 5\)) who need to select a balloon
- If 4 students have selected a balloon (dF = 4), student nr. 5 gets the last balloon (fixed)

- If 4 students have selected a balloon (dF = 4), student nr. 5 gets the last balloon (fixed)
- Similarly, if we have a fixed slope and a fixed intercept with 43 observations
- 41 values may vary, but the 42nd and 43rd are fixed: dF = 43 - 1 - 1 = 41
- For regression, dF = N - V - 1 (with N: nr. of obs., V: nr. of independent variables)
Question 6
\(t\)-distribution vs. normal distribution
- Difference between normal distribution and \(t\)-distribution is large for small dFs
- When dF \(\geq\) 100, the difference is negligible
- As the shape differs, the \(p\)-value associated with a certain \(t\)-value also changes
Visualizing \(t\)-distributions
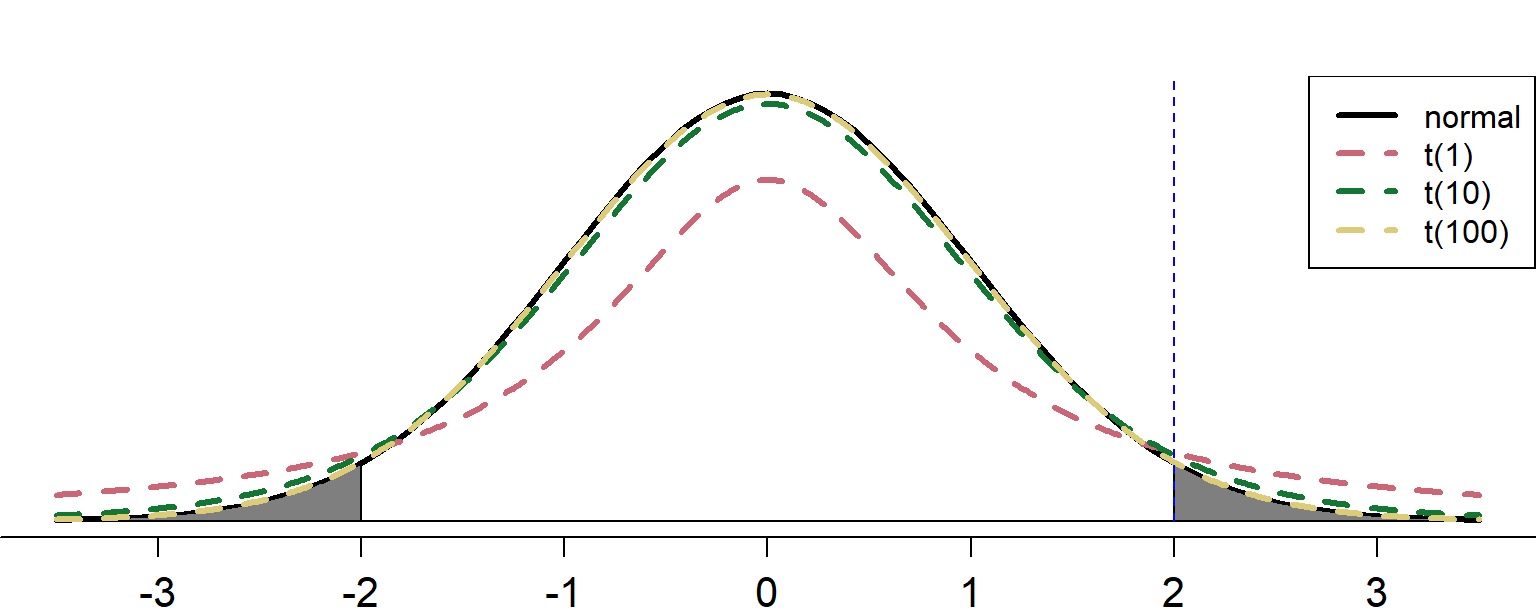
- For significance (given \(\alpha\)), higher (abs.) \(t\)-values are needed than \(z\)-values (but only when dF < 100, otherwise \(z\) and \(t\) are equal)
Question 7
Answer to question 7
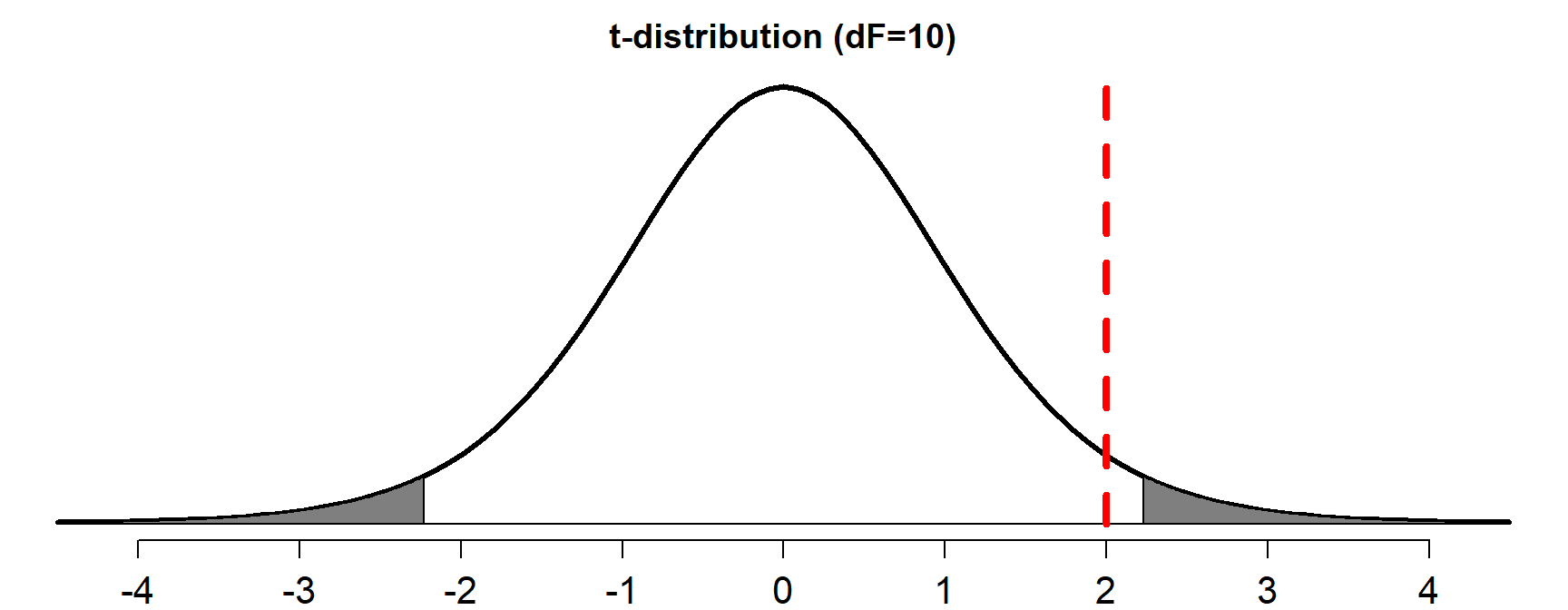
- Dark gray area: \(p\) < 0.05 (2-tailed)
Calculating \(p\)-values manually for our model
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.35 0.0995 3.51 0.00109
BAC -0.35 0.1624 -2.16 0.03687[1] 0.00109[1] 0.0368693- Manual computation is not needed as
Rdoes it for us- But you have to understand the idea behind it!
Other components of the regression model summary
Call:
lm(formula = ratingNL ~ 1 + BAC, data = lls)
Residuals:
Min 1Q Median 3Q Max
-1.0653 -0.3496 0.0867 0.2953 1.0466
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.3497 0.0995 3.51 0.0011 **
BAC -0.3505 0.1624 -2.16 0.0369 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.456 on 41 degrees of freedom
Multiple R-squared: 0.102, Adjusted R-squared: 0.0801
F-statistic: 4.66 on 1 and 41 DF, p-value: 0.0369- You can ignore the remaining parts, except for the line with the R-squared values
Effect size: \(R^2\) of the model
- \(R^2\): proportion of variation of the DV explained by the IV(s) in the model
- \(R^2\) ranges from 0 to 1, with higher being better (perfect prediction: 1)
- Effect size magnitudes: small (\(R^2 \approx 0.01\)), medium (\(R^2 \approx 0.1\)), large (\(R^2 \gtrapprox 0.25\))
- When the model contains a single IV, \(R^2\) is the effect size of that variable
- (Adjusted \(R^2\) is used instead when multiple independent variables are present)
Correlation and \(R^2\)
- \(R^2\) of a linear regression model with 1 independent variable (IV) and 1 dependent variable (DV) equals the square of Pearson’s correlation
[1] -0.31931[1] 0.10196Model assumptions for linear regression
- Two important requirements:
- Distribution of residuals is assumed to follow a normal distribution
- Variance of residuals should be equal along the regression line (homoscedastic)

Does our model satisfy the required assumptions?
Reporting results
Our RQ was: Does alcohol have a negative influence on L1 language proficiency? Our hypotheses were: \(H_0\): \(\beta_{bac} = 0\), \(H_a\): \(\beta_{bac} < 0\). We obtained alcohol percentages and L1 proficiency ratings for 43 individuals. We fitted a regression model with the L1 ratings as the dependent variable (DV) and blood alcohol concentration (BAC) as the independent variable (IV). We verified that the required assumptions were satisfied (i.e. normally distributed and homoscedastic residuals). The regression coefficient for BAC was -0.35 with a one-tailed associated \(p\)-value of 0.018. The effect size, measured in \(R^2\) was 0.102 (medium). This indicates that the predictor BAC accounts for about 10% of the variance in L1 proficiency ratings. See Table X and Figure Y for the exact pattern. As the \(p\)-value was lower than our significance threshold \(\alpha\) of 0.05, we reject the null hypothesis and accept the alternative hypothesis that there is a significant negative influence of alcohol on L1 language proficiency.
Summary: assessing significance and reporting results
- Describe RQ, \(H_0\) and \(H_a\)
- Indicate how and what data was collected and the sample size
- Indicate the dependent variable (DV) and the independent variable (IV)
- Report whether requirements for residuals satisfied (normal and homoscedastic)
- Report the estimates and \(p\)-values (and provide all details in a table)
- Visualize the results
- Report effect size
- Observe the \(p\)-value (adjust for one-tailed hypothesis), compare to \(\alpha\) (report!) and determine your conclusion
- \(p\)-value \(< \alpha\), significant result: reject \(H_0\) and accept \(H_a\)
- \(p\)-value \(\geq \alpha\), non-significant result: retain \(H_0\)
Practice this in laboratory exercises!
Recap
- In this lecture, we’ve covered
- Correlation
- Linear regression with a single numerical variable
- Correlation
- Next lecture: Multiple linear regression (including nominal variables)
Please evaluate this lecture!
Exam question
Questions?
Thank you for your attention!
https://www.martijnwieling.nl
m.b.wieling@rug.nl

