Subsections

• Theorem

Definite clauses of $\cal {R}$($\cal {L}$)

I follow the construction defined by [32] to extend $\cal {L}$, giving $\cal {R}$($\cal {L}$), by adding a set of relation symbols $\cal {R}$, conjunction, negation and existential quantification. The syntax I use for these will be clear from the definition of the interpretations of $\cal {R}$($\cal {L}$) (essentially Prolog syntax where appropriate).

The interpretation $\cal {A}$ of $\cal {R}$($\cal {L}$) is defined in terms of the interpretation $\cal {I}$ of $\cal {L}$. The expression $\alpha$[s $\leftarrow$ X] defines the assignment which is exactly like $\alpha$, except possibly for the variable X which gets assigned the element s. An interpretation $\cal {A}$ of $\cal {R}$($\cal {L}$) is obtained from $\cal {I}$ ($\cal {A}$ is said to be based on $\cal {I}$) by choosing for every relation symbol r $\in$ $\cal {R}$ a relation r^{$\cal {A}$} on $\cal {D}$^{$\cal {I}$} taking the right number of arguments. Furthermore, let

1.

$\cal {D}$^{$\cal {A}$} = _def$\cal {D}$^{$\cal {I}$};

2.

$\phi^{\cal{A}}_{}$ = _def$\phi^{\cal{I}}_{}$; for $\phi$ a $\cal {L}$ constraint.

3.

r($\vec{x}\,$)^{$\cal {A}$} = _def{$\alpha$ $\in$ ASS^{$\cal {A}$}|$\alpha$($\vec{x}\,$) $\in$ r^{$\cal {A}$}};

4.

for the empty conjunction $\emptyset$, $\emptyset^{\cal{A}}_{}$ = _defASS^{$\cal {A}$};

5.

(F, G)^{$\cal {A}$} = _defF^{$\cal {A}$} $\cap$ G^{$\cal {A}$};

6.

($\neg$F)^{$\cal {A}$} = _defASS^{$\cal {A}$} - F^{$\cal {A}$};

7.

($\exists$X.F)^{$\cal {A}$} = _def{$\alpha$[s $\leftarrow$ X]|$\alpha$ $\in$ F^{$\cal {A}$}, s $\in$ $\cal {D}$^{$\cal {A}$}}

Implication, universal quantification and disjunction may be defined in terms of these connectives. The formalism consists of definite clauses of $\cal {R}$($\cal {L}$). I write such a definite clause as:

$$\mbox{\it p} \mbox{\tt :-} \mbox{\it q}_{1}, \dots , \mbox{\it q}_{n}, \phi.$$
where p,q₁...q_n are atoms and $\phi$ is a $\cal {L}$ constraint. Atoms look as r(X₁,...,X_n) where r $\in$ R and X₁...X_n $\in$ V.

A partial order on the set of all $\cal {R}$($\cal {L}$) interpretations is defined as follows: $\cal {A}$ $\subseteq$ $\cal {B}$ iff for all r $\in$ R,r^{$\cal {A}$} $\subseteq$ r^{$\cal {B}$}. The union of a set of $\cal {R}$($\cal {L}$) interpretations is obtained by joining the denotations of the relation symbols and is again an $\cal {R}$($\cal {L}$) interpretation. A model M of a set of definite clauses $\cal {S}$ is defined as an $\cal {R}$($\cal {L}$) interpretation such that M satisfies $\cal {S}$, i.e., $\cal {S}$^M = ASS^M.

The use of definite clauses is motivated by the following theorem, proven in [32] for the general case.

Theorem

Let $\cal {S}$ be a set of definite clauses in $\cal {R}$($\cal {L}$), and $\cal {I}$ a $\cal {L}$ interpretation. Define for all r $\in$ $\cal {R}$

$$\mbox{\it r}^{{\cal{A}}_{0}} =_{def} \emptyset,$$

$$\mbox{\it r}^{{\cal{A}}_{i+1}} =_{def} \{\alpha \vert (\mbo... ...x{\tt :-} G) \in {\cal{S}} \wedge \alpha \in G^{{\cal{A}}_i}\}$$
This defines a chain $\cal {A}$₀ $\subseteq$ $\cal {A}$₁ $\subseteq$ ... of $\cal {R}$($\cal {L}$) interpretations, based on $\cal {I}$. Moreover, the union

$$\bigcup_{i \geq 0} {\cal{A}}_i$$
is the least model of $\cal {S}$ extending $\cal {I}$.

This theorem says that if $\cal {S}$ is a set of definite clauses, then $\cal {S}$ uniquely defines the relations of $\cal {R}$; i.e. $\cal {S}$ defines unique minimal denotations for the relation symbols of $\cal {R}$.

Example 10   As an example, let C = {c}, L = {l}, V = {XX₁...} and R = {p,q}. Furthermore, consider the following definite program:

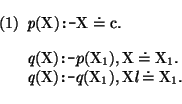
Clearly, p^{$\cal {A}$₀} and q^{$\cal {A}$₀} are both the empty set. Because the assignments are based on $\cal {I}$ we know the solutions of the constraints. Therefore, we obtain

$$\cal {A} \alpha \alpha \in \doteq \cal {A}$$ =

$$\alpha \alpha \in \doteq \cal {I}$$ =

$$\alpha \alpha \alpha$$ =

$$\emptyset$$ =

But the denotation of the relation q is still empty. In the next round, it is clear that p^{$\cal {A}$₂} = p^{$\cal {A}$₁}. The denotation of the relation q becomes interesting now:

$$\cal {A} \alpha \alpha \in \doteq \cal {A}$$ =

$$\alpha \alpha \in \cal {A} \cap \doteq \cal {A}$$ =

$$\alpha \alpha \emptyset \wedge \alpha \alpha$$ =

$$\emptyset$$ =

The process continues like that, and we obtain the following diagram. The feature graphs f₁, f₂, f₃... are those given in figure 2.4.

Figure 2.4: Feature graphs f₁, f₂, f₃...

The denotation of the relation symbols is given by the following figure, where I write c for the feature graph (c,$\emptyset$). ^2.2

	0	1	2	3	4	5	...
p	$\emptyset$	{ c}	{ c}	{ c}	{ c}	{ c}	...
q	$\emptyset$	$\emptyset$	{ c}	{ c, f1}	{ c, f1, f2}	{ c, f1, f2, f3}	...

A goal or query is a possibly empty conjunction of $\cal {R}$($\cal {L}$)-atoms and a $\cal {L}$-constraint, written as:

$$\prologq \mbox{\it p}_{1} \dots \mbox{\it p}_{n}, \phi.$$

An answer to a goal is a satisfiable constraint $\psi$, such that $\psi$ $\rightarrow$ p₁...p_n,$\phi$ is valid (given a set of clauses $\cal {S}$) in the minimal model of $\cal {S}$. For example, for the previous definite clause program a possible answer to the goal

$$\prologq \mbox{\it q}(\mbox{\rm X}_{0})$$
is the answer:

$$\mbox{\rm X}_{0}\mbox{\it l} \doteq \mbox{\rm c}$$
because X₀l $\doteq$ c $\rightarrow$ q(X₀) is valid in the minimal model.