Subsections

• Restricting equivalence to cyclic labels.
• No equivalence for reentrancies.
• Thompson's proposal.

Other versions of the parsing problem

Other definitions of the parsing and generation problems have been defined as well. For example, in [99] two relaxations of the foregoing definition of the p-parsing problem are discussed. Such relaxations may in certain applications allow for simpler grammars.

Restricting equivalence to cyclic labels.

The first relaxation assumes that it is possible to make a distinction between cyclic and non-cyclic labels. A non-cyclic label will be a label with a finite number of possible values (i.e. it is not recursive). For example the labels arg1 and arg2 may be cyclic whereas the label number may be non-cyclic. The completeness and coherence condition can be restricted to the values of cyclic labels. If the proof procedure can only further instantiate acyclic labels no termination problems occur because there are only a finite number of possibilities to do this.

For certain applications this may be useful. For example, consider the case where monolingual grammars define semantic structures which are annotated with some syntactic information as well. If the completeness and coherence conditions are restricted to cyclic labels, the input to the generator may be under-specified with respect to these syntactic decorations. These syntactic labels can then be filled in by the generator on the basis of the monolingual grammar.

No equivalence for reentrancies.

The second relaxation has to do with reentrancies in feature structures. It is possible to define a version of the parsing problem that does not take into account such reentrancies. As will be explained in more detail in section 5.4.2, it turned out that in using 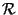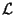$\cal {R}$($\cal {L}$) to define transfer rules in an MT system it was rather cumbersome to be forced to redefine possible reentrancies in transfer rules as they were defined in the monolingual grammar. Therefore, a definition of the p-parsing problem was investigated that did not require completeness and coherence of such reentrancies. The possible usefulness of this conception of the parsing problem will be discussed in section 5.4.2.

Thompson's proposal.

Another possibility is investigated in [92]. The basic intuition of his approach is that the parser (or generator) should come up with those signs that are as close as possible to the input structure. That is, answers to the parsing and generation problem consist of those signs that `minimally extend' the input and `maximally overlap' the input. The notions `minimally extend' and `maximally overlap' are defined with respect to other possible answers to the parsing problem.

The problem with this approach seems to be that, although interesting, the implementation is far from straightforward. The difficulty is increased by the fact that in this approach for the proof procedure to know whether something is an answer to a goal it is necessary to take into account all other possible answers. In the other versions of the parsing problem answers are independent of each other.