In order to extend the determinization algorithm for transducers
[28,30,26,31,32], we
must extend pfst in such a way that the output part of a transition is
a sequence of predicates. This extension is described later, but first
we illustrate some of the complications that arise. For the moment we
will simply assume that the output part of a transition contains a
sequence of predicates. We first create an equivalent pfst which has
no ![]() on the domain part of transitions, using the same
technique as described in [32, page 29].7 In the determinization algorithm,
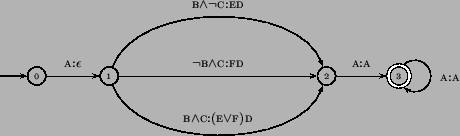
local ambiguities such as those encountered in state 0 in (here,
A...F are arbitrary predicates
on the domain part of transitions, using the same
technique as described in [32, page 29].7 In the determinization algorithm,
local ambiguities such as those encountered in state 0 in (here,
A...F are arbitrary predicates ![]() ):
):
![\begin{pspicture}(-2,-0.5)(9,2.5)
\psset{unit=0.02cm}\rput(0,60.0){\circlenode[]...
...15.0]{->}{4}{2}
\nbput{\rnode{x}{\footnotesize {\sc c}:{\sc d}}}
\end{pspicture}](img118.gif)
are solved by delaying the outputs as far as needed, until these symbols can be written out deterministically:8
The determinization algorithm for transducers maintains sets of
pairs ![]() . Such a set corresponds to a state in the
determinized transducer. In order to compute the transitions leaving
such a set of pairs P, we compute for each
. Such a set corresponds to a state in the
determinized transducer. In order to compute the transitions leaving
such a set of pairs P, we compute for each ![]() ,
,
![]() .
In the example, we can be in states 3 and 4 after reading a symbol
compatible with A, with pending outputs E and F. We thus have
.
In the example, we can be in states 3 and 4 after reading a symbol
compatible with A, with pending outputs E and F. We thus have
![]() . Therefore, we have:
. Therefore, we have:
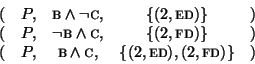
A transition is created from a proto-transition by removing the
longest common prefix of predicates in the target pairs; this
prefix is the sequence of output predicates of the resulting
transition. However, before we remove this longest common prefix, we
first consider possible simplifications in the sequences of output
predicates, by packing multiple sequences associated with the same
target state into a smaller number of sequences (using disjunction).
In particular, two pairs of target state and predicate sequences
![]() and
and ![]() can be combined into a single pair
can be combined into a single pair
![]() iff p1=p2=p and
iff p1=p2=p and
![]() ,
,
![]() and
and
![]() .
In a proto-transition this simplification is applied repeatedly until no
further simplifications are possible.
.
In a proto-transition this simplification is applied repeatedly until no
further simplifications are possible.
Here, the third proto-transition is simplified into:
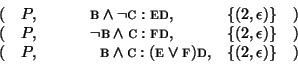
The introduction of predicates thus has the interesting effect that
certain non-functional transducers can be treated by the transducer
determinization algorithm.
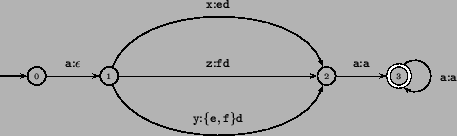
Assume that B is the predicate
![]() ,
C is the predicate
,
C is the predicate
![]() and the predicates
A, D, E and F are true only of the
symbols a, d, e and
f respectively. The equivalent normal transducer is:
and the predicates
A, D, E and F are true only of the
symbols a, d, e and
f respectively. The equivalent normal transducer is:
![\begin{pspicture}(-2,-1)(9,4.5)
\psset{unit=0.02cm}\rput(0,90.0){\circlenode[]{0...
...15.0]{->}{4}{2}
\naput{\rnode{x}{\footnotesize {\tt y}:{\tt d}}}
\end{pspicture}](img137.gif)
This transducer cannot be treated by the transducer determinization algorithm (that algorithm does allow a limited form of ambiguity, but only if this ambiguity can be delayed to a final state; here this is not possible). However, the same transduction can be determinized if expressed by a pfst:
If predicates are used, then a larger class of transductions can be implemented efficiently. A precise classification of this class is beyond the scope of this paper, but note that the type of ambiguities that can be implemented in this way is limited to ambiguities that extend only over a single symbol.9 For instance, a simple example such as the following cannot be determinized:
![\begin{pspicture}(-3.5,-1)(7.5,3.0)
\psset{unit=0.015cm}
\rput(0,60.0){\circleno...
...rc[arcangle=-15.0]{->}{3}{1}
\nbput{\rnode{x}{$\epsilon$:\tt e}}
\end{pspicture}](img140.gif)