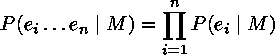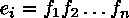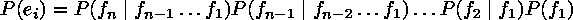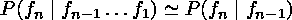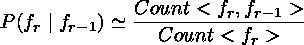How We Did It - Details |
Here is a more in-depth and Mathematical description of how the authorship
identification software works. The
code is written in Perl and may be downloaded.
The Corpora |
Firstly, let's say we have two corpora of texts. The first is composed of the collected lyrics of Paul McCartney, after the Beatles split. Let's call this corpus M. The second corpus is made up of the lyrics of John Lennon songs, from the group's breakup to his death, let's call this one L.
We know have a song with lyrics of unknown authorship,
U.
We want to determine who is the more probable author, Lennon or McCartney.
We therefore create a model for L and M based on their solo
work, then calculate the probability for each model given
U.
Calculating the Model for Lennon (L) |
We obtained the lyrics of John Lennon's subsequent solo work from a web site and concatenated them into a single file. We processed the file to remove all punctuation and hyphens, and to convert all letters to lower case.
Then, we built two word frequency tables, one of UNIGRAMS , and one of BIGRAMS.
| UNIGRAM | An occurence of a single word. |
| BIGRAM | An occurence of a unigram followed by another unigram, a sequence of two words. |
The UNIGRAM table is a list of every word that appears in the corpus L plus the number of times it occurred. The BIGRAM table is a similar list of sequences of two words. We will use the frequency counts for probabiility value calculation later on.
These two profiles constitute the model for Lennon.
Calculating the Model for McCartney (M) |
We processed McCartney's solo work in a similar manner.
Probability Calculation |
We want to find out, given a song of unknown authorship U, who is the more probable author, Lennon (L) or McCartney (M). If we haven't seen a text, we symbolize the probability that Lennon wrote it as P(L). But if we have seen the text, then the probability is different, maybe higher, maybe lower, depending on how much it is like other texts Lennon wrote. We symbolize this P(L|U). This is the probability, given the text, that the author is Lennon. Similarly, the probability that McCartney wrote a given text we symbolize P(M|U). To ask for a best guess as to who wrote a given song is to ask which probability is higher, P(L|U) or P(M|U).
Looking at this another way, we want to see which model is the most "similar" to U, the model L (obtained from the corpus as described above), or the model M. We calculate a probability value for both which is indicative of this "similarity".
The higher value will indicate the identity of the author - L (Lennon) or M McCartney.
Now for some Maths
(DON'T
PANIC!).
Let's say we want to see how likely it is that McCartney wrote song U.
So we want to see if
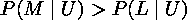
Calculating these probabilities directly is far too difficult, so we simplify using Bayes's law:
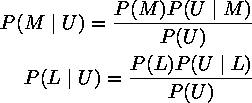
Since P(U) is the same in both formulae, and we have no reason to believe that Lennon is more likely to be the author than McCartney, we can simplify the above formulae to:
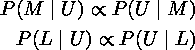
So now we want to find out if:
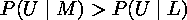
U can be considered a sequence of i lines ei
each containing a sequence of n words fn, all assumed imdependent:
We want the probability:
We can approximate this by calculating:
We estimate this probability by counting the number
of times the bigram frfr+1 and the unigram
fr was seen in the training corpus (Lennon's lyrics for L,
McCartney's lyrics for M), and getting
the value:
The above values can be obtained from the
bigram and unigram tables.
Note: So the calculation boils down to a product of
the word bigram and unigram probabilities. Due to the small numbers
involved we use logs for the calculation. It is also possible to use trigrams
(sequences of three words) etc, but the corpora in this case were too small
to warrant their use.
You may notice that this method falls down as soon as an unknown unigram
or bigram is encountered as this will have a probability of zero.
So, we add an extra unigram to the unigram table called the "unknown"
unigram. Similarly for the bigram table. This will ensure a low but non-zero
probability value is assigned to unknown unigrams and bigrams.
We do the same for L and then select the model
with the highest probability value.