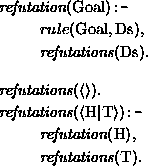 |
Consider the `naive' top-down generation algorithm defined in chapter 2 and repeated here as figure 3.6.
The algorithm simply matches a node with the mother node of some rule and recursively generates the daughters of this rule. The left-to-right search strategy we have been assuming, causes non-termination of this algorithm for the goal:
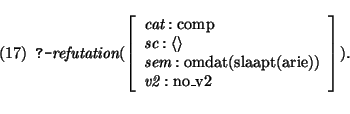
The task is to generate a saturated complementizer phrase. The binary
complementizer rule 7 is the only candidate and may be
applied. After the proper generation of the first daughter of this
rule the generator attempts to generate a saturated verb phrase with
semantics
slaapt(arie). For this embedded generation task the
verb phrase rule 1 is the appropriate candidate. The first
daughter of this rule, however, is not sufficiently instantiated to
guide the search any further: the algorithm may for example apply the
same rule 1 for this node, and will go into an infinite loop
because each time it chooses rule 1 for the first daughter
of rule 1.
Therefore, the order in which nonterminals are expanded is very important, as was noticed by [17] and [108]. If, in the foregoing example, the generator first tries to generate the second daughter, then it may be possible to generate the first daughter without problems afterwards. In the approach of [17], the order of generation is defined by the rule-writer by annotating DCG rules. In the approach of [108], this ordering is achieved automatically (and dynamically), essentially by a version of the goal-freezing technique [13]. Put simply, the generator only generates a node if its feature structure is instantiated; otherwise the generator will try to generate other nodes first.
A specific version of this approach, is an approach where one of the daughters has a privileged status. This daughter, that we might call the `head' of the rule, will always be generated first. I will assume that for all rules the first daughter of the list of daughters represents the head. Note that this does not imply that this daughter is the leftmost daughter; the information about the left-to-right order of daughters is represented by the difference-list representation of strings in each node. Moreover note that this particular representation may be the result of some compilation step from a representation that is more convenient for the rule writer. For example, rule 1 was represented schematically as
![]()
If we assume that the second daughter is the
head, then this clause is simply written:
![]()
Now without any modification to the original definition of refutations this change will imply that heads are generated first.
Assume furthermore that the head of a rule is that daughter which
shares its semantics with the mother node. In all (non-unit) rules of
the Dutch example grammar it is possible to choose such a daughter.
The resulting simple top-down generation algorithm is equivalent to the approaches of [17] and [108] with respect to one major problem: the left-recursion problem. Consider what happens if we try to generate a sentence for the same semantic structure 17 as before, but this time assuming that heads are generated first. Again, the generator comes to the point where it tries to generate a saturated verb phrase with semantics slaapt(arie). As before the generator selects the binary verb phrase rule 1. This time the generator does not try to generate the argument of this rule, but immediately starts to generate its head. The resulting feature structure now looks as follows:

where
Obj1 is shared with the argument that still needs to be
generated after the generation of the head. This feature structure can
be the input for the verb phrase rule 1 again, of which the head will then
be instantiated into:

Each time the same rule can be applied (predicting longer and longer
subcategorization lists), resulting in non-termination, because of
left recursion. It should be clear that this non-termination problem is not
necessarily caused by the leftmost daughter of a rule; the
problem is caused by the node that is generated first. Thus the
English equivalent of the verb phrase rule where the order of the head
and the argument is switched presents exactly the same problem.
In this particular case, the problem arises because there is no limit
to the size of the subcategorization list. Although one might propose
an ad hoc upper bound on the length of the subcategorization list for
lexical entries, even this expedient may be insufficient. In analyses
of Dutch cross-serial verb constructions [20,34]
subcategorization lists such as these may be appended by syntactic
rules
[59,90,68,103] resulting in indefinitely long lists.
Consider the Dutch sentence

The string of verbs is analyzed by appending their
subcategorization lists, as is illustrated in figure 3.7.
![\begin{figure}
\begin{center}
\leavevmode
\unitlength1pt
\beginpicture
\setplot...
...slaten}{release}}} [Bl] at 118.75 18.00
\endpicture
\end{center}\par\end{figure}](img214.png) |
In summary, top-down generation algorithms, even if controlled by the instantiation status of goals, can fail to terminate on certain grammars. The case given above, reminiscent of analyses from HPSG, as well as analyses from categorial unification grammar are examples in which the well-foundedness of the generation process resides in lexical information unavailable to top-down regimes. The conclusion of this section therefore is that top-down generators have problems with some linguistically motivated left recursive analyses. The source of the problem is that information available in lexical entries is not used sufficiently to guide the search.