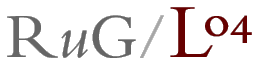
7. Voorbeeld: Duitsland
In dit deel maken we gebruik van een tabel van dialectverschillen voor
Duitsland, gebaseerd op data uit 186 plaatsen. [bron: Forschungsinstitut
für deutsche Sprache, Marburg?] De data zelf is niet
beschikbaar. De tabel en bestanden voor het tekenen van kaarten vind je in het
volgende zipbestand:
de.zip
In dit deel maken we kaarten met het programma
mapdiff. Met dit programma kun je een
kaart tekenen direct van een tabel met verschillen:
mapdiff -c 2 de.cfg de.dif > de00.ps
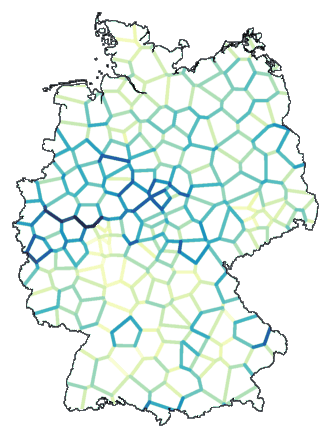
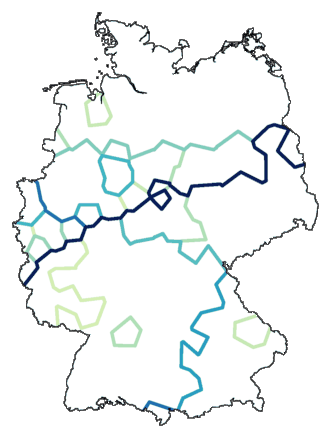
Hieronder zie je de kaart die dan ontstaat. De kleur van een lijn geeft aan
hoe groot het verschil tussen de plaatsen aan weerszijde van de lijn is. Hoe
donkerder de lijn des te groter het verschil.
Echt nuttig is zo'n kaart als hierboven niet. Je ziet alleen de lokale
verschillen, die op zich weinig zeggen. Het globale beeld ontbreekt.
Anders wordt het als je eerst gaat clusteren.
7.1 Van verschillen naar clusters naar verschillen
Als je gaat clusteren op basis van verschillen krijg je een indeling in
groepen. Die indeling in groepen zegt weer iets over de verschillen tussen
elementen, nu niet gebaseerd op individuele verschillen, maar gebaseerd op
verschillen tussen de groepen waar individuele elementen bij zijn ingedeeld.
Je begint simpel. Je maakt een clustering en verdeelt die in een aantal groepen. Uit die
groepsindeling maak je een nieuwe tabel met verschillen. Wanneer twee plaatsen
in dezelfde groep zijn ingedeeld dan is hun nieuwe verschil 0, en anders is het 1.
Met het programma cluster kun je clusteren,
en het resultaat direct omzetten in een nieuwe tabel met verschillen. Om
verschillen te krijgen op basis van een groepsindeling gebruik je de optie
-b. Met de optie
-m geef je aan op hoeveel groepen de verschillen
gebaseerd moeten worden. Hier een voorbeeld met een indeling in acht groepen:
cluster -wm -b -m 8 de.dif > tmp
mapdiff de.cfg tmp > de01.ps
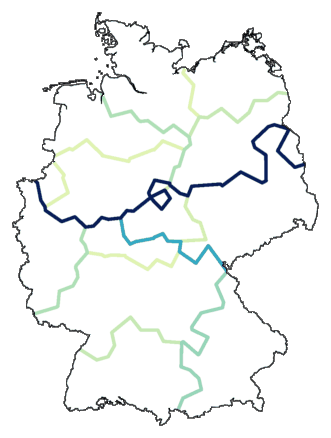
Met mapdiff zet je de nieuwe tabel van verschillen om
in een kaart, en het resultaat zie je hieronder:
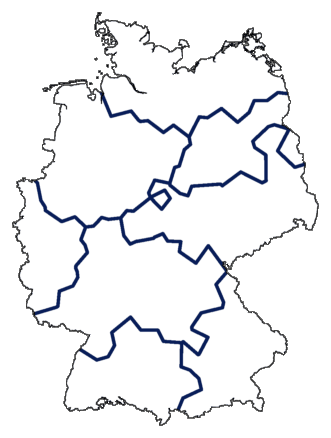
Dit ziet er uit als een gewone clusterkaart, waarbij clusters niet met kleuren,
maar met grenslijnen zijn aangegeven. Maar wanneer we het iets ingewikkelder
maken krijgen we veel meer te zien...
We clusteren, en maken een indeling in een aantal groepen. Liggen twee plaatsen
in dezelfde groep dan is hun verschil 0, anders is het 1. Dan maken we een
indeling in een ander aantal groepen. Liggen twee plaatsen dan in verschillende
groepen, dan wordt hun afstand met 1 verhoogd.
We beginnen met een indeling in twee groepen, dan in drie, steeds een
niveau verder, tot acht groepen:
cluster -wm -b -m 2-8 de.dif > tmp
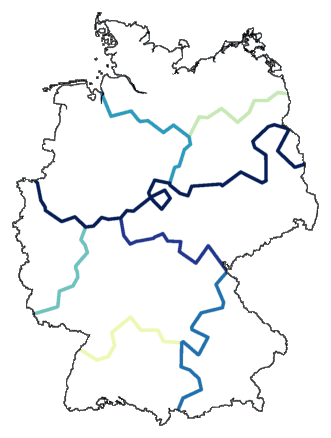
mapdiff -C .1 de.cfg tmp > de02.ps
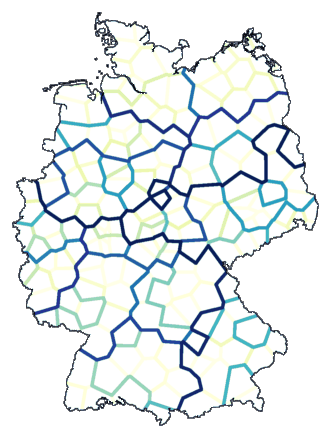
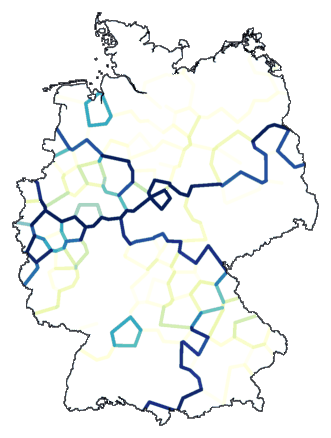
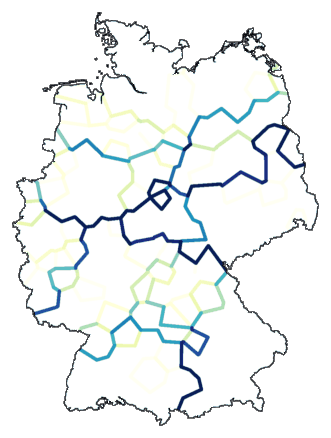
Het resultaat zie je hieronder. De donkerste lijn geeft de belangrijkste
opdeling aan, de iets lichtere lijn de volgende opdeling, enzovoort. Je krijgt niet een
"platte" indeling in clusters te zien, maar een stapsgewijze.
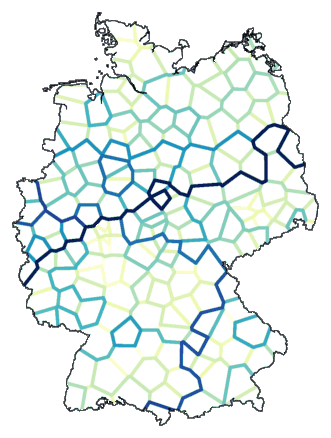
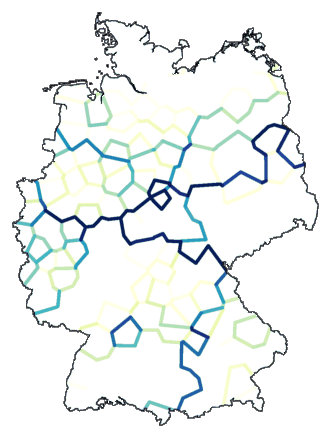
Waarom stoppen bij acht groepen? Er zijn 186 plaatsen. Laten we doorgaan met
opdelen tot aan die 186. (Om de lijnen redelijk zichtbaar te krijgen moet je
wat spelen met contrast, de opties
-c en
-C van
mapdiff.)
cluster -wm -b -m 2-186 de.dif > tmp
mapdiff -c 6 -C .1 de.cfg tmp > de03.ps
7.2 Cophenetic maps
Bij het clusteren worden groepen samengevoegd op basis van verschillen. In het
begin is elk element een cluster, een cluster met maar één element. De twee
clusters die onderling het kleinste verschil hebben worden samengevoegd tot een
nieuw cluster. Het verschil tussen dat nieuwe cluster, en elk van de
overgebleven clusters wordt berekend. (Hoe dat precies berekend wordt, dat
is wat de verschillende clustermethoden van elkaar onderscheidt.) Daarna worden
weer de twee clusters met het kleinste verschil samengevoegd. Enzovoort, tot
alles is samengevoegd in één groot cluster.
De afstanden tussen clusters (subclusters, subsubclusters) worden gebruikt
bij het tekenen van een dendrogram:
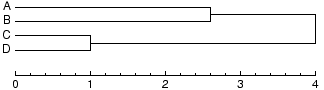
Die verschillen tussen clusters kunnen ook gebruikt worden als nieuwe verschillen
tussen elementen. Het verschil tussen twee elementen is dan het
verschil tussen de clusters die samengevoegd werden waarbij de twee
elementen samen in hetzelfde cluster terecht kwamen. Uit bovenstaand dendrogram
kun je zo de volgende tabel van verschillen afleiden:
| | | A | B | C | D
|
| | A | 0.0 | 2.6 | 4.0 | 4.0
|
| | B | 2.6 | 0.0 | 4.0 | 4.0
|
| | C | 4.0 | 4.0 | 0.0 | 1.0
|
| | D | 4.0 | 4.0 | 1.0 | 0.0
|
De verschillen in bovenstaande tabel worden de cophenetic
distances genoemd.
Met de optie -c kun je aangeven dat het programma
cluster een tabel van cofenetische
verschillen moet maken. Op basis van die tabel kun je een kaart tekenen. Een
voorbeeld, waarbij de clustermethode weighted average
wordt gebruikt:
cluster -wa -c de.dif > tmp
mapdiff -c 2 de.cfg tmp > de04.ps
Het wordt wat overzichtelijker als we een maximum aan het aantal groepen
stellen:
cluster -wa -c -m 24 de.dif > tmp
mapdiff -c 4 de.cfg tmp > de05.ps
Een ander voorbeeld, nu met de clustering volgens
Ward's method:
cluster -wm -c -m 12 de.dif > tmp
mapdiff -c .6 de.cfg tmp > de06.ps
7.3 Fuzzy clustering
Clustering, zoals we dat tot nu toe hebben gebruikt, heeft een belangrijke zwakheid:
het is instabiel. Kleine veranderingen (bijvoorbeeld ruis) in de oorspronkelijke meetgegevens kunnen soms
een groot effect hebben op de clustering, met name als het om clustergrenzen
gaat die in werkelijkheid helemaal niet zo duidelijk zijn als door een
gewone clusterkaart wordt gesuggereerd.
Die instabiliteit kunnen we benutten. We maken van een nadeel een voordeel.
Voordat we gaan clusteren voegen we zelf ruis toe aan de meetgegevens, en
kijken wat het effect is op de clustering. We doen dit niet een enkele keer, maar vele
malen. En dan tellen we hoe vaak een clustergrens getrokken wordt. Als we
daarvan een kaart tekenen dan geeft de kleur van de lijn aan hoe groot
de kans is dat een lijn daadwerkelijk deel is van een clustergrens.
Een voorbeeld, clustering volgens Ward's method, een indeling in acht groepen, ruisniveau 1,
de clustering vijftig keer herhaald:
cluster -wm -b -m 8 -N 1 -r 50 de.dif > tmp
mapdiff de.cfg tmp > de07.ps
Een ander voorbeeld, deze keer clustering met
weighted average en een indeling
in twaalf groepen:
cluster -wa -b -m 12 -N 1 -r 50 de.dif > tmp
mapdiff de.cfg tmp > de08.ps
Het programma
cluster kan maar één clustermethode
uitvoeren, en ook maar één tabel van verschillen gebruiken. Met het programma
difsum kun je tabellen samenvoegen, zodat
je toch kaarten kunt maken waarvoor meerdere clustermethoden gecombineerd
worden. In het volgende voorbeeld worden drie methoden gecombineerd. (Omdat de
eerste twee methoden sterk aan elkaar verwant zijn worden ze samen even zwaar
gewogen als de derde alleen.)
cluster -wa -b -m 12 -N 1 -r 50 de.dif > tmp-wa
cluster -ga -b -m 24 -N 1 -r 50 de.dif > tmp-ga
cluster -wm -b -m 8 -N 1 -r 50 de.dif > tmp-wm
difsum .5 tmp-wa .5 tmp-ga tmp-wm > tmp
mapdiff de.cfg tmp > de09.ps
7.4 Clustering en multidimensional scaling
We hebben al gezien dat clustering een afstandstabel omzet in een nieuwe
afstandstabel. Op die nieuwe afstandstabel kun je multidimensional scaling (MDS)
toepassen en daar een kleurenkaart van maken, net zoals bij de originele
afstandstabel, maar nu zie je het effect van de clustering in de kleurenkaart
terug. Met deze methode kun je clusters goed zichtbaar maken, zonder het nadeel
van een gewone clusterkaart, echter met nog wel wat nadelen die aan MDS kleven.
De kleurruimte is beperkt, en er kan dus ook maar een beperkt aantal clusters
worden weergegeven.
Uit tests met grote en kleine afstandstabellen onder uiteenlopende
omstandigheden kon een set parameters afgeleid worden waarmee in de
meeste gevallen een goed resultaat wordt verkregen:
- bepaling van cofenetische afstanden
- een combinatie van clustering met weighted average en group average
- ruis: ruisniveau 0,5 blijkt voldoende, 50 keer herhaald
- MDS volgens de klassieke methode
- gelijke weging voor alle kleurcomponenten bij het
tekenen van kaarten (maprgb met de optie -e)
Het laatste item heeft alleen duidelijk effect in zeer kleine gebieden, waar minder dan vier
"superclusters" zijn.
Met deze methode krijg je kaarten waarop clusters zijn ingedeeld in vier
hoofdkleuren, waarbinnen kleinere clusters worden aangegeven door variaties
binnen die hoofdkleuren.
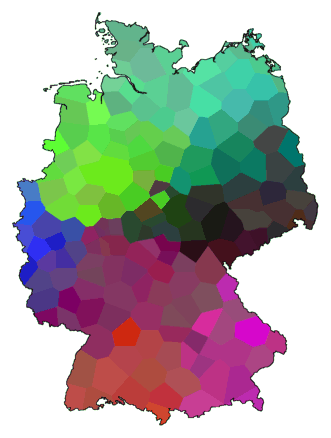
Hier volgt een voorbeeld waarbij de bovengenoemde parameters worden gebruikt:
cluster -wa -c -N .5 -r 50 de.dif > tmp1
cluster -ga -c -N .5 -r 50 de.dif > tmp2
difsum -a tmp1 tmp2 > tmp
mds 3 tmp > tmp.vec
maprgb -e de.cfg tmp.vec > de10.ps
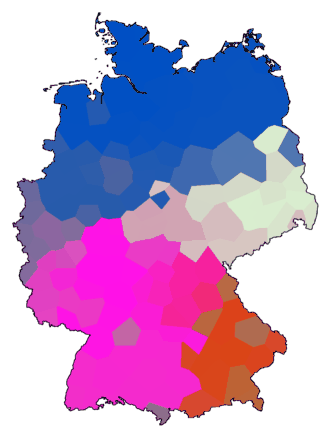
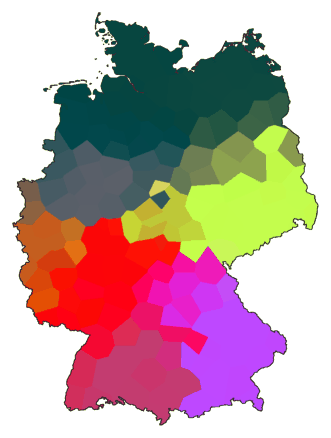
Hieronder volgen nog een aantal voorbeelden met andere parameters:
cluster -wm -b -m 8 de.dif > tmp1
difsum de.dif 4 tmp1 > tmp
mds -K 3 tmp > tmp.vec
maprgb de.cfg tmp.vec > de11.ps
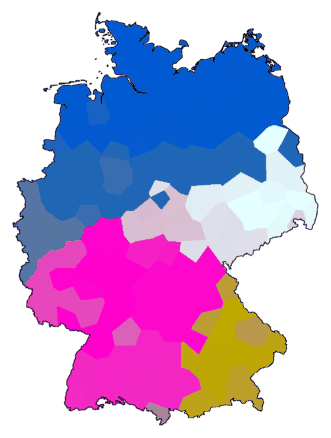
cluster -wm -b -m 8 -N 2 -r 100 de.dif > tmp
mds 3 tmp > tmp.vec
maprgb de.cfg tmp.vec > de12.ps
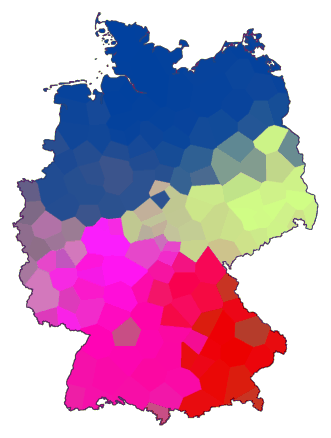
cluster -wa -c de.dif > tmp
mds 3 tmp > tmp.vec
maprgb de.cfg tmp.vec > de13.ps
cluster -wa -c -N 4 -r 100 de.dif > tmp
mds 3 tmp > tmp.vec
maprgb de.cfg tmp.vec > de14.ps
7.5 Vectorkaarten
Het gebruik van
mapdiff direct op de onbewerkte
afstandstabel is niet erg zinvol. Maar er is een manier om die onbewerkte
afstandstabellen wel direct in kaart te brengen, en dat is in de zogenaamde
vectorkaart, die je maakt met het programma
mapvec.
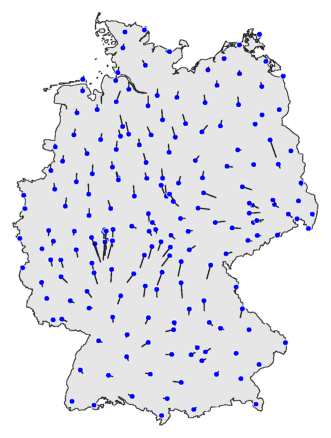
Direct hieronder zie je het commando waarmee je zo'n kaart maakt. Daaronder
links staat het resultaat. Om te verduidelijken hoe je zo'n vectorkaart moet
interpreteren staat ter vergelijking rechts een clusterkaart.
mapvec -n .2 de.cfg de.dif > de15.ps
De blauwe stippen zijn de plaatsen, de meetpunten. De zwarte streepjes zijn de
vectoren. Een vector wijst in de richting van het gebied met de
plaatsen waarmee het dialectverschil het kleinst is. Je
kunt dialectgrenzen herkennen doordat aan weerszijde van een grens de
vectoren van elkaar af wijzen.
Bij de bepaling van de vector van een plaats wordt alleen gekeken naar de
dialectafstand van die plaats met
andere plaatsen in de buurt. Alle plaatsen buiten het gebied worden genegeerd. De
grootte van die buurt kun je instellen met de optie
-n. Kies je een waarde dicht bij nul, dan is het
gebied erg klein. Kies je de waarde één, dan is het gebied gelijk aan
heel de kaart.
Het effect van verschillende waardes kun
je zien in deze animatie. Wanneer je een kleine
waarde kiest zie je meer lokale effecten, de niet zo belangrijke
dialectgrenzen. In de kaart hierboven kun je in het zuiden nog de dialectgrens
herkennen tussen het rode en het paarse gebied. Wanneer je de maximale waarde
kiest, dan verdwijnen de kleinere dialectgrenzen, en tekenen de
belangrijkste dialectgrenzen zich het duidelijkst af.