Home
Inleiding Informatiekunde: Opdracht 4
In de loop van de 90'er ging men over van de benoeming 'IT' naar wat
we vanddag 'ICT' noemen. Het besef was groot dat communicatie een
steeds belangrijkere rol speelt in het gebruik van
informatietechnologie. Een van de grootste (en beste)
computerfabricanten (SUN) adverteerde met de spreuk "het net is
de computer".
Inhoudelijke Richtlijnen
- De onzekerheid (entropie) wordt berekend als:
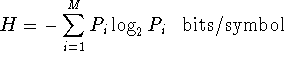 waar Pi de waarschijnlijkheid van de
symbool i (de ide symbool)
en M het aantal symbolen.
waar Pi de waarschijnlijkheid van de
symbool i (de ide symbool)
en M het aantal symbolen.
I.p.v. onzekerheid zou men ook het gem. niveau van
verassing kunnen zeggen. Let u op dat de
waarschijnlijkheden waarom het gaat steeds empirisch
vergaard moeten worden. Het is ondoenlijk om deze
a priori af te leiden.
- Claude Shannon gebruikte deze begrip van informationele
onzekerheid in de 50er jaren om communicatiesystemen te
ontwikkelen die zowel betrouwbaar waren als ook doelmatig.
- Een essentieel onderdeel van het begrip van Shannon is
dat men in het ontwerp van een informatie- en/of
communicatiesysteem rekening moet houden met de verdeling
van de boodschappen --- wat wordt het vaakst gezegd?
- Leg uit in hooguit 1,000 woorden het belang van dit
inzicht uit de informatietheorie voor werk in
geavanceerde communicatiesystemen. U mag voorbeelden
zoals de volgende in uw uiteenzetting gebruiken:
- Communicatie tussen mens en machine, b.v. de
"groene knop" op copiermachines (Suchman).
- Communicatie tussen mensen d.m.v. computers, zoals
dit geschiedt op web sites.
Veel organisaties laten hun web-sites hun
organisatiestructuur weerspiegel. Voor ieder
niveau in de organisatiestructuur is er een
menu keuze. Waarom staat dit haaks op het
inzicht van efficiënte codering zoals
Shannon dit formuleerde?
- Men probeert zich voor te stellen hoe de
bruikbaarheid van een text editor ontvangen zou worden
waar inderdaad "alles" kon, waar b.v. voor iedere letter
een aparte bepaling van grootte, oriëntatie, vorm,
en kleur nodig was.
Praktische Richtlijnen
Gebruik deze opdracht als kans om de onlangs geoefende vaardigheden
met BibTeX te oefenen.
- Gebruik LaTeX om de gelijking over entropie te laten zien.
Ja, dit betekent dat het mooiste is, als het ook in het
verhaal kan zijn. Als dat niet lukt, zet het gewoon in een
voetnoot aan het eind. Zie Wilkins' LaTeX
Primer, vooral de apragrafen over
Math mode,
superscripts and subscripts, en
standaard functies (sin, cos, etc.).
- Gebruik de grafiek in de bestand entropy.ps om het idee van de onzekerheid
(die in de informatietheorie ook "entropie" heet) te
verbeeldlijken. De grafiek toont de onzekerheid van een
variabele met maar twee mogelijkheden, b.v. het wel of
niet aanwezig zijn. Let op dat de grafiek maximaal is als
de kans precies 0,5 is -- dit is de situatie met de
maximale onzekerheid. Ze is minimaal waar de kans tegen 0 ofwel
1 gaan.
- Kleiweg geeft uitleg over hoe men grafieken in LaTeX
kan gebruiken in zijn Beginner's
LaTeX. Let u op wegen het gebruik van de regel
\usepackage{psfig}
- Gebruik een tweede grafiek die uzelf vindt b.v. op de
world-wide web. Deze moet u dan ook naar postscript
converteren, b.v. door middel van het programma xv.
Tips
Zie de eerste opdracht.
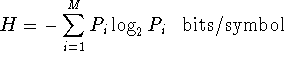 waar Pi de waarschijnlijkheid van de
symbool i (de ide symbool)
en M het aantal symbolen.
waar Pi de waarschijnlijkheid van de
symbool i (de ide symbool)
en M het aantal symbolen.