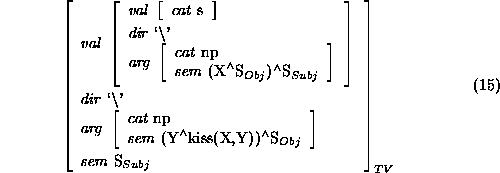

Next: Processing Up: Cross-Serial Dependencies Previous: Verb Clusters
The distribution and scope of adjuncts
The analysis of cross-serial dependencies in terms of argument inheritance interacts with the analysis of adjuncts presented in section 2.2. If a matrix verb inherits the arguments of the verb it governs, it should be possible to find modifiers of the matrix verb between this verb and one of its inherited arguments. This prediction is borne out (13a). However, we also find structurally similar examples in which the adjunct modifies the governed verb (13b). Finally, there are examples that are ambiguous between a wide and narrow scope reading (13c). We take it that the latter case is actually what needs to be accounted for, i.e. examples such as (13a) and (13b) are cases in which there is a strong preference for a wide and narrow scope reading, respectively, but we will remain silent about the (semantic) factors determining such preferences.
On the assumption that the lexical entries for lijken en ontwijken
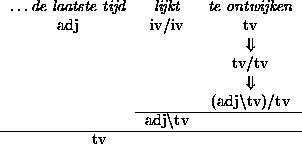
are as in (14), example (13c) has two possible derivations
(( ) and (
) and ( )). Procedurally speaking, the rule that adds
adjuncts can be applied either to the matrix verb (after division has taken
place) or to the governed verb. In the latter case, the adjunct is `inherited'
by the matrix verb. Assuming that adjuncts take scope over the verbs
introducing them, this accounts for the ambiguity observed above.
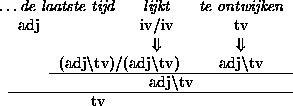
)). Procedurally speaking, the rule that adds
adjuncts can be applied either to the matrix verb (after division has taken
place) or to the governed verb. In the latter case, the adjunct is `inherited'
by the matrix verb. Assuming that adjuncts take scope over the verbs
introducing them, this accounts for the ambiguity observed above.
The assumption that adjuncts scope over the verbs introducing them can be
implemented as follows. We use a unification-based semantics in the spirit of
Pereira and Shieber [15]. Furthermore, the semantics is
head-driven, i.e. the semantics of a complex constituent is reetrant with
the semantics of its head (i.e. the functor). The feature structure for a
transitive verb including semantics (taking two NP's of the generalized
quantifier type 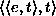 as argument and assigning
wide scope to the subject) is:
as argument and assigning
wide scope to the subject) is:
Thus, a lexical entry for a transitive verb can be defined as follows (where TV refers to the feature structure in 15):
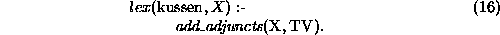
The lexical rule for adding adjuncts can now be extended with a semantics:
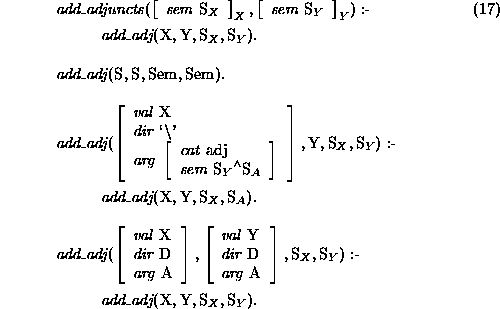
Each time an adjunct is added to the subcategorization frame of a verb, the
semantics of the adjunct is `applied' to the semantics as it has been built up
so far (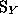 ), and the result (
), and the result (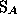 ) is passed on. The final
step in the recursion unifies the semantics that is constructed in this way with
the semantics of the `output' category. As an adjunct
) is passed on. The final
step in the recursion unifies the semantics that is constructed in this way with
the semantics of the `output' category. As an adjunct 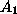 that appears to the
left of an adjunct
that appears to the
left of an adjunct 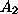 in the string will be added to the subcategorization
frame of the governing verb after
in the string will be added to the subcategorization
frame of the governing verb after 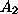 is added, this orders the (sentential)
scope of adjuncts according to left-to-right word order. Furthermore, since the
scope of adjuncts is now part of a verb's lexical semantics, any functor taking
such a verb as argument (e.g. verbs selecting for an infinitival complement)
will have the semantics of these adjuncts in its scope.
is added, this orders the (sentential)
scope of adjuncts according to left-to-right word order. Furthermore, since the
scope of adjuncts is now part of a verb's lexical semantics, any functor taking
such a verb as argument (e.g. verbs selecting for an infinitival complement)
will have the semantics of these adjuncts in its scope.
Note that the alternative treatments of adjuncts mentioned in section
2.2 cannot account for the distribution or scope of adjuncts in
cross-serial dependency constructions. Multiple (i.e. a finite number of)
categorizations cannot account for all possible word orders, since division
implies that a trigger for cross-serial word order may have any number of
arguments, and thus, that the number of `subcategorization frames' for such
verbs is not fixed. The polymorphic solution (assigning adjuncts the category
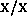 )
does account for word order, but cannot account for narrow
scope readings, as the adjunct will always modify the whole verb cluster (i.e
the matrix verb) and cannot be made to modify an embedded verb only.
)
does account for word order, but cannot account for narrow
scope readings, as the adjunct will always modify the whole verb cluster (i.e
the matrix verb) and cannot be made to modify an embedded verb only.


Next: Processing Up: Cross-Serial Dependencies Previous: Verb Clusters
Gertjan van Noord
Fri Nov 25 16:22:41 MET 1994