

Next: Morphology Up: Overview of the Previous: Overview of the
Reversible Unification Grammars
A unification grammar defined in grammar formalisms such as DCG [31] and PATR [42]
usually defines a relation between a string of words and some representation, sometimes
called logical form. In sign-based approaches such as UCG [55] and HPSG
[34], the string of words is not assigned a privileged status but is represented
as the value of one of the attributes of a feature structure.
In this approach a unification
grammar defines a set of feature structures where each feature structure represents a
pairing of a logical form and a string. Such a grammar
can thus be seen as defining two relations, a relation 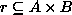 and
an its converse relation
and
an its converse relation 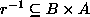 , where
, where 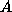 and
and 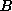 are, for example,
feature structures representing strings and feature structures representing logical forms.
Together these relations define the symmetric relation
are, for example,
feature structures representing strings and feature structures representing logical forms.
Together these relations define the symmetric relation 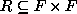 , where
, where
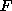 is the set of feature structures including
is the set of feature structures including 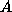 and
and 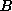 , and
, and 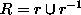 .
.
It is also possible to use unification grammars to define other symmetric relations between feature structures. In MiMo2 unification grammars are used to encode bilingual knowledge too: each (bilingual) unification grammar defines a symmetric transfer relation. Monolingual unification grammars define relations between strings and logical forms; bilingual grammars define relations between (language specific) logical forms.
In MiMo2 the translation relation between two natural languages is defined by a series of three unification grammars.
Each unification grammar defines
a symmetric relation, for example between Dutch strings and Dutch logical forms, or between
Dutch logical forms and English logical forms. Moreover each of these relations is
computable, and hence reversible. A relation
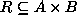 is called computable iff for a given
is called computable iff for a given 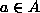 the
set
the
set 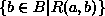 can be enumerated
by some terminating procedure. Although in general unification grammars are not computable
in this sense it is possible to constrain grammars to guarantee computability
[51][17][32]. We say that the composition
can be enumerated
by some terminating procedure. Although in general unification grammars are not computable
in this sense it is possible to constrain grammars to guarantee computability
[51][17][32]. We say that the composition 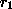

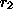 of two relations
of two relations 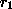 and
and 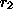 is {
is {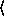 x,y
x,y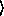 |
| 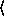 x,z
x,z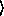
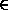
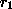 and
and 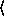 z,y
z,y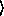
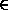
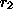 }.
It is easy to see that if
}.
It is easy to see that if 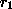 and
and 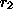 are both reversible (symmetric and computable),
are both reversible (symmetric and computable), 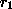

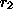 is also reversible.
is also reversible.
For example the relation 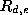 between Dutch and English strings is defined as the composition of the Dutch grammar in analysis direction, the Dutch-English bilingual grammar in the Dutch-to-English direction, and the English grammar in generation direction. Each translation relation that can be defined in MiMo2 is thus necessarily reversible.
between Dutch and English strings is defined as the composition of the Dutch grammar in analysis direction, the Dutch-English bilingual grammar in the Dutch-to-English direction, and the English grammar in generation direction. Each translation relation that can be defined in MiMo2 is thus necessarily reversible.


Next: Morphology Up: Overview of the Previous: Overview of the
Gertjan van Noord
Thu Nov 24 19:09:23 MET 1994