Per subset and per state

The per subset and the per state algorithms use a simplified variant of the transitive closure algorithm for graphs. Instead of computing the transitive closure of a given graph, this algorithm only computes the closure for a given set of states. Such an algorithm is given in figure 4.

Figure 4: Epsilon-closure Algorithm

$\begin{program} \FUNCT \vert closure\vert(T) D := \emptyset \FOREACH t\in T \DO ... ...d } q \mbox{ unmarked to } D \FI \OD \OD \keyword{return} ~D \END \end{program}$

In both of the two integrated approaches, the subset construction algorithm is initialised with an agenda containing a single subset which is the $\epsilon$ -CLOSURE of the set of start-states of the input; furthermore, the way in which new transitions are computed also takes the effect of $\epsilon$ -moves into account. Both differences are accounted for by an alternative definition of the epsilon_closure function.

The approach in which the transitive closure is computed for one state at a time is defined by the following definition of the epsilon_closure function. Note that we make sure that the transitive closure computation is only performed once for each input state, by memorising the closure function; the full computation is memorised as well. ⁴

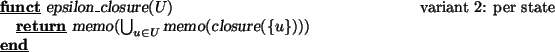
$\begin{program} \FUNCT \vert epsilon_closure\vert(U) \rcomment{variant 2: per st... ...t(\bigcup_{u\in U}\vert memo\vert(\vert closure\vert(\{u\}))) \END \end{program}$

In the case of the per subset approach, the closure algorithm is applied to each subset. We also memorise the closure function, in order to ensure that the closure computation is performed only once for each subset. This can be useful since the same subset can be generated many times during subset construction. The definition simply is:

$\begin{program} \FUNCT \vert epsilon_closure\vert(U) \rcomment{variant 3: per subset} \keyword{return}~ \vert memo\vert(\vert closure\vert(U)) \END \end{program}$

The motivation for the per state variant is the insight that in this case the closure algorithm is called at most |Q| times. In contrast, in the per subset approach the transitive closure algorithm may need to be called 2^|Q| times. On the other hand, in the per state approach some overhead must be accepted for computing the union of the results for each state. Moreover, in practice the number of subsets is often much smaller than 2^|Q|. In some cases, the number of reachable subsets is smaller than the number of states encountered in those subsets.