Next: Avoiding Overgeneration Up: A lexicalist account of Previous: Implementing Polymorphism

Extending Coverage

The definition of division presented in the previous section only allows for disharmonic division of right-directional functors. To account for inverted word orders within the verb cluster, other instances of division are also needed.

Finite modals as well as auxiliaries allow for inversion in the verb cluster, that is, the governed verb may occur to their left, rather than to the right:

$\eenumsentence{ \item[a.]\shortex{5}{\ldots dat &Jan &een brief &schrijven &wil}... ...t} {\ldots that&John&Mary&kissed&has} {\em\ldots that John has kissed Mary} }$

Verb clusters with inverted word order may seperate a head from its argument, if that head selects for an argument to the right:

$\enumsentence{ \shortex{7} {\ldots dat &Jan&geleerd &heeft &zich &aan &te passen... ...self& {\sc prt} &to adapt} {\em\ldots that John has learned to adapt himself} }$

To account for inversion we assume that an auxiliary such as hebben is assigned an initial category VP\VP and that it is subject to division. Note, however, that since governors inducing inverted word order are left-directional, a leftward version of disharmonic division is needed to derive examples such as (11) (in (13) and below we use A $\Rightarrow$ B to represent an instance of division):

$\enumsentence{ $Y\backslash X \rightarrow (Y/Z)\backslash(X/Z)$\ \hspace{2cm} {\bf Leftward Disharmonic Division} }$

$\enumsentence{ \sc \begin{tabular}[t]{rcccc} \ldots & {\em Jan}&{\em geleerd} & ... ...olumn{2}{c}{vp$/$vp} \\ \cline{4-5} &&& \multicolumn{2}{c}{vp} \end{tabular}}$

Next, consider cases in which the governed verb is an extraposition verb selecting an NP-object:

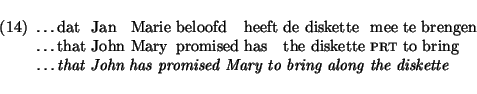
$\enumsentence{ \shortex{8} {\ldots dat & Jan & Marie & beloofd& heeft & de diske... ...to bring} {\em\ldots that John has promised Mary to bring along the diskette} }$

The category of beloven is (NP\VP)/VP. This implies that the auxiliary can only combine with the preceding participle if it can undergo leftward harmonic (15) as well as disharmonic division:

$\enumsentence{ $Y\backslash X \rightarrow (Z\backslash Y)\backslash (Z\backslash X)$\ \hspace{2cm} {\bf Leftward Harmonic Division} }$

$\enumsentence{\sc \begin{tabular}[t]{rc@{\hspace{1cm}}ccc} \ldots & {\em beloofd... ...)$/$vp} \\ \cline{3-5} && \multicolumn{3}{c}{np$\backslash$vp} \end{tabular}}$

For modal verbs, inversion is possible only if the modal is finite. For auxiliaries, however, inversion is also possible if the auxiliary is non-finite:

$\enumsentence{ \shortex{8} {\ldots dat & Jan & geleerd & moet & hebben & zich & ... ...\sc prt} & to adapt} {\em\ldots that John must have learned to adapt himself} }$

Note that in these cases the participle does not occur left-adjacent to the auxiliary, but at the left-periphery of the verb-cluster. Assuming that hebben is assigned the category (VP/VP)\(VP/VP) (as in (13)), a derivation of (17) is possible only if the VR verb moet can undergo rightward harmonic division:

$\enumsentence{ $X/Y \rightarrow (X/Z)/(Y/Z)$\ \hspace{2cm} {\bf Rightward Harmonic Division} }$

$\enumsentence{\sc \begin{tabular}[t]{rcccc} \ldots & {\em geleerd} & {\em moet} ... ...ash($vp$/$vp)} \\ \cline{2-3} & \multicolumn{2}{c}{vp$/$vp} \\ \end{tabular}}$

The upshot of the discussion in this section is that leftward and rightward, disharmonic as well as harmonic, division is needed to account for the word order posibilities within the verb cluster. Note that all four instances of division can be captured in a unification-based setting by generalizing the previous definition in (9) as shown in (20). From now on, we assume that VR and PE verbs are subject to this general constraint.

$\enumsentence{ $ \begin{array}[t]{l} \mbox{\it division}(\var{In},\var{In}). \\ ... ... } \var{X}\\ \att{dir } \var[2]{D} \\ \att{arg } \var{Y} }). \end{array}$}$

Next: Avoiding Overgeneration Up: A lexicalist account of Previous: Implementing Polymorphism

Noord G.J.M. van
1998-09-29