


Next: Symmetry Up: Reversible Unification Grammars Previous: Reversible Unification Grammars
Reversibility
I will call a binary relation
reversible
if the relation is symmetric and computable. Both symmetry and computability
will be explained in the following subsections.
A grammar 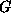 is reversible for a relation
is reversible for a relation 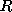 iff
iff 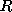 is reversible and defined by
is reversible and defined by 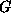 .
For example, a grammar that relates strings to logical forms is reversible if both the parsing
and generation problem is computable, and the relation between strings and
logical forms is symmetric; the parsing problem is computable if for a given string
all corresponding logical forms can be enumerated by some terminating procedure;
such a procedure should halt if the given string does not have a corresponding
logical form.
Thus: reversible = symmetric + computable. Note that reversibility as defined here
is different from bidirectionality. The latter merely says that grammars are to be
used in two directions, but does not state how the two directions relate.
.
For example, a grammar that relates strings to logical forms is reversible if both the parsing
and generation problem is computable, and the relation between strings and
logical forms is symmetric; the parsing problem is computable if for a given string
all corresponding logical forms can be enumerated by some terminating procedure;
such a procedure should halt if the given string does not have a corresponding
logical form.
Thus: reversible = symmetric + computable. Note that reversibility as defined here
is different from bidirectionality. The latter merely says that grammars are to be
used in two directions, but does not state how the two directions relate.
It is easy to see that a composition of reversible relations is a a reversible relation
too; i.e. if some feature structure 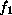 is related to some
feature structure
is related to some
feature structure 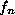 via the reversible relations
via the reversible relations 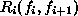 , each defined by some
reversible grammar
, each defined by some
reversible grammar 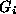 , then
, then 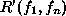 is reversible.
Thus an MT system that defines a relation
is reversible.
Thus an MT system that defines a relation 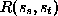 via the relations
via the relations
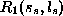 ,
, 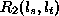 and
and 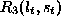 is reversible if
is reversible if 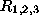 are reversible.
are reversible.
Gertjan van Noord
Fri Nov 25 13:42:02 MET 1994