Next: Possible relaxations Up: Reversibility Previous: Symmetry
Computability
A relation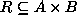 
is computable iff for a given 
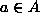the
set 
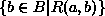can be enumerated
by some terminating procedure.
To discuss computability it is useful to look a bit more careful at the
relations we are interested in. These relations are all binary relations between
feature structures. However, in the case of the relation between strings and
logical forms, strings will always be related to logical forms and logical forms
will be related to strings.
Similarly for the relation between Dutch and Spanish logical forms.
Clearly, the domain and range of the relation is
structured and can be partioned into two sets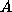 
and 
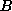, for example the set of
feature structures representing strings and the set of feature structures
representing logical forms.
The relation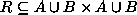 
can be partitioned similarly into the
relations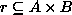 
and its inverse, 
.
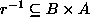The problem to compute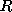 
is now replaced by two problems: the computation
of 
and 
.
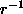For example the problem to compute the relation between logical forms and strings
consists of the parsing- and generation problem.
It is now possible to incorporate the notion of equivalence, to
obtain a definition of a parser, generator and translator. For example, an
algorithm that computes the foregoing relation will enumerate for a given
features structure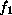 
all feature structures 
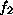, such that 
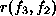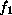and
and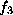 
are equivalent. In the case of strong equivalence this implies
that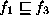 
(completeness), and 
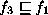(coherence).
In other words, the input should not be extended (coherence) and should completely
be derived (completeness). This usage of the terms completeness and coherence was
introduced in [24].
In the following I will discuss ways to obtain computability of one such partition.
It is well known that relations defined by unrestricted unification grammars are not computable in general as such grammars have Turing power [13]; it is thus not decidable whether the relation is defined for some given input. Usually some constraint on grammars is defined to remedy this. For example the off-line-parsability constraint [5][13] ensures that the recognition problem is solvable. Moreover this constraint also implies that the parsing problem as defined here is computable; i.e. the proof procedure will always terminate (because the constraint implies that there is a limit to the depth of possible parse trees for all strings of a given length).
However the off-line-parsability constraint assumes a context-free base of the formalism. A generalization of the off-line-parsability constraint for any binary relation defined by unification grammars will consist of three parts; the first and third of these parts are usually implicit in the case of parsing.
First, the value of the input must be built in a well-behaved compositional way. For example in the case
of parsing:
each daughter of a rule dominates part of the string dominated by
the mother of that rule. Similarly for transfer and generation: each daughter of a rule has
a value for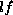 
that is part of the value of 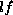of the mother.
Second, a special condition is defined for rules where the input value of the mother is the same as the input value of one of the daughters. For parsing such rules have exactly one daughter. A chain of applications of such rules is disallowed by some constraint or other; this is the core of most definitions of the off-line parsability constraint. For example in [13] such a chain is disallowed as the principal functor of a term may only occur once in a chain. For a slightly more general definition, cf. [5]. For generation and transfer a similar constraint can be defined. In the terminology of [19][18] the `head' of a rule is a daughter with the same logical form as its mother. A chain of these heads must be disallowed.
Third, the input should not get extended during the proof procedure.
In the case of parsing this is achieved easily because the input is ground 
.
For generation and transfer this
is not necessarily the case. This is the point where the usefulness of the coherence condition
comes in; the coherence requirement explicitly states that extension
of the input is not allowed.
For this reason strong reversiblity may be easier to obtain than weak reversibility.
In the next subsection I will discuss two relaxations of strong symmetry that will not
affect the computability properties discussed here.
Generalizing the terminology introduced by [13] a proof procedure is strongly stable iff it always terminates for grammars that adhere to a generalized off-line parsability constraint. In [15] a general proof procedure for DCG based on head-driven generation [22][19][18] is defined that is strongly stable for a specific instantiation of the generalized off-line parsability constraint.
Next: Possible relaxations Up: Reversibility Previous: Symmetry
Gertjan van Noord
Fri Nov 25 13:42:02 MET 1994