Lexical Rules as Constraints on Lexical Categories

Rather than formalizing the `add-adjuncts' rule as a lexical rule we propose to use recursive constraints on lexical categories. Such lexical constraints are then processed using delayed evaluation techniques. ³

Such an approach is more promising than an off-line approach that precomputes the effect of lexical rules by compilation of the lexicon, as it is unclear how recursive lexical rules can be treated in such an architecture (especially since some recursive rules can easily lead to an infinite number of lexical entries, e.g. the adjuncts rule).

Another alternative is to consider lexical rules as `ordinary' unary rules. If this technique is applied for the lexical rules we have envisaged here, then (unary) derivations with unbounded length have to be considered.

If we formalize lexical rules as (complex) constraints on lexical categories then we are able to use delayed evaluation techniques for such constraints.

Assume that the `underlying' feature structure of a verb is given by a definition of `stem' (e.g. as the example of `wil' above, or as the example of a simple transitive verb such as `kussen' (to-kiss) in figure 6).

**Figure 6:** Category for `kussen' (to kiss)
$\begin{figure}\begin{center}$ \avm{\mbox{\sc verbal}\\ \mbox{\it sc}: \langle\... ...isser}: \mbox{A}_1\\ \mbox{\it kissed}: \mbox{A}_2}} $\end{center}\end{figure}$

Such a feature-structure is not the actual category of the verb -- rather this category is defined with complex constraints with respect to this base form. Here the constraint that adds adjuncts to the subcat list has our special attention, but there is also a constraint that adds a subject to the subcat list (as part of the inflection constraint for finite verbs) and a constraint that pushes an element from the subcat list to slash (to treat unbounded dependencies along the lines of chapter 9 of [7]), etc. Thus a lexical entry might be defined as in figure 7.

**Figure 7:** A lexical entry is defined with respect to a base form using complex constraints. Subject addition is a constraint associated with finite inflection.
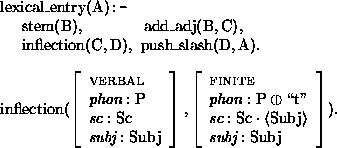$\begin{figure} \begin{flushleft} $\mbox{lexical\_entry} (\mbox{A}){\mbox{\tt :-}... ...ubj}\rangle \\ \mbox{\it subj}: \mbox{Subj}}).$\\ \end{flushleft}\end{figure}$

Lexical rules are regarded as (complex) constraints in this framework because it allows an implementation using delayed evaluation techniques from logic programming. The idea is that a certain constraint is only (partially) evaluated if `enough' information is available to do so successfully. As a relatively simple example we consider the constraint that is responsible for adding a subject as the last element on a subcat list of finite verbs. As a lexical rule we might define:

$\begin{figure} \begin{center} $ \avm{\mbox{\sc finite}\\ \mbox{\it subj}: \mbo... ...mbox{\it sc}: \mbox{Sc}\cdot\langle\mbox{Subj}\rangle} $\end{center}\end{figure}$

If we use constraints the definition can be given as in figure 7, as part of the constraint associated with finite morphology. Note that the two approaches are not equivalent. If we use lexical rules then we have to make sure that the add-subject rule should be applied only once, and only for finite verbs. As a constraint we simply call the constraint once at the appropriate position.

The concatenation constraint (associated with the `dot' notation) is defined as usual:

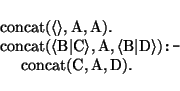
$\begin{flushleft} $ \mbox{concat} (\langle\rangle,\mbox{A},\mbox{A}).$\\ $ \m... ...:-}}$\\ $ ~~~~ \mbox{concat} (\mbox{C},\mbox{A},\mbox{D}). $\\ \end{flushleft}$
If this constraint applies on a category of which the subcat list is not yet fully specified (for example because we do not yet know how many adjuncts have been added to this list) then we cannot yet compute the resulting subcat list. The constraint can be successfully applied if either one of the subcat lists is instantiated: then we obtain a finite number of possible solutions to the constraint.

The relation add_adj recursively descends through a subcategorization list and at each position either adds or does not add an adjunct (of the appropriate type). Its definition is given in figure 8.

**Figure 8:** Definite clause specification of `add_adj' constraint.
$\begin{figure} \begin{flushleft} $ \mbox{add\_adj} (\avm{ \mbox{\sc sign} \\ ... ...dd\_adj} (\mbox{A},\mbox{D},\mbox{E},\mbox{C}). $\\ \end{flushleft}\end{figure}$