



Next: Definite clauses of ()
Up: A Powerful Grammar Formalism
Previous: Determining satisfiability
Adding definite relations
In this section I will apply the construction defined by
[32] to the constraint language defined in the
preceding section to obtain
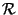 (
(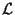 ). It is shown in
[32] how the nice properties of logic
programming languages carry over to a whole class of formalisms built
on top of arbitrary constraint languages. The idea is to distinguish
between the underlying constraint language (for example
). It is shown in
[32] how the nice properties of logic
programming languages carry over to a whole class of formalisms built
on top of arbitrary constraint languages. The idea is to distinguish
between the underlying constraint language (for example 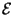 ,
where
,
where 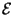 consists of conjunctions of equations between
first-order terms) and the definite relations that are defined using
constraints from the underlying constraint language. In the case of
consists of conjunctions of equations between
first-order terms) and the definite relations that are defined using
constraints from the underlying constraint language. In the case of
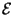 this results in
this results in
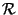 (
(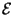 ), which is just first-order
logic. From the resulting logic we then take definite clauses,
and in the case of
), which is just first-order
logic. From the resulting logic we then take definite clauses,
and in the case of 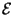 we thus end up with (pure) Prolog. The
constraint language
we thus end up with (pure) Prolog. The
constraint language 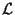 can be seen as another instance of such
a constraint language. To this constraint language I apply the
construction sketched above, resulting in
can be seen as another instance of such
a constraint language. To this constraint language I apply the
construction sketched above, resulting in
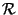 (
(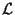 );
);
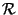 (
(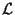 ) is thus
rather similar to pure Prolog, but equations between first order terms
are replaced by the path equations introduced in the previous section.
Instead of first order terms, our data structures are feature
structures. Furthermore, unlike PATR II I will not restrict the
formalism by requiring that phrases are built by concatenation.
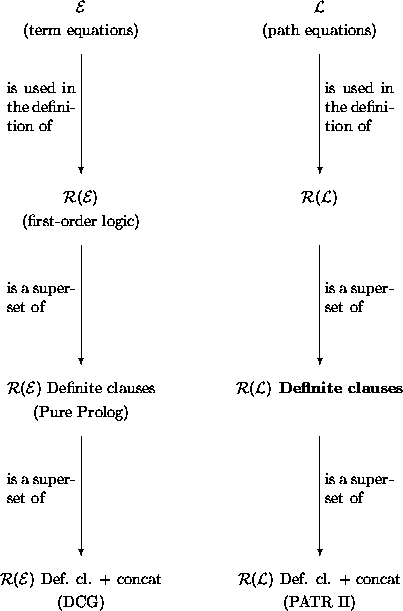
In figure 2.3 it is shown how the different
formalisms are related.
) is thus
rather similar to pure Prolog, but equations between first order terms
are replaced by the path equations introduced in the previous section.
Instead of first order terms, our data structures are feature
structures. Furthermore, unlike PATR II I will not restrict the
formalism by requiring that phrases are built by concatenation.
In figure 2.3 it is shown how the different
formalisms are related.
Figure 2.3:
Overview of the different formalisms
 |




Next: Definite clauses of ()
Up: A Powerful Grammar Formalism
Previous: Determining satisfiability
Noord G.J.M. van
1998-09-30
