Next: Marking a derivation Up: A monitoring strategy Previous: Ambiguities are often
Locating ambiguity with derivation trees.
We hypothesise that a good way to characterise the location of the ambiguity of an utterance is by referring to the notion of `derivation tree'. We are assuming that the underlying grammar formalism comes with a notion `derivation tree' which represents how a certain derivation is licenced by the rules and lexical entries of the grammar. Note that such a derivation tree does not necessarily reflect how the parser or generator goes about finding such a derivation tree for a given string or logical form. For example, the derivation trees of the two readings of `john is standing near the bank' may look as in figure 1. The intuition that the ambiguity of this sentence is local is reflected in these derivation trees: the trees are identical up to the difference between bank4 and bank7. In our examples each sign sign(LF,Str,Syn,D) is specified for its corresponding derivation tree D. In Prolog such a tree is represented with terms of the form t(Label,Ds,M) where Label is the node name (the unique name of a rule) and Ds is a list of Daughter trees. The third argument position will be explained below.
Given a derivation tree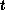 
of a generated sentence 
, we
mark the places where the ambiguity occurs as follows. If is
ambiguous it can be parsed in several ways, giving rise to a set of
derivation trees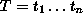 
. We now compare 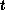with the
set of trees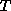 
in a top-down fashion. If for a given node label in
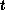there are several possible labels at the corresponding nodes in
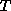then we have found an ambiguous spot, and the corresponding node
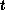in is marked. Thus, in the previous example of structural
ambiguity we may first generate sentence (2) above. After
checking whether this sentence is ambiguous we obtain, as a result,
the marked derivation tree of that sentence. A marked node in such a
tree relates to an ambiguity. The relevant part of the resulting
derivation tree of the example above may be the tree in
figure 2.
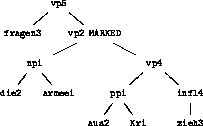
Figure 2: Marked derivation tree
Next: Marking a derivation Up: A monitoring strategy Previous: Ambiguities are often
Gertjan van Noord
Thu Nov 24 18:08:35 MET 1994