Succintness

Predicate-augmented finite state transducers typically require fewer transitions than classical finite state transducers, by an argument similar to that for pfsr. In the case of predicate-augmented pfst with bounded queue, however, the number of states can often be much smaller than the number of states in an equivalent, classical, sub-sequential transducer. Consider again the first example in section 3.4. Application of our variant of Mohri's determinization algorithm yields a transducer of 5 states and 5 transitions, repeated here for convenience:

Figure 1: A minimal subsequential transducer without predicates. The equivalent minimal transducer employing predicates only has 5 states and 5 transitions.

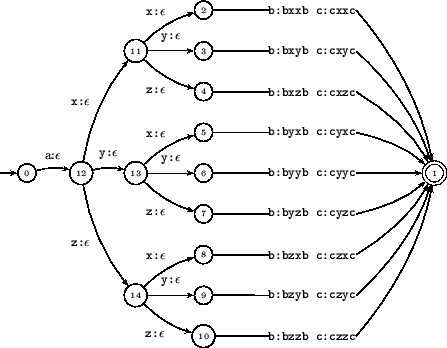
Suppose we were to expand this example into a classical subsequential transducer, then depending on the size of the alphabet, the resulting transducers would have many more states. The example for the alphabet $\{\mbox{\tt x,y,z}\}$ with 15 states and 31 transitions is given in figure 1; for an alphabet of 26 symbols, the result already has 705 states and 2055 transitions. For an alphabet of 254 symbols, the result has 64773 states and 193803 transitions. Instead of having two question marks on the input side in a row, consider similar examples where we have k such question marks in a row:

In these cases, the minimal qpfst will have 3+k states. The equivalent minimal subsequential transducer will require $3 + \vert\Sigma\vert + \vert\Sigma\vert^2 + \dots + \vert\Sigma\vert^k$ states. An analysis of the difference in succintness in terms of descriptional complexity (e.g. [7]) is beyond the scope of this article; but this class of examples suggests that there are arbitrarily many relations for which the qpfst device requires exponentially fewer states than subsequential transducers.