Solutions of constraints

An interpretation $\cal {I}$ of $\cal {L}$ consists of a domain D^{$\cal {I}$} which is the set of all feature graphs built from L, C and V, and a solution mapping ^{. $\cal {I}$} which will be defined below. An $\cal {I}$-assignment is a mapping from the set of variables to D^{$\cal {I}$}. I write ASS^{$\cal {I}$} for the set of all $\cal {I}$-assignments. Variables and constants will denote feature graphs, relative to some assignment.

The denotation of a variable X w.r.t. assignment $\alpha$ is simply $\alpha$(X). The denotation of a constant c is the feature graph (c,$\emptyset$) (for any assignment). The denotation of a descriptor sp is defined as F^p where F is the denotation of s; i.e. the denotation of sp is the subgraph at p of the graph denoted by s. Note that the denotation of some descriptors is undefined. Summarizing:

$$\begin{array}{l} \mbox{\rm c}_{\alpha}^{\cal{I}} =_{def} (\m... ...sp)^{\cal{I}}_\alpha =_{def} (s^{\cal{I}}_\alpha)^p \end{array}$$

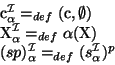
As an example, consider the feature graph F₂ in figure 2.2.

Figure 2.2: The feature graph F₂

For an assignment that maps X to the feature graph F₂, the denotation of the descriptor Xl₁l₃ is the subgraph rooted at X₂. Similarly, the denotation of Xl₂l₄l₂ is the feature graph (c₃,$\emptyset$). Note that the denotation of the descriptor c (i.e. c$\epsilon$) is the feature graph (c,$\emptyset$).

An interpretation $\cal {I}$ satisfies an atomic constraint $\phi$ = d₁ $\doteq$ d₂, relative to an assignment $\alpha$, written $\cal {I}$ $\models_{\alpha}^{}$ $\phi$ if the denotation of descriptors d₁, d₂ are both defined and the same, i.e.:

$${\cal{I}} \models_\alpha d_1 \doteq d_2\mbox{ iff }(d_1)^{\cal{I}}_\alpha = (d_2)^{\cal{I}}_\alpha$$
Hence, $\cal {I}$ satisfies the equation Xl₁l₃ $\doteq$ Xl₂l₃ with respect to the assignment that maps X to the feature graph F₂ defined above. As another example, $\cal {I}$ also satisfies the equation Xl₁l₃l₁ $\doteq$ c₂, with the same $\alpha$.

The solutions of a constraint are all assignments that give satisfaction. Constraints are thus seen as restrictions on the values the variables in the constraints can take. The solutions of an atomic constraint $\phi$ are defined as follows:

$$\phi^{\cal{I}} =_{def} \{ \alpha \in ASS^{\cal{I}} \vert \cal{I} \models_\alpha \phi \}$$
The set of solutions of a constraint $\phi_{1}^{}$,...,$\phi_{n}^{}$ is defined as the intersection of the solutions of its atomic constraints:

($$\phi_{1}^{}$$,...$$\phi_{n}^{}$$)^{$\cal {I}$} = _def$$\bigcap_{1 \leq i \leq n}^{}$$$$\phi_{i}^{\cal{I}}$$

A constraint is satisfiable iff it has at least one solution. Two constraints are equivalent iff they have the same solutions. A constraint is valid iff its solutions are all possible assignments ASS^{$\cal {I}$}.