

Introduction to mixed-effects regression for (psycho)linguists
Lecture 1 of advanced regression for linguists
Martijn Wieling
Computational Linguistics Research Group
Course setup (1)
- Five sessions (2 - 3 hours each):
- Mon. Jan. 23, 10 AM - 1 PM: Intro to mixed-effects regression with reaction time data
- Tue. Jan. 24, 10 AM - 1 PM: Generalized mixed-effects regression and eye-tracking data
- Mon. Jan. 30, 10 AM - 1 PM: Intro to generalized additive modeling with articulography data
- Wed. Feb. 1, 10 AM - 1 PM: Generalized additive modeling with EEG data
- Thu. Feb. 2, 10 AM - 1 PM: Generalized additive logistic modeling with dialect data
Course setup (2)
- User-centered, so each lecture:
- Part I: introductory lecture (max. 90 minutes)
- Short break
- Part II: hands-on lab session (max. 90 minutes)
- You probably won't be able to finish all exercises from the lab session during the lecture
- To get the most out of the course, try to finish them by yourself (additional information is present in the lab sessions)
- Questions: ask immediately when something is unclear!
This lecture
- Introduction
- Recap: multiple regression
- Mixed-effects regression analysis: explanation
- Methodological issues
- Case-study: Lexical decision latencies (Baayen, 2008: 7.5.1)
- Conclusion
Introduction
- Consider the following situation (taken from Clark, 1973):
- Mr. A and Mrs. B study reading latencies of verbs and nouns
- Each randomly selects 20 words and tests 50 participants
- Mr. A finds (using a sign test) verbs to have faster responses
- Mrs. B finds nouns to have faster responses
- How is this possible?
The language-as-fixed-effect fallacy
- The problem is that Mr. A and Mrs. B disregard the variability in the words (which is huge)
- Mr. A included a difficult noun, but Mrs. B included a difficult verb
- Their set of words does not constitute the complete population of nouns and verbs, therefore their results are limited to their words
- This is known as the language-as-fixed-effect fallacy (LAFEF)
- Fixed-effect factors have repeatable and a small number of levels
- Word is a random-effect factor (a non-repeatable random sample from a larger population)
Why linguists are not always good statisticians
- LAFEF occurs frequently in linguistic research until the 1970's
- Many reported significant results are wrong (the method is anti-conservative)!
- Clark (1973) combined a by-subject (\(F_1\)) analysis and by-item (\(F_2\)) analysis in measure min F'
- Results are significant and generalizable across subjects and items when min F' is significant
- Unfortunately many researchers (>50%!) incorrectly interpreted this study and may report wrong results (Raaijmakers et al., 1999)
- E.g., they only use \(F_1\) and \(F_2\) and not min F' or they use \(F_2\) while unneccesary (e.g., counterbalanced design)
Our problems solved...
- Apparently, analyzing this type of data is difficult...
- Fortunately, using mixed-effects regression models solves these problems!
- The method is easier than using the approach of Clark (1973)
- Results can be generalized across subjects and items
- Mixed-effects models are robust to missing data (Baayen, 2008, p. 266)
- We can easily test if it is necessary to treat item as a random effect
- But first some words about regression...
Regression vs. ANOVA (1)
- Most people either use ANOVA or regression
- ANOVA: categorical predictor variables
- Regression: continuous predictor variables
- Both can be used for the same thing!
- ANCOVA: continuous and categorical predictors
- Regression: categorical (dummy coding) and continuous predictors
Regression vs. ANOVA (2)
- Why I use regression as opposed to ANOVA
- No temptation to dichotomize continuous predictors
- Intuitive interpretation (your mileage may vary)
- Mixed-effects analysis is relatively easy to do and does not require a balanced design (which is generally necessary for repeated-measures ANOVA)
- This course will focus on regression
Recap: multiple regression (1)
- Multiple regression: predict one numerical variable on the basis of other independent variables (numerical or categorical)
- (logistic regression is used to predict a binary dependent variable)
- We can write a regression formula as \(y = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \epsilon\)
- \(y\): (value of the) dependent variable
- \(x_i\): (value of the) predictor
- \(\beta_0\): intercept, where the regression line crosses the \(y\)-axis (i.e. value of \(y\) when all \(x_i = 0\))
- \(\beta_i\): change of the dependent variable when the predictor value increases with 1 (i.e. slope)
- \(\epsilon\): residuals (difference between observed values and predicted values)
Recap: multiple regression (2)
- Example of regression formula:
- Predict the reaction time of a participant on the basis of word frequency, word length, and subject age: RT = 200 - 5WF + 3WL + 10SA
- Categorical (i.e. factorial) predictors are represented by binary-valued predictors: \(x_i = 0\) (reference level) or \(x_i = 1\) (the alternative level)
- Factor with \(n\) levels: \(n-1\) binary predictors
- Interpretation of \(\beta_i\) for categorical predictors: change from reference level to alternative level
- Additional information: http://www.let.rug.nl/~wieling/BCN-Stats/lecture3
Mixed-effects regression modeling: introduction
- Mixed-effects regression modeling distinguishes fixed-effect and random-effect factors
- Fixed-effect factors:
- Repeatable levels
- Small number of levels (e.g., Gender, Word Category)
- Same treatment as in multiple regression (treatment coding)
- Random-effect factors:
- Levels are a non-repeatable random sample from a larger population
- Often large number of levels (e.g., Subject, Item)
What are random-effects factors?
- Random-effect factors are factors which are likely to introduce systematic variation
- Some participants have a slow response (RT), while others are fast
= Random Intercept for Subject - Some words are easy to recognize, others hard
= Random Intercept for Item - The effect of word frequency on RT might be higher for one participant than another: e.g., non-native participants might benefit more from frequent words than native participants
= Random Slope for Item Frequency per Subject - The effect of subject age on RT might be different for one word than another: e.g., modern words might be recognized faster by younger participants
= Random Slope for Subject Age per Item
- Some participants have a slow response (RT), while others are fast
- Note that it is essential to test for random slopes!
Question 1
Random slopes are necessary!
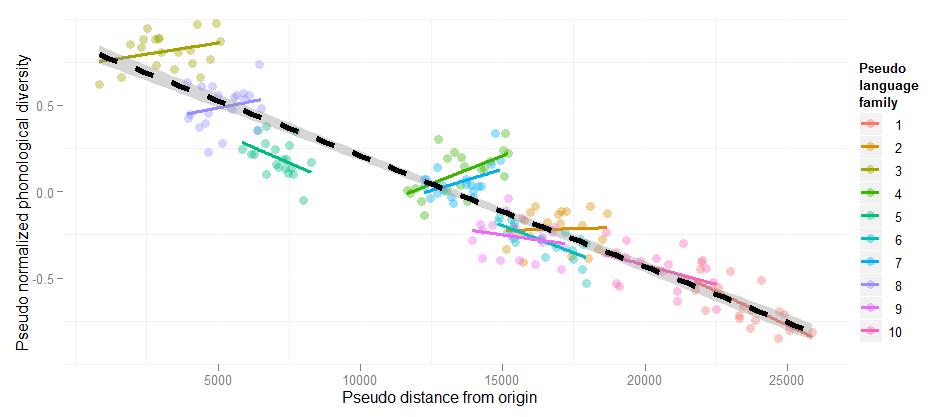
Estimate Std. Error t value Pr(>|t|)
Linear regression DistOrigin -6.418e-05 1.808e-06 -35.49 <2e-16
+ Random intercepts DistOrigin -2.224e-05 6.863e-06 -3.240 <0.001
+ Random slopes DistOrigin -1.478e-05 1.519e-05 -0.973 n.s.
This example is explained at the HLP/Jaeger lab blog
Specific models for every observation
- Mixed-effects regression allow us to use random intercepts and slopes (i.e. adjustments to the population intercept and slopes) to include the variance structure in our data
- Parsimony: a single parameter (standard deviation) models this variation for every random slope or intercept (a normal distribution with mean 0 is assumed)
- The adjustments to population slopes and intercepts are Best Linear Unbiased Predictors
- AIC comparisons assess whether the inclusion of random intercepts and slopes is warranted
- Note that multiple observations for each level of a random effect are necessary for mixed-effects analysis to be useful (e.g., participants respond to multiple items)
Specific models for every observation
- RT = 200 - 5WF + 3WL + 10SA (general model)
- The intercepts and slopes may vary (according to the estimated standard variation for each parameter) and this influences the word- and subject-specific values
- RT = 400 - 5WF + 3WL - 2SA (word: scythe)
- RT = 300 - 5WF + 3WL + 15SA (word: twitter)
- RT = 300 - 7WF + 3WL + 10SA (subject: non-native)
- RT = 150 - 5WF + 3WL + 10SA (subject: fast)
- And it is not hard to use!
lmer( RT ~ WF + WL + SA + (1+SA|Wrd) + (1+WF|Subj) )
lmerautomatically discovers random-effects structure (nested/crossed)
Specific models for every subject
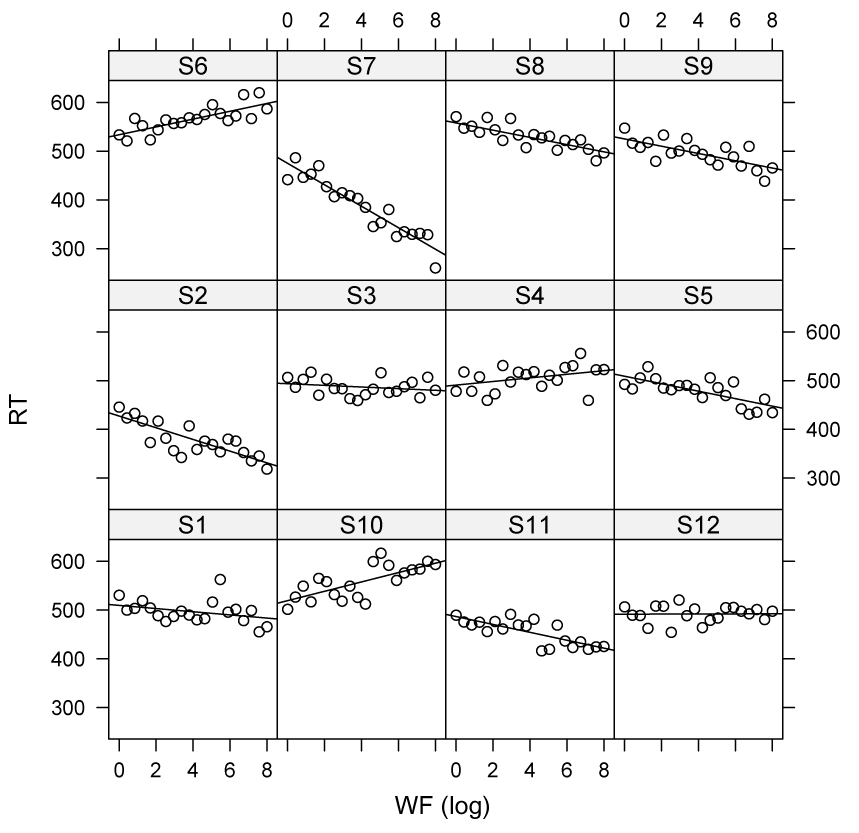
BLUPs of lmer do not suffer from shrinkage
- The BLUPS (i.e. adjustment to the model estimates per item/participant) are close to the real adjustments, as
lmertakes into account regression towards the mean (fast subjects will be slower next time, and slow subjects will be faster) thereby avoiding overfitting and improving prediction - see Efron & Morris (1977)
Question 2
Methodological issues
- Parsimony
- Centering
- Assumptions about the residuals
- Assumptions about the predictors
- We assume linearity, if this is not suitable you can use generalized additive modeling
- Model criticism
- How to select the "best" model?
Parsimony
- All models are wrong
- The correct model can never be known with certainty
- Some models are better than others
- Simpler models explaining the data are better than complex models
Center your variables (i.e. subtract the mean)
- Otherwise random slopes and intercepts may show a spurious correlation
- Also helps the interpretation of factorial predictors in model (marking differences at means of other variables, rather than at values equal to 0)
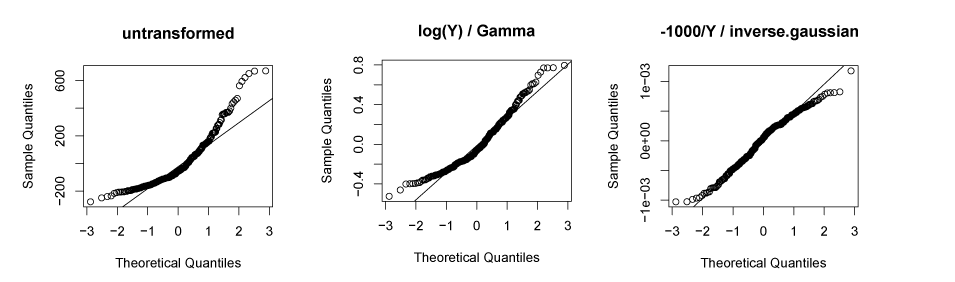
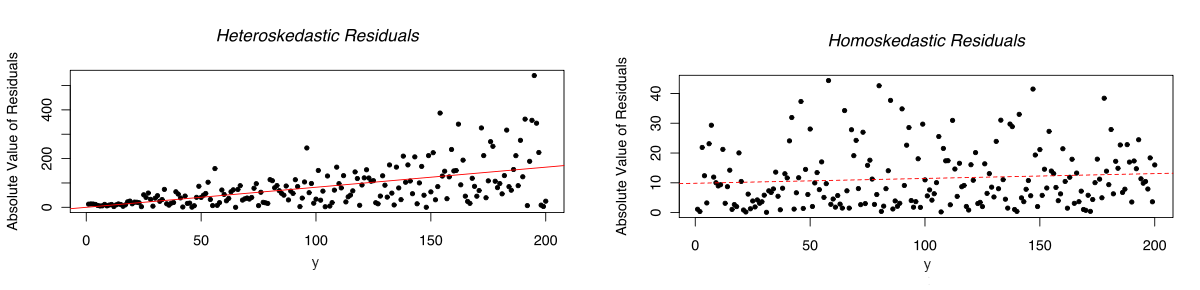
Residuals: normally distributed and homoskedastic
- In linear mixed-effects regression, the errors should follow a normal distribution with mean zero and the same standard deviation for any cell in your design, and for any covariate
- If not then transforming the dependent variable often helps: log(Y), or -1000/Y
- In some cases it is better to separate the distribution from the relationship between the dependent and independent variables by using generalized linear mixed-effects regression (e.g., Gamma distribution with identity link) as the distribution
Residuals: no trial-by-trial dependencies
- Residuals should be independent
- With trial-by-trial dependencies, this assumption is violated
- Possible remedies:
- Include trial as a predictor in your model
- Include the value of the dependent variable at the previous trial as a predictor
- (Note that GAMs have other facilities to correct for these dependencies)
Question 3
Trial-by-trial dependencies in a word naming task
- Word naming (reading aloud) of Dutch verbs
- Trial-by-trial dependencies in the residuals of the model
acf(resid(model), main=" ", ylab="autocorrelation function")
Taking into account trial-by-trial dependencies
Model criticism
- Check the distribution of residuals: if not normally distributed and/or hetereoscedastic residuals then use generalized linear mixed-effects regression modeling
- Check outlier characteristics and refit the model when large outliers are excluded to verify that your effects are not 'carried' by these outliers
- Important: no a priori exclusion of outliers without a clear reason
- A good reason is not that the value is over 2.5 SD above the mean
- A good reason (e.g.,) is that the response is faster than possible
- Important: no a priori exclusion of outliers without a clear reason
Model selection I
- "The data analyst knows more than the computer." (Henderson & Velleman, 1981)
- Get to know your data!
- There is no adequate automatic procedure to find the best model
- Fitting the most complex random effects structure (Barr et al., 2013) is mostly not a good idea
- The model may not converge, or is uninterpretable (see Baayen et al., forthcoming)
- The power of your method is reduced (Matuschek et al., forthcoming)
Model selection II
- My stepwise variable-selection procedure (for exploratory analysis):
- Include random intercepts
- Add other potential explanatory variables one-by-one
- Insignificant predictors are dropped
- Test predictors for inclusion which were excluded at an earlier stage
- Test possible interactions (don't make it too complex)
- Try to break the model by including significant predictors as random slopes
- Only choose a more complex model if it decreases AIC by at least 2
- Then the lowest AIC model is at least 2.7 (\(e^{\frac{\Delta\textrm{AIC}}{2}}\)) times more likely to represent the data
Model selection III
- For a hypothesis-driven analysis, stepwise selection is problematic
- Confidence intervals too narrow: \(p\)-values too low (multiple comparisons)
- See, e.g., Burnham & Anderson (2002)
- Solutions:
- Careful specification of potential a priori models lining up with the hypotheses (including random intercepts and slopes) and evaluating only these models (e.g., via AIC)
- This may be followed by an exploratory procedure
- Validating a stepwise procedure via cross validation (e.g., bootstrap analysis)
- Careful specification of potential a priori models lining up with the hypotheses (including random intercepts and slopes) and evaluating only these models (e.g., via AIC)
Case study: long-distance priming
- De Vaan, Schreuder & Baayen (The Mental Lexicon, 2007)
- Design
- long-distance priming (39 intervening items)
- base condition (
baseheid): base preceded neologism (fluffy - fluffiness) - derived condition (
heid): identity priming (fluffiness - fluffiness) - only items judged to be real words are included
- Prediction
- Subjects in derived condition (
heid) faster than those in base condition (baseheid)
- Subjects in derived condition (
- Dependent variable is log-transformed (but similar results using a GLMM)
A first model: counterintuitive results!
(note \(t > 2 \Rightarrow p < 0.05\), for \(N \gg 100\); R version 3.3.2 (2016-10-31), lme4 version 1.1.12)
library(lme4)
dat <- read.table("datprevrt.txt", header = T) # adapted primingHeid data set
dat.lmer1 <- lmer(RT.log ~ Condition + (1 | Word) + (1 | Subject), data = dat)
summary(dat.lmer1, cor = F)
# Linear mixed model fit by REML ['lmerMod']
# Formula: RT.log ~ Condition + (1 | Word) + (1 | Subject)
# Data: dat
#
# REML criterion at convergence: -102
#
# Scaled residuals:
# Min 1Q Median 3Q Max
# -2.359 -0.691 -0.134 0.590 4.261
#
# Random effects:
# Groups Name Variance Std.Dev.
# Word (Intercept) 0.00341 0.0584
# Subject (Intercept) 0.04084 0.2021
# Residual 0.04408 0.2100
# Number of obs: 832, groups: Word, 40; Subject, 26
#
# Fixed effects:
# Estimate Std. Error t value
# (Intercept) 6.6030 0.0421 156.7
# Conditionheid 0.0313 0.0147 2.1
Evaluation
- Counterintuitive inhibition
- But various potential factors are not accounted for in the model
- Longitudinal effects
- RT to prime as predictor
- Response to the prime (correct/incorrect): a yes response to a target associated with a previously rejected prime may take longer
- The presence of atypical outliers
An effect of trial?
dat.lmer2 <- lmer(RT.log ~ Trial + Condition + (1 | Subject) + (1 | Word), data = dat)
summary(dat.lmer2)$coef
# Estimate Std. Error t value
# (Intercept) 6.633384 4.67e-02 142.15
# Trial -0.000146 9.62e-05 -1.52
# Conditionheid 0.030977 1.47e-02 2.11
An effect of previous trial RT?
dat.lmer3 <- lmer(RT.log ~ PrevRT.log + Condition + (1 | Subject) + (1 | Word), data = dat)
summary(dat.lmer3)$coef
# Estimate Std. Error t value
# (Intercept) 5.8047 0.2230 26.03
# PrevRT.log 0.1212 0.0334 3.63
# Conditionheid 0.0279 0.0146 1.90
An effect of RT to prime?
dat.lmer4 <- lmer(RT.log ~ RTtoPrime.log + PrevRT.log + Condition + (1 | Subject) + (1 | Word), data = dat)
summary(dat.lmer4)$coef
# Estimate Std. Error t value
# (Intercept) 4.74877 0.2953 16.080
# RTtoPrime.log 0.16379 0.0319 5.141
# PrevRT.log 0.11901 0.0330 3.605
# Conditionheid -0.00612 0.0160 -0.383
An effect of the decision for the prime?
dat.lmer5 <- lmer(RT.log ~ RTtoPrime.log + ResponseToPrime + PrevRT.log + Condition + (1 | Subject) +
(1 | Word), data = dat)
summary(dat.lmer5)$coef
# Estimate Std. Error t value
# (Intercept) 4.7634 0.2923 16.30
# RTtoPrime.log 0.1650 0.0315 5.24
# ResponseToPrimeincorrect 0.1004 0.0226 4.45
# PrevRT.log 0.1142 0.0327 3.49
# Conditionheid -0.0178 0.0161 -1.11
An effect of the decision for the prime (in interaction)?
dat.lmer6 <- lmer(RT.log ~ RTtoPrime.log * ResponseToPrime + PrevRT.log + Condition + (1 | Subject) +
(1 | Word), data = dat)
summary(dat.lmer6)$coef
# Estimate Std. Error t value
# (Intercept) 4.3244 0.3152 13.72
# RTtoPrime.log 0.2276 0.0359 6.33
# ResponseToPrimeincorrect 1.4548 0.4052 3.59
# PrevRT.log 0.1183 0.0325 3.64
# Conditionheid -0.0266 0.0162 -1.64
# RTtoPrime.log:ResponseToPrimeincorrect -0.2025 0.0606 -3.34
- Interpretation: the RT to the prime is only predictive for the RT of the target word when the prime was judged to be a correct word
An effect of base frequency?
(Note the lower standard deviation of the random intercept for word: initial value was 0.058)
dat.lmer7 <- lmer(RT.log ~ RTtoPrime.log * ResponseToPrime + PrevRT.log + BaseFrequency + Condition +
(1 | Subject) + (1 | Word), data = dat)
summary(dat.lmer7)$varcor
# Groups Name Std.Dev.
# Word (Intercept) 0.0339
# Subject (Intercept) 0.1549
# Residual 0.2055
summary(dat.lmer7)$coef
# Estimate Std. Error t value
# (Intercept) 4.44098 0.31961 13.90
# RTtoPrime.log 0.21824 0.03615 6.04
# ResponseToPrimeincorrect 1.39705 0.40516 3.45
# PrevRT.log 0.11542 0.03246 3.56
# BaseFrequency -0.00924 0.00437 -2.11
# Conditionheid -0.02466 0.01618 -1.52
# RTtoPrime.log:ResponseToPrimeincorrect -0.19399 0.06055 -3.20
Testing random slopes: no main frequency effect!
dat.lmer7a <- lmer(RT.log ~ RTtoPrime.log * ResponseToPrime + PrevRT.log + BaseFrequency + Condition +
(1 | Subject) + (0 + BaseFrequency | Subject) + (1 | Word), data = dat)
summary(dat.lmer7a)$coef
# Estimate Std. Error t value
# (Intercept) 4.48231 0.31736 14.12
# RTtoPrime.log 0.21812 0.03595 6.07
# ResponseToPrimeincorrect 1.41675 0.40206 3.52
# PrevRT.log 0.10849 0.03235 3.35
# BaseFrequency -0.00795 0.00535 -1.48
# Conditionheid -0.02453 0.01603 -1.53
# RTtoPrime.log:ResponseToPrimeincorrect -0.19667 0.06008 -3.27
The model with random slope is better
AIC(dat.lmer7) - AIC(dat.lmer7a) # compare AIC
# [1] 3.65
# Alternative to AIC comparison: Likelihood Ratio Test
anova(dat.lmer7, dat.lmer7a, refit = F) # compares models
# Data: dat
# Models:
# dat.lmer7: RT.log ~ RTtoPrime.log * ResponseToPrime + PrevRT.log + BaseFrequency +
# dat.lmer7: Condition + (1 | Subject) + (1 | Word)
# dat.lmer7a: RT.log ~ RTtoPrime.log * ResponseToPrime + PrevRT.log + BaseFrequency +
# dat.lmer7a: Condition + (1 | Subject) + (0 + BaseFrequency | Subject) +
# dat.lmer7a: (1 | Word)
# Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
# dat.lmer7 10 -126 -78.3 72.8 -146
# dat.lmer7a 11 -129 -77.2 75.6 -151 5.65 1 0.017 *
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Testing for correlation parameters in random effects
dat.lmer7b <- lmer(RT.log ~ RTtoPrime.log * ResponseToPrime + PrevRT.log + BaseFrequency + Condition +
(1 + BaseFrequency | Subject) + (1 | Word), data = dat)
summary(dat.lmer7b)$varcor
# Groups Name Std.Dev. Corr
# Word (Intercept) 0.0344
# Subject (Intercept) 0.1291
# BaseFrequency 0.0136 0.41
# Residual 0.2035
AIC(dat.lmer7a) - AIC(dat.lmer7b) # correlation parameter not necessary
# [1] -1.14
anova(dat.lmer7a, dat.lmer7b, refit = F)$P[2] # p-value from anova
# [1] 0.353
Model criticism: normality
qqnorm(resid(dat.lmer7a))
qqline(resid(dat.lmer7a))
Model criticism: heteroscedasticity
plot(fitted(dat.lmer7a), resid(dat.lmer7a))
The trimmed model
dat2 <- dat[abs(scale(resid(dat.lmer7a))) < 2.5, ]
dat2.lmer7a <- lmer(RT.log ~ RTtoPrime.log * ResponseToPrime + PrevRT.log + BaseFrequency + Condition +
(1 | Subject) + (0 + BaseFrequency | Subject) + (1 | Word), data = dat2)
summary(dat2.lmer7a)$coef
# Estimate Std. Error t value
# (Intercept) 4.44735 0.28598 15.55
# RTtoPrime.log 0.23511 0.03200 7.35
# ResponseToPrimeincorrect 1.56001 0.35551 4.39
# PrevRT.log 0.09554 0.02926 3.27
# BaseFrequency -0.00815 0.00459 -1.78
# Conditionheid -0.03814 0.01435 -2.66
# RTtoPrime.log:ResponseToPrimeincorrect -0.21616 0.05316 -4.07
- items in the
heidcondition are responded faster to than those in thebaseheidcondition
The trimmed model
- Just 2% of the data removed and an improved fit (explained variance)
(noutliers <- sum(abs(scale(resid(dat.lmer7a))) >= 2.5))
# [1] 17
noutliers/nrow(dat)
# [1] 0.0204
cor(dat$RT, fitted(dat.lmer7a))^2
# [1] 0.521
cor(dat2$RT, fitted(dat2.lmer7a))^2
# [1] 0.572
Question 4
Checking the residuals of the trimmed model
library(car)
par(mfrow = c(1, 2))
qqp(resid(dat2.lmer7a))
plot(fitted(dat2.lmer7a), resid(dat2.lmer7a))
Bootstrap sampling to validate results
library(boot)
(bs.lmer7a <- confint(dat2.lmer7a, method = "boot", nsim = 1000, level = 0.95))
# 2.5 % 97.5 %
# .sig01 0.00e+00 0.040543
# .sig02 1.41e-05 0.021509
# .sig03 9.75e-02 0.190691
# .sigma 1.71e-01 0.189190
# (Intercept) 3.83e+00 4.994796
# RTtoPrime.log 1.74e-01 0.302521
# ResponseToPrimeincorrect 8.53e-01 2.255276
# PrevRT.log 3.66e-02 0.157534
# BaseFrequency -1.76e-02 0.000579
# Conditionheid -6.73e-02 -0.010342
# RTtoPrime.log:ResponseToPrimeincorrect -3.19e-01 -0.112836
Recap
- We have learned:
- how to interpret regression results
- how to use
lmerto conduct mixed-effects regression - how to include random intercepts and random slopes in
lmerand why these are essential when you have multiple responses per subject or item - how to conduct model criticism
- that ANOVA is less flexible than mixed-effecs regression
- After the break:
- http://www.let.rug.nl/wieling/statscourse/lecture1/lab
- Lab session contains additional information: how to do multiple comparisons, using other optimizers, and conducting logistic regression
- http://www.let.rug.nl/wieling/statscourse/lecture1/lab
- Next lecture: more about mixed-effects regression using eye-tracking data
Evaluation
Questions?
Thank you for your attention!