this text in English
Hoe breng je verschillen tussen geografische gebieden in kaart?
Stel, je hebt overal in het land mensen ondervraagd, en
hun uitspraak van een groot aantal woorden genoteerd.
Nu wil je weten in welke plaatsen
hetzelfde dialect gesproken wordt. Met andere woorden, je zou een overzicht
willen maken van de dialectgebieden in het land. Hoe doe je dat?
Of stel, je hebt over het hele continent exemplaren gevangen van een
zeldzaam kevertje, je hebt van al die exemplaren de specifieke
genetische kenmerken vastgesteld, en nu wil je de gebieden in kaart brengen
waarin de kevertjes leven met de grootste onderlinge verwantschap.
Laten we ons verder houden bij het voorbeeld van de dialecten.
Om te beginnen kun je voor elk woord kijken hoeveel de uitspraak verschilt tussen twee
plaatsen. Dat verschil kun je in een getal uitdrukken. (Een van de
technieken om dat verschil te bepalen is de Levenshteinmeting.
Hiervan vind je elders een demonstratie en
een korte uitleg.)
Als je het
gemiddelde berekent van de verschillen tussen alle woorden zoals die in
die twee plaatsen worden uitgesproken, dan heb je een getalsmaat voor
het verschil tussen die twee plaatsen. Herhaal je dit voor alle combinaties van
twee plaatsen, dan krijg je een tabel van verschillen. Je hebt dan een
afstandstabel voor heel het land, een tabel waar geen geografische afstanden
in staan, maar uitspraakverschillen.
Van afstanden naar onderlinge ligging: schalen in meerdere dimensies
Als je een tabel met verschillen tussen honderden plaatsen hebt, dan is daar
niet zomaar een globale indruk uit af te lezen. Hoe breng je die afstanden op
een overzichtelijke manier in beeld? We beginnen met als voorbeeld
slechts vier plaatsen, A tot en met D, waarvan de verschillen in
onderstaande tabel staan:
| A
| B
| C
| D
|
| A | 0,0
|
| B | 1,4 | 0,0
|
| C | 3,0 | 4,0 | 0,0
|
| D | 3,0 | 4,0 | 1,4 | 0,0
|
Laten we proberen deze verschillen grafisch weer te geven. We zetten de
plaatsen A en B naast elkaar, op een afstand van 1,4. Daarna voegen we plaats C
toe zodat de afstand tot plaats A 3,0 is en de afstand tot plaats B 4,0. Er vormt
zich een driehoek. Wanneer we nu plaats D proberen toe te voegen komen we
in de problemen. We kunnen D zo plaatsen dat de afstand met C 1,4 is en
met B 4,0, maar dan blijkt de afstand met A niet 3,0 te zijn, maar 3,5.
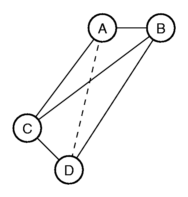
De enige mogelijkheid om de afstand precies goed te krijgen is door de vier
plaatsen in de driedimensionale ruimte te plaatsen.
Willen we deze vier plaatsen toch in het platte vlak afbeelden, dan moeten we
een beetje sjoemelen met de afstanden. We maken sommige afstanden wat
langer, andere wat korter, op zo'n manier dat het geheel zo min
mogelijk geweld wordt aangedaan. We krijgen dan een nieuwe afstandstabel:
| A
| B
| C
| D
|
| A | 0,00
|
| B | 1,10 | 0,00
|
| C | 3,03 | 4,10 | 0,00
|
| D | 3,03 | 4,10 | 1,44 | 0,00
|
Met deze verschillen zijn de plaatsen weer te geven:
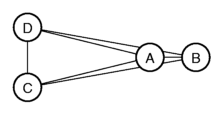
In de figuur kun je zien dat de plaatsen twee groepen vormen, een groep met
plaats A en B, en een groep met plaats C en D. De verschillen binnen de
groepen zijn klein in vergelijking met de verschillen tussen de twee groepen.
De techniek om elementen uit een tabel met verschillen af te beelden in een
ruimte met een beperkt aantal dimensies heet multi-dimensional
scaling, of "schalen in meerdere dimensies", kortweg MDS. Er
zijn verschillende algoritmes om MDS uit te voeren, en deze algoritmes
zijn vaak geïmplementeerd in programmatuur voor statistiek. De algoritmes
worden hier niet besproken.
Van schalen in meerdere dimensies naar een kleurenkaart
Het schalen in meerdere dimensies, MDS, werkt ook bij tabellen met verschillen
tussen honderden plaatsen, maar als we dat in het platte vlak willen
afbeelden, compleet met plaatsnamen, dan wordt het wel erg
onoverzichtelijk, met sommige plaatsen zo dicht op een kluitje dat de
plaatsnamen niet meer naast elkaar passen. Een ander probleem is dat MDS
in het platte vlak misschien te beperkt is om de variatie tussen de verschillende
gebieden goed weer te geven, omdat er geen rechtlijnig verband bestaat
tussen geografische afstanden en dialectverschillen.
Wat we eigenlijk willen is een landkaart waarop elk dialectgebied met een eigen
kleur is aangegeven. Hiervoor kunnen we MDS gebruiken op een vrij
simpele manier.
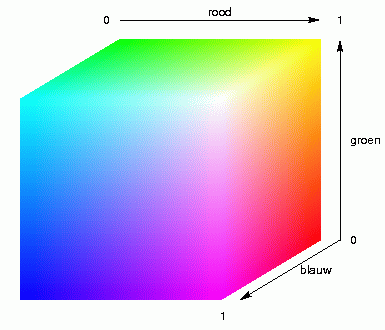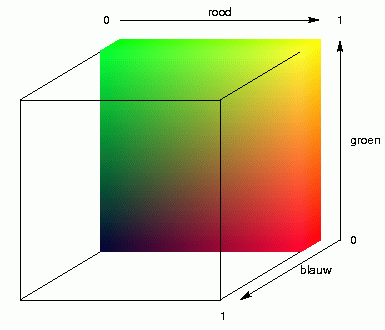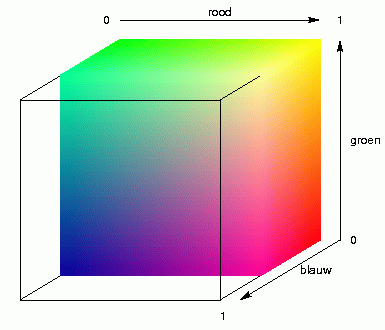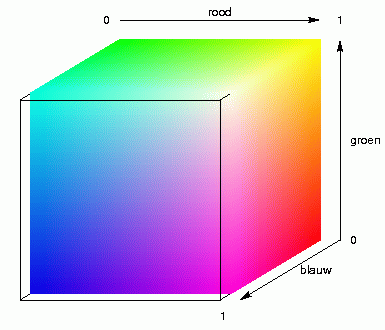

We beginnen met schalen, MDS, in drie dimensies. We zetten dus de plaatsen niet in
het platte vlak, ergens in een vierkant, maar in de ruimte, ergens in
een kubus. De afstanden tussen posities binnen de kubus geven aan
hoe groot het dialectverschil is tussen de plaatsen. Vervolgens vullen we
de kubus met kleur, zoals dat in de animatie hierboven links wordt gedemonstreerd.
Elke plaats krijgt nu de kleur toegewezen van de plek binnen de kubus waar
de plaats is neergezet, en met die kleur wordt de plaats op de landkaart
weergegeven. Het resultaat zie je in de kaart hieronder.
Nog eens met andere woorden.
Door MDS in drie dimensies uit te voeren geef je elke plaats drie coördinaten,
de x-, y- en z-coördinaat, een positie ergens in de breedte, de hoogte
en de diepte. Die drie coördinaten worden gebruikt als
waarden tussen licht en donker van drie kleurcomponenten: rood, groen en blauw.
Menging van deze primaire kleuren geeft de uiteindelijke kleur. De
animatie hierboven rechts laat dit zien voor lichte en donkere componenten
van rood, groen en blauw.
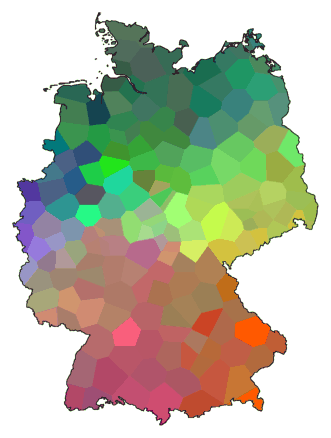
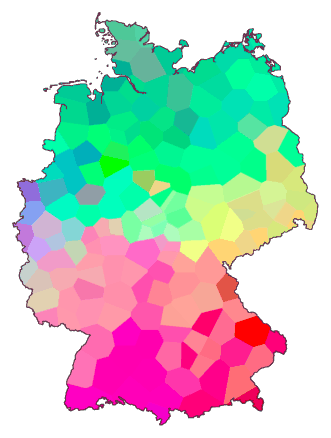
In deze kaart van Duitsland kun je een gebied in het noorden herkennen waar de
kleur groen overheerst, en een gebied in het zuiden waar roodtinten
overheersen. Hieraan is te zien dat er in het noorden een heel ander
dialect gesproken wordt dan in het zuiden. Je kunt ook zien dat langs
de kust, van de grens met Nederland tot aan de grens met Polen, ongeveer
hetzelfde dialect wordt gesproken.
Het samenvoegen van plaatsen in groepen: clustering
Nogmaals de tabel met afstanden tussen de plaatsen A, B, C en D:
| A
| B
| C
| D
|
| A | 0,0
|
| B | 1,4 | 0,0
|
| C | 3,0 | 4,0 | 0,0
|
| D | 3,0 | 4,0 | 1,4 | 0,0
|
Laten we nu eens de twee plaatsen met het kleinste onderlinge verschil
samenvoegen. Het kleinste verschil is 1,4. Deze waarde komt toevallig twee keer
voor, dus we kiezen gewoon een van de twee: A en B. Deze voegen we
samen, en we maken een nieuwe afstandstabel:
| A+B
| C
| D
|
| A+B | 0,0
|
| C | 3,5 | 0,0
|
| D | 3,5 | 1,4 | 0,0
|
De plaatsen A en B zijn nu vervangen door één element, genaamd A+B. Het verschil
tussen A+B en C stellen we gelijk aan het gemiddelde van het verschil
tussen A en C en het verschil tussen B en C. Hetzelfde doen we voor A+B
en D. (Het gebruik van het gemiddelde van de oude afstanden is slechts
een van verschillende methodes om de nieuwe
afstand te bepalen.)
Nu zoeken we weer naar de kleinste waarde in de (nieuwe) tabel, en dat is het verschil
tussen C en D. Deze voegen we samen, net als daarnet A en B:
Nu hebben we nog maar twee elementen over, een cluster van de plaatsen A en B,
en een cluster van de plaatsen C en D. Dit samenvoegen van plaatsen in
steeds grotere clusters, tot je nog maar enkele clusters over hebt,
wordt, hoe kan het ook anders, clustering genoemd. De stappen
van de clustering zoals hierboven gedaan kun je grafisch weergeven:
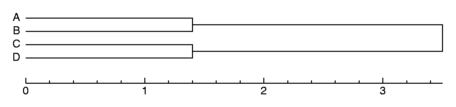
Zo'n afbeelding als hierboven wordt
dendrogram genoemd. De verticale
verbindingslijnen geven de afstand weer tussen de clusters toen ze werden
samengevoegd. In dit
dendrogram kun je weer zien dat A en B bij elkaar horen en C bij D.
Nu doen we hetzelfde met een tabel voor 186 plaatsen in Duitsland. Het
dendrogram wat je dan krijgt staat hieronder:

Met het dendrogram hebben we nog iets speciaals gedaan. We hebben een verticale
streep getrokken (de grijze lijn) en hebben elk cluster dat in z'n
geheel links van die lijn ligt een eigen kleur gegeven. Wat je krijgt
is een opdeling, een clustering, in acht groepen, en hoe die groepen dan
verder nog samen te voegen zijn tot grotere clusters wordt door de zwarte verbindingslijnen
aangegeven.
De plaatsnamen zijn in bovenstaand dendrogram weggelaten, waardoor de lijnen
wat dichter bij elkaar gezet konden worden. Die plaatsnamen hebben we
niet nodig, want het gaat nu even om de kleur die door de clustering
aan elke plaats wordt gegeven. Die kleuren kunnen we gebruiken om een
clusterkaart te tekenen:
Nog even ter vergelijking, de MDS-kleurenkaart en de clusterkaart naast elkaar:
Zie je hoe de kaarten in sommige opzichten elkaar tegen lijken te spreken?
Nadelen van de MDS-kleurenkaart
Een kleurenkaart heeft als meest voor-de-handliggend nadeel dat hij niet
gebruikt kan worden in een zwart-witpublicatie. En de meeste
wetenschappelijke publicaties op papier zijn nu eenmaal in zwart-wit, omdat
kleur te duur is.
Maar ook de kleurenkaart op zich heeft zo z'n tekortkomingen...

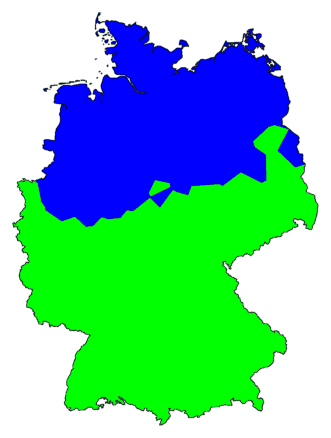
Hierboven links zie je nog eens de MDS-kleurenkaart. Daarnaast een clusterkaart
met slechts twee clusters, dat wil zeggen, een kaart die van alle grenzen
tussen clusters alleen de allerbelangrijkste laat zien. Zo'n clustering
krijg je door bij het clusteren net zo lang door te gaan met samenvoegen tot je nog maar
twee clusters overhebt.
Die grens tussen noord en zuid in de rechter kaart is dus, blijkbaar, de
belangrijkste dialectgrens in Duitsland. Is dat ook de opvallendste
grens in de MDS-kaart, links? Ik zelf zie in de linker kaart
verschillende begrenzingen, maar juist die zo belangrijke clustergrens,
die zie ik in het geheel niet. Ik ben dan ook kleurenblind.
Rood-groenkleurenblindheid is een erfelijke aandoening die bij mannen veel
voorkomt. Met deze kleurenblindheid zie ik wel het verschil tussen rood
en groen, maar als ik de drie kleuren rood, groen en blauw naast elkaar
zie, dan is het het blauw dat er heel opvallend uitspringt. Een zwak
contrast van blauwtinten valt bij mij veel meer in het oog, dan een
veel sterker rood-groencontrast. Kortom, ik zie in de MDS-kaart een
andere verdeling van dialecten dan iemand zonder kleurenblindheid.
Kijk nog eens naar de gekleurde kubus boven. Wat zou er gebeuren als je de
inhoud van die kubus zou draaien rond het middelpunt van de kubus? Alle
afstanden tussen de plaatsen in de kubus zouden gelijk blijven, maar de
plaatsen zouden in een andere kleur komen te liggen. Of kijk eens naar
onderstaande plaatjes:

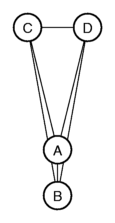
De figuur is geroteerd, de onderlinge afstanden zijn gelijk gebleven.
Met MDS worden alle punten zo gepositioneerd dat de onderlinge afstanden zo
goed mogelijk overeenkomen met de onderlinge verschillen, maar hoe het
geheel komt te liggen, dat is in wezen willekeurig gekozen. Evengoed
zouden de x-as en de y-as verwisseld kunnen zijn, of een as zou
gespiegeld kunnen zijn. De hele figuur zou zelfs over elke willekeurige
hoek gedraaid kunnen worden.
Dit alles houdt in dat je in een MDS-kleurenkaart willekeurig kleurcomponenten
kunt verwisselen of omdraaien. Formeel blijft de kaart hetzelfde, maar de
kaart komt er wel heel anders uit te zien:
Nu zetten we de nieuwe kleurenkaart naast de kaart met twee clusters:
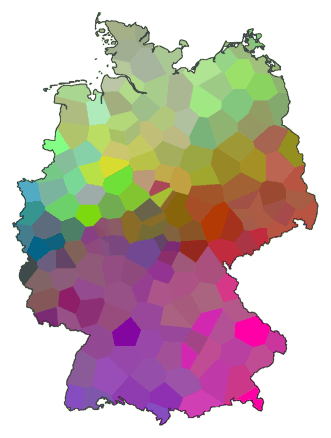

De clustergrens die eerst voor mij helemaal onzichtbaar was springt er nu voor mij als de
belangrijkste grens uit!
En dat is nog niet alles. De componenten rood, groen en blauw dragen op het
beeldscherm van een computer zeer verschillend bij aan het contrast
tussen licht en donker. Het verschil in licht en donker tussen blauw en
zwart is veel kleiner dan het verschil tussen groen en zwart.
Dus de toevallige ligging van de kleurcomponenten kan het beeld dat de
kaart te zien geeft sterk beïnvloeden.
Vraag: is dat ook zo voor mensen die niet kleurenblind zijn?
Wanneer je de kleurenkaart gaat afdrukken dan blijkt het contrast veranderd te
zijn. De groencomponent wordt op papier veel donkerder weergegeven
(in vergelijking met de andere kleurcomponenten) dan op het beeldscherm
van een computer.
Een aantal van deze problemen zouden verholpen kunnen
worden door gebruik te maken van iets wat een
CIE-standaard genoemd wordt, waarin
rekening gehouden wordt met perceptie van kleurcomponenten
door het menselijk oog. (Maar dit is ook geen oplossing voor kleurenblindheid.)
Hieronder zie je links de oorspronkelijke kleurenkaart, en rechts een kaart met
kleurcorrectie volgens CIE. (Het programma wat ik heb gebruikt om de
kaart te tekenen ondersteunt CIE niet volledig, en daarom durf ik niet
te zeggen of de kleuren in de rechter kaart correct zijn weergegeven.
TEKST AANPASSEN)

Tot slot: zoals je kunt zien heeft de kleurenkubus acht hoeken. Voor maximaal
contrast zijn slechts acht kleuren beschikbaar. Zijn er meer kleuren
nodig, dan moeten die daar tussengestopt worden. Waar het op neer komt
is dat als er dertig zeer uiteenlopende dialectgebieden zouden zijn
deze nooit allemaal in een MDS-kleurenkaart zichtbaar gemaakt kunnen worden.
Nadelen van de clusterkaart
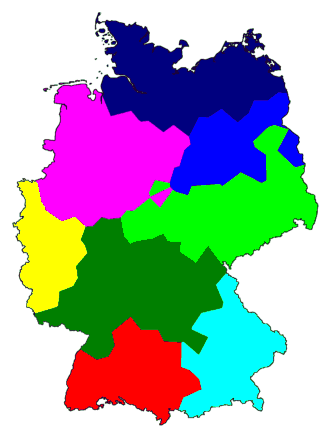
Bovenstaande kaart laat een aantal belangrijke vragen onbeantwoord:
- Wat is de belangrijkste clustergrens? Hoe is de grove opdeling in clusters
met grote verschillen, en de fijnere opdeling in clusters met
kleinere verschillen?
- Zouden er niet meer clusters zijn dan in deze kaart wordt weergegeven?
- Hoe scherp zijn de grenzen tussen de clusters werkelijk? Liggen ze precies
vast of zouden ze met kleine meetverschillen kunnen verschuiven? Met
andere woorden: wat zijn de harde grenzen, en wat zijn de zachtere
grenzen die vrij toevallig ergens in een gebied met geleidelijke
overgangen zijn getrokken?
In de kaart met acht clusters is niet te zien wat de belangrijkste clustergrens
is. Daarvoor moet je naar de kaart met maar twee clusters kijken. Als
je wilt zien hoe het gebied in stappen is op te delen, eerst de
splitsing van gebieden die sterk verschillen, daarna splitsing van
gebieden die minder van elkaar verschillen, dan heb je twee keuzes. Of
je zet een hele
reeks clusterkaarten op een rij, met in elke volgende kaart een cluster
meer dan in de kaart er voor. Of je zet een gekleurd dendrogram naast een
clusterkaart, zodat je uit het dendrogram kunt aflezen in welke volgorde
je gebieden moet samenvoegen om uit te komen bij de belangrijkere grenzen.
Hieronder nogmaals het dendrogram voor de dialecten in Duitsland:

Als de grijze verticale lijn een fractie naar links wordt verplaatst dan valt
het lichtgroene cluster uiteen in twee stukken, en zit je met negen clusters. Als je de lijn ietsje
naar rechts verplaatst, dan heb je nog maar zeven of zes clusters.
Hoeveel clusters zijn er werkelijk?
De acht clusters vormen op de kaart elk een mooi aaneengesloten gebied. Maar
houdt dat in dat de grenzen die je ziet in werkelijkheid ook
dialectgrenzen zijn? Niet per se.
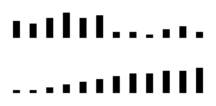
Hierboven zie je twee rijen van staafjes. De bovenste rij laat zich goed in
twee groepen delen. De linker helft bestaat uit lange staafjes, de
rechter helft uit korte staafjes. Een grenslijn precies middendoor
plaatst mooi de lange staafjes in een cluster links, en de korte staafjes
in een cluster rechts.
Nu de onderste rij staafjes. Ook deze rij kun je in twee groepen delen door een
grens in het midden te trekken, en inderdaad heb je dan links van de
grens een groep van staafjes die allemaal kleiner zijn dan de staafjes
in de groep rechts van de grens. Maar die grenslijn is heel
willekeurig. Evengoed kun je deze rij opdelen in drie groepen van gelijke
aantallen, en wat bij een indeling in twee groepen de grens was is dan
ineens het midden van een groep geworden.
Voor een clusterkaart geldt dat, ook al is een gebied nog zo mooi in twee
stukken verdeeld, je aan die kaart niet kunt zien of zich tussen die
twee gebieden daadwerkelijk een grens bevindt, of dat de lijn
vrij toevallig getrokken is door een groter gebied van gelijdelijke
veranderingen.
Een nieuw soort kaart: compositie van meerdere clusteringen
Ik stel een nieuw soort kaart voor: de
clustercompositiekaart. (Galgje!)
Kaarten van clustercomposities hebben geen van de beperkingen die besproken zijn
voor MDS-kleurenkaarten en gewone clusterkaarten. Daarnaast bieden
clustercomposities nog wat extra mogelijkheden. Met een kaart van een
clustercompositie kun je de verschillen tussen de gebieden beter in
beeld brengen dan met de andere kaarten.
Een kaart met een clustercompositie is een kaart waarop verschillende
clusteringen zijn samengevoegd. Dit doe je door niet elk cluster een
eigen kleur te geven, maar door de grenslijnen tussen de clusters te
tekenen. Je voert een aantal verschillende clusteringen uit, en
iedere keer wanneer een grenslijn op dezelfde plek getrokken wordt
kleur je dat lijnstukje ietsje donkerder. Je krijgt dan een kaart met
lichte en donkere lijnen.
Je kunt deze methode gebruiken om de stappen in een clustering te laten zien in
één kaart. Eerst verdeel je het gebied in twee clusters, en trek je de
grenslijn. Daarna verdeel je het gebied in drie clusters. Daarbij trek
je de eerste lijn nog een keer, en voeg je een nieuwe lijn toe. De
oude lijn is dan donkerder (twee keer getekend) dan de nieuwe lijn (nog
maar één keer getekend). De kaart hieronder laat dit zien voor een
opdeling van in totaal twaalf clusters.
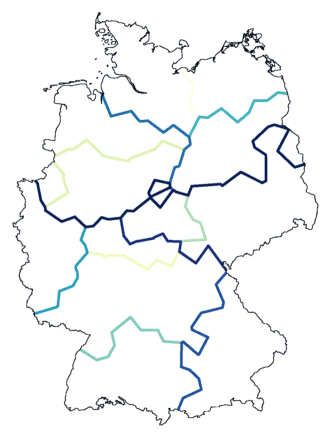
In de kaart hierboven is nog steeds niet te zien of een grens daadwerkelijk een
dialectgrens is. Dat kunnen we zichtbaar maken door gebruik te maken van
ruis.
De clustering is gebaseerd op een tabel van verschillen: meetgegevens. Hoe
betrouwbaar zijn die meetgegevens? En in het verlengde daarvan: hoe betrouwbaar is
de clustering gebaseerd op die meetgegevens? Je kunt dit toetsen door
de waarden in de tabel te variëren, en te kijken of dit effect heeft op
de clustering. Je voegt wat ruis toe, en is een grens tussen twee
gebieden heel scherp, dan zal die grens ook met wat ruis in de
meetgegevens er nog precies zo uitzien. Grenzen die niet zo scherp zijn
zullen misschien anders getrokken worden.
Onderstaande clustercompositie is gemaakt door de clustering vele malen te
herhalen, waarbij steeds ruis werd toegevoegd aan de meetgegevens.
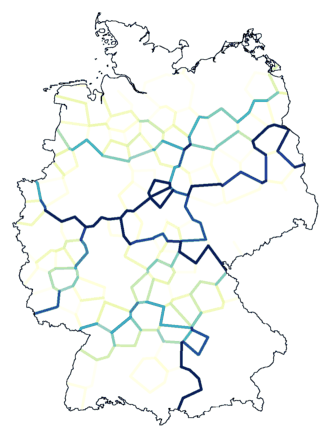
Sommige grenzen zijn heel duidelijk. De belangrijkste clustergrens, die tussen
noord en zuid, komt nog steeds als duidelijkste grens tevoorschijn, ook al
blijkt nu dat de precieze loop nabij Nederland niet helemaal vast ligt.
Helemaal in het zuiden is te zien dat er een duidelijk verschil is tussen oost
en west. Maar hoe de grenzen tussen deze gebieden en het gebied net ten noorden
daarvan lopen, dat blijft vaag.
Het dialect ten oosten van Overijssel en Gelderland verschilt van dat in de
buurt van Denemarken, maar de overgang is vrij geleidelijk, waardoor de
grens tussen beide dialecten niet precies valt te trekken.
Alle kaarten op deze pagina zijn gemaakt van dezelfde afstandmeting, en gebaseerd op dezelfde
clustermethode. Met clustercomposities is het ook mogelijk om de
resultaten van verschillende afstandmetingen en/of clustermethoden samen
te voegen.
En verder...
Voorbeelden
Hieronder worden nog een aantal kaarten herhaald. Een MDS-kaart of gewone
clusterkaart links, en een clustercompositie rechts. Ter vergelijking,
zonder verder commentaar.