Hoe bepaal je de juiste clustering van een gebied?

Voorkennis: clustering, schaling in meerdere dimensies (MDS), zie Hoe breng je verschillen tussen geografische gebieden in kaart?

Voor clustering bestaan er verschillende methodes, elk met zijn eigen specifieke kenmerken. Over de theorie achter de verschillende methodes gaat het hier niet. De aanpak hier is praktisch. We hebben een tabel met dialectverschillen tussen Duitse plaatsen, en willen kijken welke clustermethode we moeten gebruiken om de grenzen tussen dialecten te vinden.

We beginnen met de clustermethode die Ward's Method genoemd wordt, ook bekend onder de naam Minimum Variance. Alhoewel dit uiteindelijk niet de beste methode blijkt is het wel een bruikbare methode om mee te beginnen.

Ward's Method heeft een sterke neiging de data op te delen in groepen met ongeveer gelijke aantallen elementen. Dat houdt in dat als de "natuurlijke" clusters zeer verschillend zijn in omvang, dat dan de grotere clusters worden opgesplitst in stukken die ongeveer even groot zijn als de kleinere "natuurlijke" clusters.

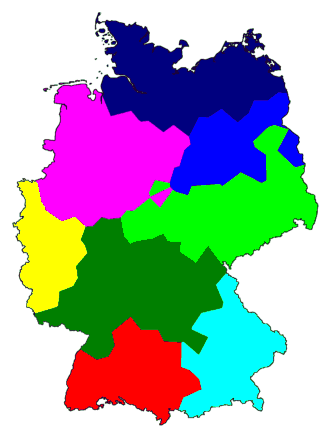
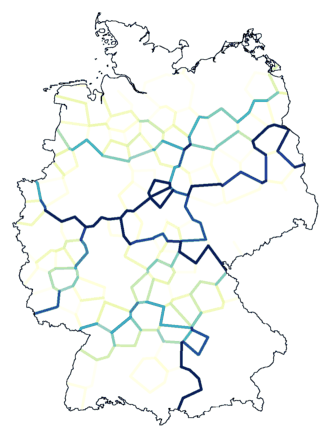
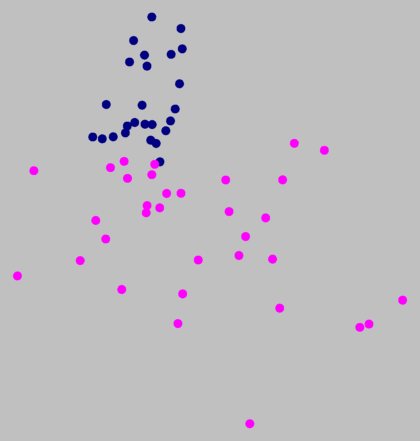
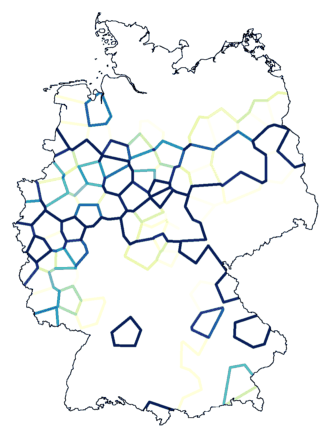
Clustering met ruis (hierboven, rechts, ruisniveau 1,5 op 8 clusters) suggereert dat de grens tussen magenta en donkerblauw (links) geen echte clustergrens is.

Het voordeel van Ward's Method is dat het geen "losse eindjes" laat hangen. Geen clusters met maar één, of enkele elementen. De gegevens worden allemaal samengevoegd in hanteerbare brokken die zich goed afzonderlijk nader laten bekijken. Daarvan gaan we nu gebruik maken. Hieronder zie je links steeds de clusterkaart, gemaakt met Ward's Method. De oorspronkelijke tabel met dialectverschillen schalen we in twee dimensies (multidimensional scaling, MDS). Het resultaat van die schaling zetten we in de grafiek naast de kaart, waarbij elke plaats de kleur van het bijbehorende cluster krijgt.

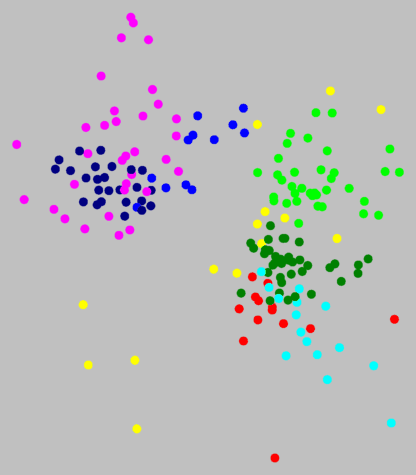
Hierboven rechts is te zien dat de clusters van magenta, donkerblauw en middelblauw samen een aparte groep vormen die duidelijke afstaat van de andere groep die gevormd wordt door de andere clusters. Hieraan kun je zien dat de grens tussen deze twee hoofdgroepen de voornaamste dialectgrens is. Dit is de grens tussen Laag-Duits in het noorden, en Hoog-Duits in het zuiden.

Nu gaan we naar delen van Duitsland kijken. Aan de hand van de clusterkaart selecteren we een aantal groepen die we nader willen onderzoeken. We maken een kleinere afstandstabel, met alleen die afstanden tussen de plaatsen uit de groepen die ons interesseren. Die kleinere afstandstabel gaan we opnieuw schalen in twee dimensies. Doordat een groot deel van de punten is verwijderd is er meer ruimte om de clusters in de overgebleven gebieden "uit elkaar te trekken".

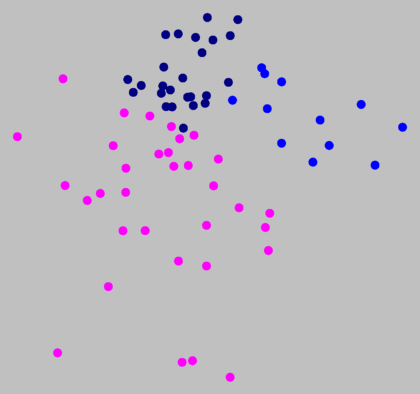
Als je in de grafiek hier rechtsboven kijkt zie je dat de punten van één kleur netjes bij elkaar liggen. Er liggen geen punten van verschillende kleuren door elkaar. Maar er is ook geen duidelijke afstand tussen de verschillende kleurgroepen. De grens is geen natuurlijke grens, maar een kunstmatige opdeling door de clustermethode.

Hierboven is het lichtere blauw verwijderd, en zijn de twee overgebleven groepen opnieuw geschaald in twee dimensies. Weer is te zien dat er geen duidelijke grens is tussen de twee clusters. Als je de kleur zou weglaten, zoals hieronder links is gedaan, zou je dan uit de grafiek zelf een tweedeling kiezen die overeen kwam met de deling zoals die door Ward's Method is gemaakt?

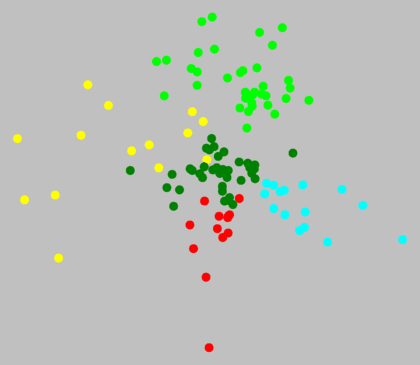
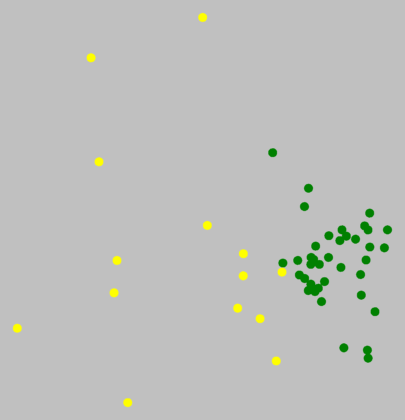
In het zuiden zijn lichtgroen en cyaan duidelijk aparte clusters. Maar hoe zit het met rood en donkergroen? Hieronder is tussen rood en donkergroen geen duidelijke grens te zien.

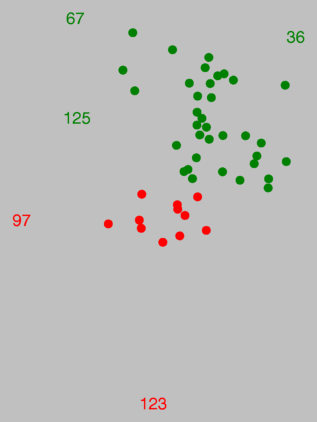
In de grafiek rechts hierboven zijn een aantal stippen vervangen door nummers. Deze nummers zijn ook in de kaart links weergegeven. Op deze manier kun je niet alleen naar groepen van plaatsen kijken, maar ook naar plaatsen afzonderlijk. Je kunt bijvoorbeeld, zoals hierboven, aangeven waar de meest "uitzonderlijke" plaatsen zijn. Of het dan in werkelijkheid gaat om plaatsen waar het dialect relatief sterk afwijkt van het dialect in de omgeving, of dat je in dit geval hebt te maken met minder betrouwbare gegevens, dat is iets wat je verder zou kunnen onderzoeken.

In het noorden waren geen clustergrenzen aan te wijzen, dus geen dialectgrenzen. Dat wil niet zeggen dat in heel het gebied hetzelfde dialect gesproken wordt. De uitspraak in het noord-oosten kan sterk verschillen van dat in het noord-westen, maar de verandering van dialect van noord-oost naar noord-west verloopt zo geleidelijk dat er met onze meetgegevens geen aparte gebieden zijn aan te wijzen. Wat wel is te zien is dat het geografisch verloop niet overal even snel gaat. In het magenta gebied zijn de onderlinge verschillen veel groter dan in het donkerblauwe gebied.

Dit verschil is er ook in het zuiden. De verschillen in het gele gebied zijn veel groter dan de verschillen in het donkergroene gebied. De gele stippen nemen het overgrote deel van de MDS-grafiek in (rechtboven), terwijl het donkergroene gebied in werkelijkheid een veel groter gebied is (linksboven).

Nu komen we bij de vraag: wat is in dit geval de juiste clustermethode? Ward's Method was bruikbaar om de zaak nader te bestuderen, maar het totaalbeeld dat deze clustering geeft klopt niet.

Het blijkt dat, in dit geval, een methode die Weighted Average wordt genoemd (ook bekend als McQuitty) een realistische weergave geeft.

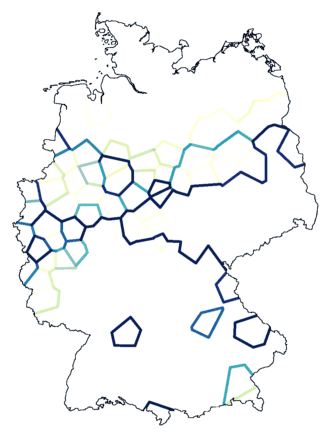
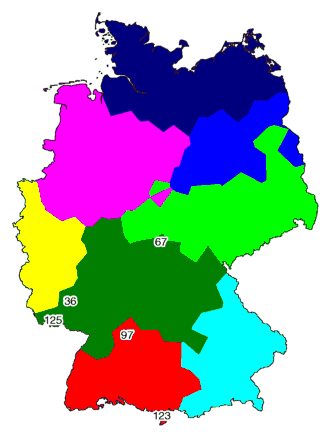
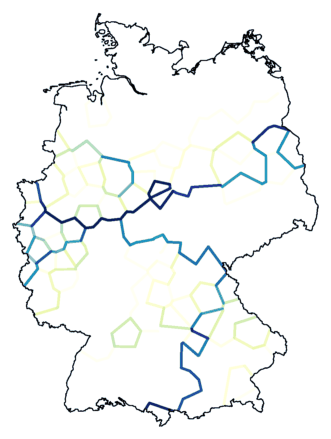
Hieronder is in de rechter kaart het resultaat te zien van clustering met ruis (combinatie van niveaus 1,0 en 1,5) over acht groepen. Het noordelijk gebied is niet opgedeeld in clusters, en ook tussen het rode en donkergroene gebied is geen grens te zien.

De plaatsen met de nummers 97 en 123 in het rode gebied zijn de plaatsen die, zo bleek met schaling in twee dimensies, nogal uitzonderlijk zijn. Zie hoe deze twee plaatsen hieronder in de rechter kaart zijn afgegrensd.

Een clustermethode die verwant is aan Weighted Average is Group Average. Deze methode blijkt in dit geval niet zo goed te werken. Dat wil niet zeggen dat Weighted Average altijd beter is dan Group Average!

Hieronder zie je twee kaarten gemaakt door clustering met ruis (zelfde ruisniveaus als bij Weighted Average), links in 16 clusters, rechts in 26 clusters. De grens tussen cyaan en rood, wat toch een belangrijke grens bleek te zijn, is met deze clustering niet of nauwelijks zichtbaar. (Rood: Swabisch, verwant aan het Zwitsers. Cyaan: Beiers, sterk verwant aan het Oostenrijks.)

Hieronder nog eens twee clustermethodes naast elkaar. Met ruis. Links staat de kaart gemaakt met Ward's Method, waar we mee zijn begonnen. Rechts Weighted Average, wat bleek het beste te zijn.