How to determine the best clustering of an area

Required knowledge: clustering, multi-dimensional scaling (MDS), see How to map difference between geographic areas

There exist several methods to do clustering, each with its own characteristics. The theory behind these methods will not be discussed here. Our approach is practical. We have a table with dialect differences between places in Germany, and want to know which clustering methods to use to find the borders between the different German dialects.

We start with a clustering method that goes by the name of Ward's Method. It is also known as Minimum Variance. Though in the end, this method does not turn out to be the best one, it is very useful as a method to start with.

Ward's Method has a strong tendency to split data in groups of roughly equal size. This means that when the "natural" clusters differ much in size, then the big ones will be split in smaller parts roughly equal in size to the smaller "natural" clusters.

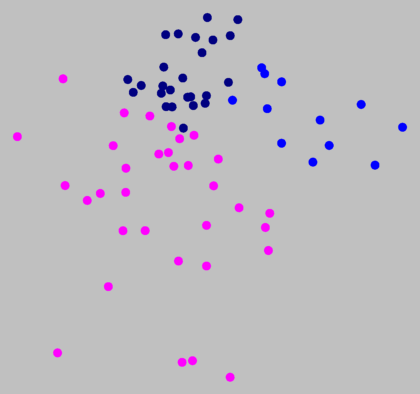
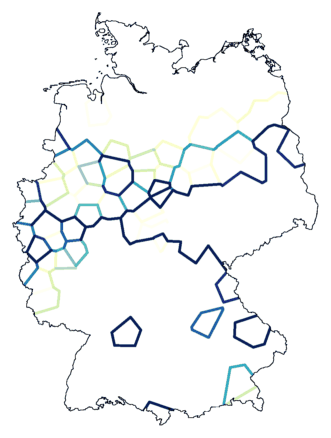
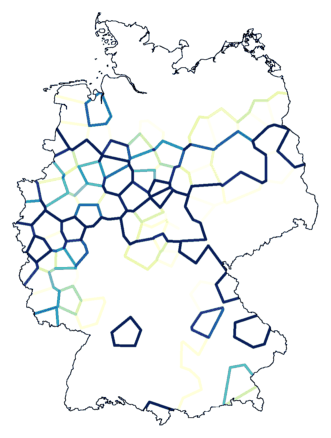
Clustering with noise (above, right, noise level 1.5 on 8 clusters) suggests that the border between magenta and dark blue (above, left) is not a true cluster border.

The advantage of Ward's Method is that it doesn't leave any "loose ends". No clusters with only one or a few elements. All data is grouped in bite size chunks, which can be studied further quite easily. Now we will make use of this property. Below, on the left side, you will see cluster maps made with Ward's Method. We use multi-dimensional scaling (MDS) on the table of differences to map the places into two dimensions, and the results is shown in the graph to the right of each map. Each place in the MDS graph to the right will have the same colour as it has in the map on the left.

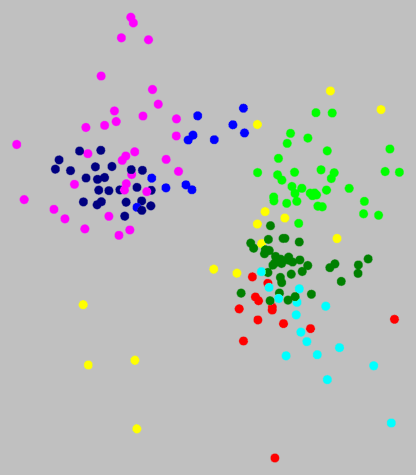
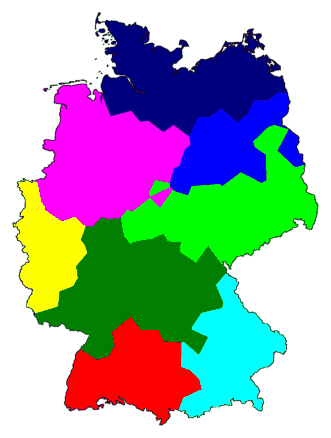
Above, right, you can see that the magenta, dark blue, and medium blue clusters are part of one big group that stands apart from the other group. This shows the primary dialect border of Germany. The north is the area of Low German, the south that of High German.

Now we focus on parts of Germany. From the map on the left, we selects a number of clusters we want to examine more closely. We make a smaller table of differences, a table that has only the differences between the places of the areas we are interested in. Then we apply MDS to that smaller table. Because a large part of the original places are removed, there is more room available to "pull apart" the remaining clusters.

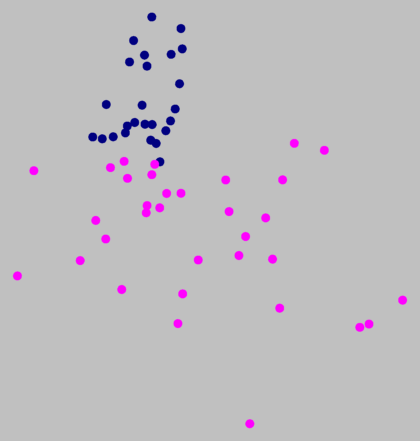
If you look at the graph above right, you see all the places nicely grouped by colour. There are no points with different colours mixed in one region. However, there is no clear distance between the tree colour groups. The borders are not natural, but an artifact of the clustering method.

Above, the places from the medium blue group are removed. MDS is applied to the two remaining groups. Again, no visually clear border between the clusters. If we didn't use colour (below, left), would you split the dots over the same two groups as was done by clustering with Ward's Method?

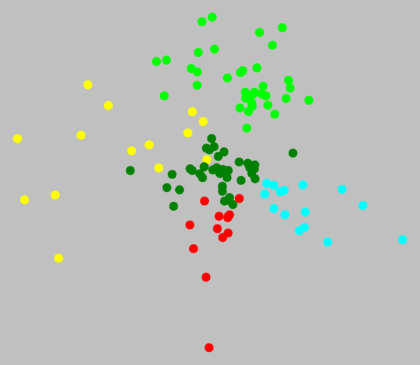
In the south, bright green and cyan are distinct clusters. But what about red and dark green? Below, there is no visual border.

In the graph above right, some dots are replaced with numbers. These numbers correspond to those in the map on the left. This allows you not only to look at groups, but also at individual places within each group. As is done above, you can mark the most exceptional places. Whether the dialect of these places really is markedly distinct from that in the surrounding area, or whether your data from these places may be less reliable, that is something you might choose to investigate.

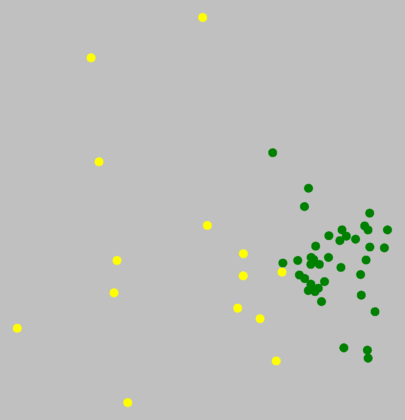
Within the north, there were no true cluster borders, which means, no dialect borders. That does not mean that the dialect is the same everywhere in the north. The pronunciation in the north-east can be very different from that in the north-west, but the transition from one end of the area to the other is gradual, and with our data, we cannot identify any distinct sub-areas. On the other hand, what is visible is that the amount of transition across the north differs. In the magenta area, the mutual differences are relatively large compared to the mutual differences in the dark blue area.

Such a difference also exists in the south. The mutual differences in the yellow area are much larger than those in the dark green area. The yellow dots use up most of the space in the MDS plot (above, right), even though in reality, the dark green area is much larger (above, left).

Now we get to the question: which clustering method should we use in our case? Ward's Method was useful as a tool for exploration, but the overall picture emerging from the clustering is not correct.

It turns out that, in this case, a method known as Weighted Average (also known as McQuitty) results in the best representation.

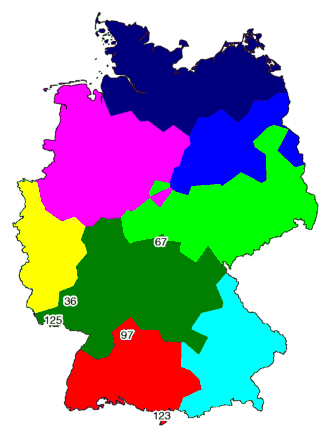
The map below right shows the result of clustering with noise (combined noise levels of 1.0 and 1.5 ) into eight groups. The north is not divided into clusters, and the former red and dark green area is not separated by a cluster border.

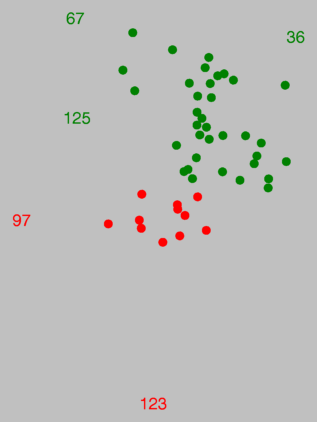
The places with numbers 97 and 123 in the red area are rather exceptional, as was shown by MDS. Note how these places are marked in the map on the right.

A clustering method related to Weighted Average is Group Average. This method does not work well in this case. That does not mean that Weighted Average is always better than Group Average!

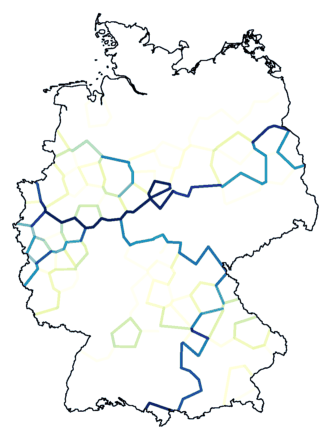
Below are two maps resulting from clustering with noise (same levels as used with Weighted Average), on the left with 16 clusters, on the right with 26 clusters. De border between cyan and red, which was shown to be an important dialect border, is invisible or nearly invisible. (Red: Schwabian, related to Swiss. Cyan: Bavarian, strongly related to Austrian.)

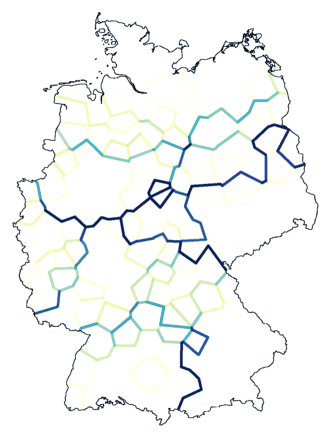
Below, again the results of two clusterings. Using noise. On the left the map made with Ward's Method, the method we started with. On the right the map with Weighted Average, which turned out to be the best method.