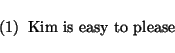
may be analyzed in some PATR grammar in a way that gives rise to the derivation tree in figure 1.
In formalisms such as PATR II the string associated with a derivation is the sequence of terminal nodes of the corresponding derivation tree in left-to-right order. For example, the sentence
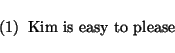
may be analyzed in some PATR grammar in a way that gives rise to the derivation tree in
figure 1.
In sign-based approaches such as in UCG and HPSG the string does not have any special status but is part of an attribute of each feature structure (sign). The attribute is usually called `phon', `string', `graph' or `orth' (I will use `string' in the following). Hence, the string associated with a construction is simply the value of the `string' feature of the sign that is assigned to the construction. In UCG there is a condition called `adjacency' condition, which says that signs can combine only if they are adjacent. In other words, the value of the `string' feature of a mother node in a parse tree is always the concatenation of the `string' features of the daughter nodes. Hence, the UCG parse tree for the foregoing example presumably would be someting like figure 2.
The two approaches are formally equivalent, but the second approach has the advantage that it at least becomes easier to think of other `modes' of combination of the value of the `string' attribute. As an example consider
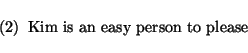
Suppose that there is linguistic motivation that in this sentence, as
in sentence 1, the sequence `easy to please' should be
regarded as a (discontinuous) constituent. Such an analysis can not be
defined directly in PATR or UCG. If no adjancency condition applied we
could have a parse tree of `easy person to please' as in
figure 3.
Clearly it is possible to define such an analysis in PATR or UCG in an indirect way by the usuqal threading of information through intermediate nodes (remember that both systems are Turing equivalent). However, these threading techniques usually become rather complex and make it difficult to define a semantics which is compositional. Furthermore, it is easier to define generation algorithms if the semantics is built in a systematically constrained way. The semantic-head-driven generation strategy discussed in the previous chapter faces problems in case semantic heads are `displaced', and this displacement is analyzed using threading. However, in this chapter I sketch a simple analysis of verb-second (an example of a displacement of semantic heads) by an operation similar to head wrapping which a head-driven generator processes without any problems (or extensions) at all.