More powerful string operations

Next: F-LCFRS Up: Beyond concatenation Previous: Concatenative systems

More powerful string operations

Head wrapping

[19] proposes a grammatical formalism called Head Grammar (HG). HG is a slightly more powerful formalism than context-free grammar. The extra power is available through head wrapping operations. A head wrapping operation manipulates strings which contain a distinguished element (its head). Such headed strings are a pair of an ordinary string, and an index (the pointer to the head), for example $\langle$ w₁w₂w₃w₄, 3 $\rangle$ is the string w₁w₂w₃w₄ whose head is w₃. Ordinary grammar rules define operations on such strings. Such an operation takes n headed strings as its arguments and returns a headed string. A simple example is the operation which takes two headed strings and concatenates the first one to the left of the second one, and where the head of the second one is the head of the result (this shows that the operations subsume ordinary concatenation). The rule is labelled LC2 by Pollard:

LC2( $\displaystyle \langle$ $\displaystyle \sigma$ , j $\displaystyle \rangle$ , $\displaystyle \langle$ $\displaystyle \tau$ , i $\displaystyle \rangle$ ) : = $\displaystyle \langle$ $\displaystyle \sigma$ $\displaystyle \tau$ , i $\displaystyle \rangle$

The following example shows that head-wrapping operations are in general more powerful than concatenation. In this example the second argument is `wrapped' around the first argument:

RL2( $\displaystyle \langle$ $\displaystyle \sigma$ , j $\displaystyle \rangle$ , $\displaystyle \langle$ t₁...t_n, i $\displaystyle \rangle$ ) : = $\displaystyle \langle$ t₁...t_i $\displaystyle \sigma$ t_{i + 1}...t_n, i $\displaystyle \rangle$

As an example, Pollard presents a rule for English auxiliary inversion:

S[+ INV] $\displaystyle \rightarrow$ RL2(NP, VP[+ AUX])

which may combine the noun phrase `Kim' and the verb phrase `must go' to yield `Must Kim go', with head `must'.

The motivation Pollard presents for extending context-free grammars (in fact, GPSG), is of a linguistic nature. Especially so-called discontinuous constituencies can be handled by HG whereas they constitute typical puzzles for GPSG. Apart from the above mentioned subject-auxiliary inversion he discusses the analysis of `transitive verb phrases' based on [1]. The idea is that in sentences such as

$\begin{exam} Sandy persuaded Kim to leave \end{exam}$
`persuaded' + `to leave' form a (VP) constituent, which then combines with the NP object ('Kim') by a wrapping operation.

Yet another example of the use of head-wrapping in English are the analyses of the following sentences.

$\begin{exams} \item Kim is much taller than Sandy \item Kim is a much taller person than Sandy \end{exams}$
$\begin{exams} \item Kim is very easy to please \item Kim is a very easy person to please \end{exams}$
where in the first two cases `taller than Sandy' is a constituent, and in the latter examples `easy to please' is a constituent.

Breton and Irish are VSO languages, for which it has been claimed that the V and the O form a constituent. Such an analysis is readily available using head wrapping, thus providing a non-transformational account of [16].

Finally, Pollard also provides a wrapping analysis of Dutch cross-serial dependencies.

Johnson's `combines'

[11] discusses an extenstion of DCG in order to analyse the Australian free word-order language `Guugu Yimidhirr'. In ordinary DCG a category is associated with a pair indicating which location the constituent occupies. Johnson proposes that constituents in the extended version of DCG be associated with a set of such pairs. A constituent thus `occupies' a set of continuous locations. The following is a sentence of Guugu Yimidhirr:

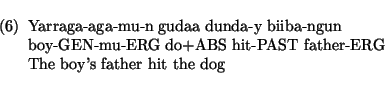
$\begin{exam} \begin{flushleft} Yarraga-aga-mu-n gudaa dunda-y biiba-ngun\\ boy-... ...BS hit-PAST father-ERG\\ The boy's father hit the dog \end{flushleft}\end{exam}$
In this sentence, the discontinuous constituent `Yarraga-aga-mu-n ...biiba-ngun' (boy's father) is associated with the set of locations:

{[0, 1],[3, 4]}

Johnson notices that such expressions can be represented with bit vectors. In a grammar rule the sets of locations of the daughters of the rule are `combined' to construct the set of locations associated with the daughters. The predicate combines(s₁, s₂, s) is true iff s is equal to the (bit-wise) union of s₁ and s₂, and the (bit-wise) intersection of s₁ and s₂ is null (ie. s₁ and s₂ must be non-overlapping locations). Grammars which exclusively use this predicate, are permutation-closed. For Guugu Yimidhirr Johnson also proposes a concatenative rule for possesive noun constructions in which the possesive is identified by position rather than by inflectional markings. Apart from these constructions Guugu Yimidhirr is said to be permutation-closed (Johnson, quoting [9]). Earley deduction [18] is used as a general proof procedure for such extended DCG grammars.

Sequence union

[21], and [22] discuss an operation called sequence union to analyze discontinuous constituents. The sequence union of two sequences s₁ and s₂ is the sequence s₃ iff each of the elements in s₁ and s₂ occur in s₃, and moreover, the originial order of the elements in s₁ and s₂ is preserved. For example, the sequence union of the sequences $\langle$ a, b $\rangle$ and $\langle$ c, d $\rangle$ is any of the sequences:

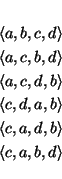
$\eq \lefteqn{\langle a,b,c,d\rangle}~~~~\\ \lefteqn{\langle a,c,b,d\rangle}~~~~... ...efteqn{\langle c,a,d,b\rangle}~~~~\\ \lefteqn{\langle c,a,b,d\rangle}~~~~ \eeq$

Reape presents an HPSG-style grammar [20] for German and Dutch which uses the sequence union relation on word-order domains. The grammar handles several word-order phenomena in German and Dutch. Word-order domains are sequences of signs. The phonology of a sign is the concatenation of the phonology of the elements of its word-order domain. In `rules', the word-order domain of the mother sign is defined in terms of the word-order domains of its daughter signs. For example, in the ordinary case the word-order domain of the mother simply consists of its daughter signs. However, in specific cases it is also possible that the word-order domain of the mother is the sequence union of the word-order domains of its daughters.

The following German example by Reape clarifies the approach, where I use indices to indicate to which verb an object belongs.

$\begin{exam} \begin{flushleft} \dots es$_i$\ ihm$_j$\ jemand$_k$\ zu lesen$_i$\ ... ...ised had\\ (i.e. someome had promised him to read it) \end{flushleft}\end{exam}$
Figure 4 shows a parse tree of this sentences where the nodes of the derivation tree are labelled by the string associated with that node. Note that strings are defined with respect to word-order domains. Sequence union is defined on such domains. The strings of the derivation tree are thus only indirectly related through the corresponding word-order domains.

**Figure 4:** Parse tree of sequence union example
$\begin{figure} \setlength{\unitlength}{1pt}% \begin{picture} (400,200)(-20,-20) ... ...60,55){\line(-1,-1){45}} \put(260,55){\line(1,-1){45}} \end{picture}\end{figure}$

Linear precedence statements are defined with respect to word-order domains. These statements can be thought of either as well-formedness conditions on totally ordered sequences, or alternatively as constraints further limiting possible orders of a word-order domain. Note that order information is monotonic; the sequence union relation can not `change' the order of two ordered items.

Next: F-LCFRS Up: Beyond concatenation Previous: Concatenative systems

Noord G.J.M. van
1998-09-30