The head corner parser

This section describes the head-driven parsing algorithm for the type of grammars described above. The parser is a generalization of Kay's head-driven parser, which in turn is a modification of a left-corner parser. The parser, which may be called a `head-corner' parser,¹ proceeds in a bottom-up way. Because the parser proceeds from head to head it is easy to use powerful top-down predictions based on the usual head feature percolations, and subcategorization requirements that heads require from their arguments.
In fact, the motivation for this approach to parsing discontinuous constituency is already hinted at by Mark Johnson [11]:

In left-corner parsers [15] the first step of the algorithm is to select the left-most word of a phrase. The parser then proceeds by proving that this word indeed can be the left-corner of the phrase. It does so by selecting a rule whose leftmost daughter unifies with the category of the word. It then parses other daughters of the rule recursively and then continues by connecting the mother category of that rule upwards, recursively. The left-corner algorithm can be generalized to the class of grammars under consideration if we start with the lexical head of a phrase, instead of its leftmost word. Furthermore the head_corner predicate then connects smaller categories upwards by unifying them with the head of a rule. The first step of the algorithm consists of the prediction step: which lexical entry is the lexical head of the phrase? The first thing to note is that the words introduced by this lexical entry should be part of the input string, because of the nonerasure requirement. Therefore we use the bag of words as a `guide' [5] as in a left-corner parser, but we change the way in which lexical entries `consume the guide'. For the moment I assume that the bag of words is simply represented with the string, but I introduce a better datastructure for bags in the next section. Hence to get things going I define the predicate start_parse/1 as follows:

$\pr\pred \head{start\_parse(Sign) {\mbox{\tt :-}}} \body{string(Sign,String),} \body{parse(Sign,String,\langle\rangle).} \epred\epr$

Furthermore in most linguistic theories it is assumed that certain features are shared between the mother and the head. I assume that the predicate head/2 defines these feature percolations; for the grammar of the foregoing section this predicate was defined as:

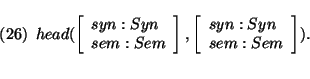
$\pr\pred \head{head(\avm{ syn: Syn\\ sem: Sem},\avm{ syn: Syn\\ sem: Sem}).} \epred\epr$

As we will proceed from head to head these features will also be shared between the lexical head and the top-goal; hence we can use this definition to restrict lexical lookup by top-down prediction. ² The first step in the algorithm is defined as:

$\pr\pred \head{parse(Goal,P_0,P) {\mbox{\tt :-}}} \body{predict\_head(Goal,Lex,P... ...ody{lex(Lex),} \body{string(Lex,Words),} \body{subset(Words,P_0,P).} \epred\epr$
Instead of taking the first word from the current input string, the parser may select a lexical entry dominating a subset of the words occuring in the input string, provided this lexical entry can be the lexical head of the current goal. The predicate subset(L₁, L₂, L₃) is true in case L₁ is a subset of L₂ with complement L₃. Later we will improve on the indexing of lexical entries.

The second step of the algorithm, the head_corner part, is identical to the left_corner part of the left-corner parser, but instead of selecting the leftmost daughter of a rule the head-corner parser selects the head of a rule. Remember that nonunit rules are represented as:

$\pr\pred \head{head\_corner(X,X,P,P).} \head{head\_corner(Small,Big,P_0,P) {\mbo... ...mbox{\tt :-}}} \body{parse(H,P_0,P_1),} \body{parse\_list(T,P_1,P).} \epred\epr$

Example.

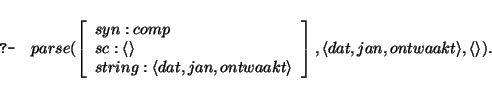
$\query{parse(\avm{ syn: comp\\ sc: \langle \rangle \\ string: \langle dat,jan,ontwaakt \rangle } ,\langle dat,jan,ontwaakt\rangle,\langle\rangle).} \equery$

The prediction step selects the lexical entry `dat'. The next goal is to show that this lexical entry is the lexical head of the top goal; furthermore the string that still has to be covered is now $\langle$ jan, ontwaakt $\rangle$ . Leaving details out the head_corner clause looks as :

$\query{head\_corner( \avm{ syn: comp\\ sc: \langle \avm{ syn: v\\ sc: \lang... ...waakt \rangle } ,} \qitem{\langle jan,ontwaakt\rangle,\langle\rangle).} \equery$
The category of dat has to be matched with the head of a rule. Notice that dat subcategorizes for a v with rule feature right. Hence the right version of the wrap predicate applies, and the next goal is to parse the v for which this complementizer subcategorizes, with input `jan, ontwaakt':

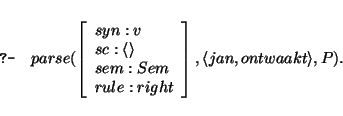
$\query{parse(\avm{ syn: v\\ sc: \langle \rangle\\ sem: Sem\\ rule: right},\langle jan,ontwaakt\rangle,P). }\equery$

Lexical lookup selects the word ontwaakt from this string. The word ontwaakt has to be shown to be the head of this v node, by the head_corner predicate:

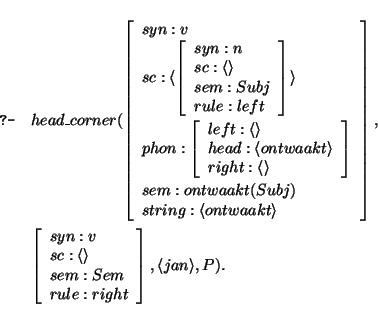
$\query{head\_corner(\avm{ syn: v\\ sc: \langle \avm{ syn: n\\ sc: \langle \r... ... \langle \rangle\\ sem: Sem\\ rule: right},\langle jan\rangle,P). } \equery$
This time the left combination rule applies and the next goal consists in parsing a NP (for which ontwaakt subcategorizes) with input string jan. This goal succeeds with an empty output string. Hence the argument of the rule has been found successfully and hence we need to connect the mother of the rule up to the v node. This succeeds trivially, instantiating the head_corner call above to:

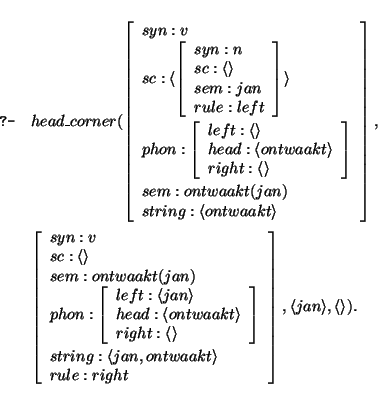
$\query{head\_corner( \avm{ syn: v\\ sc: \langle \avm{ syn: n\\ sc: \langle \... ...ontwaakt \rangle\\ rule: right}, \langle jan\rangle,\langle\rangle).} \equery$

and therefore we now have found the v for which dat subcategorizes, instantiating the parse goal above to:

$\query{parse(\avm{ syn: v\\ sc: \langle \rangle\\ sem: ontwaakt(jan)\\ pho... ...t \rangle\\ rule: right},\langle jan,ontwaak\rangle,\langle\rangle).} \equery$
Hence the next goal is to connect the complementizer with an empty subcat list up to the topgoal; again this succeeds trivially. Hence we obtain the instantiated version of the first head_corner call:

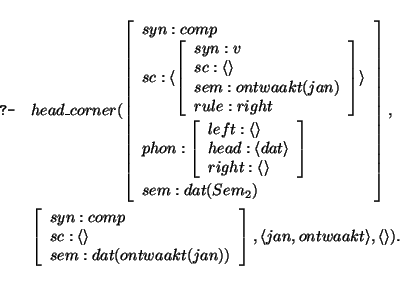
$\query{head\_corner(\avm{ syn: comp\\ sc: \langle \avm{ syn: v\\ sc: \langle... ...em: dat(ontwaakt(jan)) }, \langle jan,ontwaakt\rangle,\langle\rangle).} \equery$
and the first call to parse will succeed, yielding:

$\query{parse(\avm{ syn: comp\\ sc: \langle \rangle \\ sem: dat(ontwaakt(jan)... ...n, ontwaakt \rangle},\langle dat,jan,ontwaakt\rangle,\langle\rangle). }\equery$

The flow of control of the parsing process for this example is shown in figure 6.

**Figure 6:** Parsing `dat jan ontwaakt'
$\begin{figure} \begin{Tree} \node{\type{text}\external\cntr{dat,comp[v]}} \node{... ...}} \put(204,530){\bf 10}\put(200,557){\vector(0,1){0}} \end{picture}\end{figure}$