9.2 Terms with a Special Notation
Sometimes terms look different to us, but Prolog regards them as identical. For example, when we compare a and ’a’ , we see two distinct strings of symbols, but Prolog treats them as the same. And in fact there are many other cases where Prolog regards two strings as being exactly the same term. Why? Because it makes programming more pleasant. Sometimes the notation Prolog likes isn’t as user-friendly as the notation we would choose. So it is nice to be able to write programs in the notation we find natural, and to let Prolog run them in the notation it prefers.
Arithmetic terms
The arithmetic predicates introduced earlier are a good example of this. As was mentioned in Chapter 5 , + , - , * , and / are functors , and arithmetic expressions such as 2+3 are terms . And this is not an analogy. Apart from the fact that it can evaluate them with the help of the is/2 predicate, Prolog views strings of symbols such as 2+3 as being identical with ordinary complex terms. The following queries make this clear:
yes
?- +(2,3) == 2+3.
yes
?- 2-3 == -(2,3).
yes
?- *(2,3) == 2*3.
yes
?- 2*(7+2) == *(2,+(7,2)).
yes
In short, the familiar arithmetic notation is there for our convenience. Prolog doesn’t regard it as different from the usual term notation.
Similar remarks to the arithmetic comparison predicates < , =< , =:= , =\= , > and >= :
yes
?- (2 =< 3) == =<(2,3).
yes
?- (2 =:= 3) == =:=(2,3).
yes
?- (2 =\= 3) == =\=(2,3).
yes
?- (2 > 3) == >(2,3).
yes
?- (2 >= 3) == >=(2,3).
yes
These example show why it’s nice to have the user-friendly notation (would you want to have to work with expressions like =:=(2,3) ?). Note, by the way, that we enclosed the left hand arguments in brackets. For example, we didn’t ask
we asked
Why? Well, Prolog finds the query 2 =:= 3 == =:=(2,3) confusing, and let’s face it, can you blame it? It’s not sure whether to bracket this expression as (2 =:= 3) == =:=(2,3) (which is what we want), or as 2 =:= (3 == =:=(2,3)) . So we need to state the grouping explicitly.
One final remark. We have now introduced three rather similar looking symbols, namely = , == , and =:= (and indeed, there are also \= , \== , and =\= ). Here’s a summary:
| = | The unification predicate. |
| Succeeds if it can unify its arguments, fails otherwise. | |
| \= | The negation of the unification predicate. |
| Succeeds if = fails, and vice-versa. | |
| == | The identity predicate. |
| Succeeds if its arguments are identical, fails otherwise. | |
| \== | The negation of the identity predicate. |
| Succeeds if == fails, and vice-versa. | |
| =:= | The arithmetic equality predicate. |
| Succeeds if its arguments evaluate to the same integer. | |
| =\= | The arithmetic inequality predicate. |
| Succeeds if its arguments evaluate to different integers. |
Lists as terms
Lists are another good example of Prolog working with one internal representation, while giving us another, more user-friendly, notation to work with. Let’s start with a quick look at the user-friendly list notation it provides (that is, the square brackets [ and ] ). In fact, because Prolog also offers the | constructor, there are many ways of writing the same list, even at the user-friendly level:
yes
?- [a,b,c,d] == [a,b|[c,d]].
yes
?- [a,b,c,d] == [a,b,c|[d]].
yes
?- [a,b,c,d] == [a,b,c,d|[]].
yes
But how does Prolog view lists internally? In fact, it sees lists as terms which are built out of two special terms, namely [] , which represents the empty list, and “ . ” (the full-stop), a functor of arity 2 which is used to build non-empty lists. The terms [] and . are called list constructors.
This is how these constructors are used to build lists. Needless to say, the definition is recursive:
- The empty list is the term [ ]. It has length 0.
- A non-empty list is any term of the form . ( term , list ), where term is any Prolog term, and list is any list. If list has length n , then . ( term , list ) has length n + 1.
Let’s make sure we fully understand this definition by working our way through a few examples.
yes
?- .(f(d,e),[]) == [f(d,e)].
yes
?- .(a,.(b,[])) == [a,b].
yes
?- .(a,.(b,.(f(d,e),[]))) == [a,b,f(d,e)].
yes
?- .(.(a,[]),[]) == [[a]].
yes
?- .(.(.(a,[]),[]),[]) == [[[a]]].
yes
?- .(.(a,.(b,[])),[]) == [[a,b]].
yes
?- .(.(a,.(b,[])),.(c,[])) == [[a,b],c].
yes
?- .(.(a,[]),.(b,.(c,[]))) == [[a],b,c].
yes
?- .(.(a,[]),.(.(b,.(c,[])),[])) == [[a],[b,c]].
yes
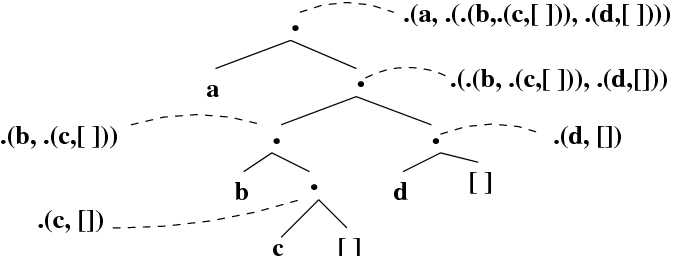
Prolog’s internal notation for lists is not as user-friendly as the use of the square bracket notation. But it’s not as bad as it seems at first sight. In fact, it works similarly to the | notation. It represents a list in two parts: its first element (the head), and a list representing the rest of the list (the tail). The trick is to read these terms as trees . The internal nodes of this tree are labeled with . and all have two daughter nodes. The subtree under the left daughter represents the first element of the list and the subtree under the right daughter represents the rest of the list. For example, the tree representation of .(a,.(.(b,.(c,[])),.(d,[]))) , that is, [a, [b,c], d] , looks like this:
One final remark. Prolog is very polite. Not only are you free to talk to it in the user-friendly notation, it will reply in the same way: